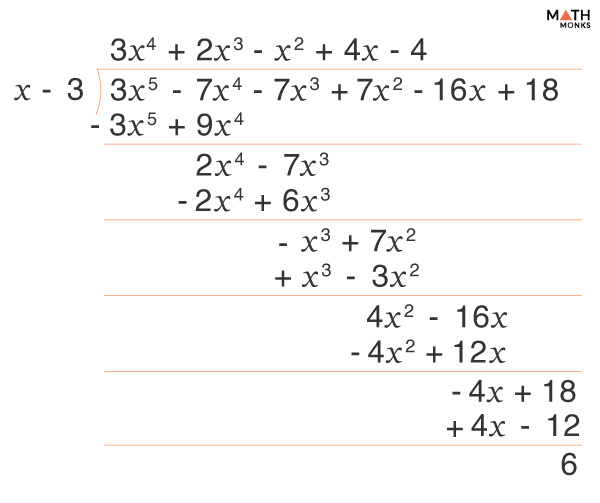Remainder Theorem

The Remainder Theorem states that if a polynomial f(x) of degree n (≥ 1) is divided by a linear polynomial (a polynomial of degree 1) g(x) of the form (x – a), the remainder of this division is the same as the value obtained by substituting r(x) = f(a) into the polynomial f(x).

Mathematically,

If f(x) = (x – a) × q(x) + r(x), then r(x) = f(a)

For example, if we divide the number 15 by 2, we get 7 as the quotient and 1 as the remainder.

Here, the dividend 15 can be written as:

Dividend = divisor × quotient + remainder ⇒ 15 = 2 × 7 + 1

Similarly, on dividing a polynomial f(x) of degree n ≥ 1 by a linear polynomial g(x), we get the quotient q(x) and the remainder r(x).

Here, we can write,

Dividend = divisor × quotient + remainder ⇒ f(x) = g(x) × q(x) + r(x), where the remainder r(x) can be found by long division, synthetic division, or by using the remainder theorem.

Proof

Substituting the value x = a in f(x) = (x – a) × q(x) + r(x), we get

f(a) = (a – a) × q(a) + r(a)

⇒ f(a) = 0 × q(a) + r(a)

⇒ f(a) = r(a)

Here, the degree of the remainder is one less than the divisor polynomial’s degree. Based on the theorem, the remainder is always constant (degree 0) as we divide f(x) by a linear polynomial. Thus, f(a) = r(a) = r(x)

Now, let us verify this with an example.

Here, we will divide the polynomial (3x⁵ – 7x⁴ – 7x³ + 7x² – 16x + 18) by (x – 3), using three possible methods.

Using Long Division

Using Synthetic Division

Using Remainder Theorem

Given, 

f(x) = 3x⁵ – 7x⁴ – 7x³ + 7x² – 16x + 18

By setting x – a = 0

⇒ x – 3 = 0

⇒ x = 3

Thus, r(x) = f(3)

f(3) = 3(3)⁵ – 7(3)⁴ – 7(3)³ + 7(3)² – 16(3) + 18 = 6

⇒ r(x) = 6

Therefore, each of the methods mentioned results in the same remainder. Yet, the process becomes more straightforward with the final method. Sometimes, the remainder is zero (also known as zero of the polynomial) when dividing a polynomial f(x) by a linear polynomial (x − a). This indicates that (x − a) is a factor of the polynomial.

Now, on expanding the theorem for different types of linear polynomials, we get

• x – a = 0 ⇒ x = a, thus, f(x) ÷ (x – a) gives r(x) = f(a)
• ax + b = 0 ⇒ ${x=\dfrac{-b}{a}}$, thus, f(x) ÷ (ax + b) gives ${r\left( x\right) =f\left( \dfrac{-b}{a}\right)}$
• ax – b = 0 ⇒ ${x=\dfrac{b}{a}}$, thus, f(x) ÷ (ax – b) gives ${r\left( x\right) =f\left( \dfrac{b}{a}\right)}$
• bx – a = 0 ⇒ ${x=\dfrac{a}{b}}$, thus, f(x) ÷ (bx – a) gives ${r\left( x\right) =f\left( \dfrac{a}{b}\right)}$ 

Remainder Theorem and Factor Theorem

A special case of the remainder theorem called the factor theorem is used when we need to find the factors of a given polynomial based on its zeros. 

Let us consider the polynomial f(x) = x² – 6x + 8 and find the remainder when x = 2 and x = -1.

Using the remainder theorem, we get 

At x = 2, r(x) = f(2) = (2)² – 6(2) + 8 = 0

At x = -1, r(x) = f(-1) = (-1)² – 6(-1) + 8 = 15

We observe f(x) = 15 for x = -1 and f(x) = 0 for x = 2. Thus, x = 2 is the zero of f(x), whereas x = -1 is not a zero of f(x).

Again, the remainder of f(x) at x = -1 is 15, and the remainder at x = 2 is 0

Thus, according to the factor theorem, (x – 2) is a factor of f(x).

Solved Examples

• More Resources
  • Chinese Remainder Theorem
  • Fermat’s Little Theorem
  • Euler’s Theorem
  • Taylor’s Theorem
  • Wilson’s Theorem
  • Quotient Remainder Theorem
  • Factor Theorem