A transcendental number is a real or complex number that is not a root of any non-zero polynomial equation with rational coefficients.
Thus, if we cannot express a number as the solution to an algebraic equation like ${a_{n}x^{n}+a_{n-3}x^{n-1}+\ldots +a_{1}x+a_{0}=0}$, where the coefficients ${a_{0},a_{1},\ldots a_{n}}$ are rational numbers, then those are transcend numbers.
The symbols ℝ ∖ 𝔸 or ℝ – 𝔸 are often used to denote real transcendental numbers, where ℝ is the set of algebraic numbers.
Transcendental numbers are irrational, but the converse is not always true, as all irrational numbers are not transcendental.
For example,
x2 – 2 = 0, which has a root x = ${\sqrt{2}}$, is an irrational and algebraic number but not a transcendental number.
History
Joseph Liouville introduced the first transcendental number, the Liouville constant, in 1844. The Liouville constant number is irrational but is not a root of any polynomial equation.
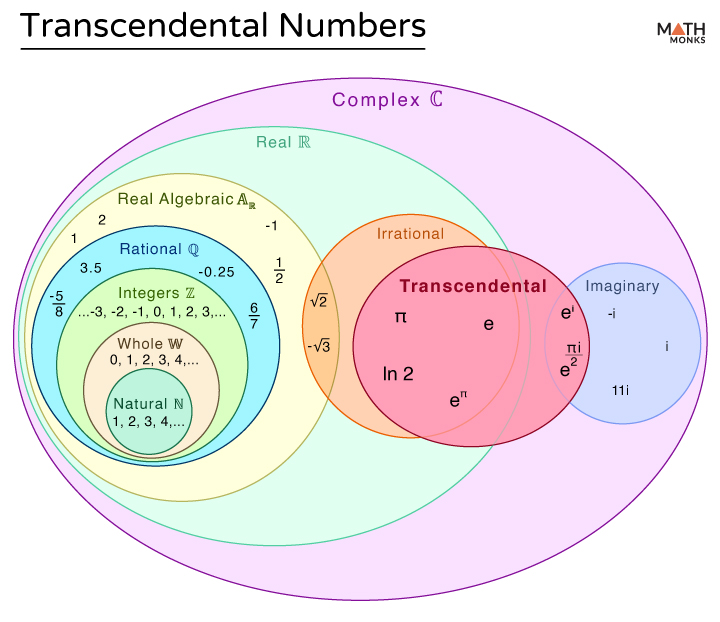
With Venn Diagram
The following Venn diagram shows the transcendental numbers in the number system:
Examples of Common Transcendental Numbers
π (Pi) = 3.1415 …: It is known for calculating the area and circumference of a circle. Ferdinand von Lindemann proved that π is not the root of any polynomial equation with rational coefficients, meaning it is impossible to square the circle exactly.
e (Euler’s Number)= 2.718 …: It is the base of the natural logarithm. Charles Hermite proved the transcendence of e in 1873. The number e is crucial in calculus, particularly in studying exponential growth and decay processes.
List
Here is a list of a few more transcendental numbers.
- Euler’s constant, gamma = 0.577215 … = ${\lim _{n\rightarrow \infty }\left( 1+\dfrac{1}{2}+\dfrac{1}{3}+\ldots +\dfrac{1}{n}-\ln \left( n\right) \right)}$
- Catalan’s constant, G = ${\sum ^{\infty }_{k=0}\dfrac{\left( -1\right) ^{k}}{\left( 2k+1\right) ^{2}}}$
- Liouville’s number = 0.110001000000000000000001000 …
- Chaitin’s constant = the probability that a random algorithm halts
- Chapernowne’s number = 0.12345678910111213141516171819202122232425…
How Many Transcendental Numbers are there?
There are uncountable such transcendental numbers. Since polynomials with rational coefficients are countable, and each polynomial has only a finite number of zeroes, it follows that algebraic numbers are also countable.
Difference Between Transcendental and Algebraic Numbers
What is then an algebraic number?
When we have a polynomial equation like x2 – 2 = 0, whose coefficients are rational, then x is an algebraic number.
Algebraic numbers, like 0, 1, 2, ${\dfrac{1}{2}}$, ${\sqrt{2}}$, are roots of polynomials with integer coefficients.
For example,
f(x) = x has root x = 0
f(x) = x – 1 has root x = 1
f(x) = x + 1 has root x = -1
f(x) = 2x + 1 has root x = ${-\dfrac{1}{2}}$
f(x) = x2 – 2 has a root x = ${\sqrt{2}}$
Thus, all integers, rational numbers, and some irrational numbers (such as ${\sqrt{2}}$) are algebraic. Some polynomial f(x) with integer coefficients exists for these algebraic numbers where f(a) = 0.
Again, transcendental numbers do not satisfy any such polynomial equation. For a transcendental number ‘t,’ there is no f(t) where f(t)=0.
For example,
${2^{\sqrt{3}}}$ is transcendental, which means there is no polynomial f(x) with integer coefficients for which ${f\left( 2^{\sqrt{3}}\right) =0}$
Thus, it is unusual to find a number that is not algebraic. However, a lot of such numbers exist.
Moreover, algebraic and transcendental together combine to form a set of real numbers. Since algebraic numbers can be arranged in one-to-one correspondence with whole numbers, they are countable. Also, real numbers are uncountable, and thus, transcendental numbers must be uncountable.
Hence, many more Transcendental numbers exist than algebraic numbers, and most real numbers are transcendental. This argument also applies to complex numbers.
Proving eα and ab Transcendental
Proving a number to be transcendental involves showing that it does not satisfy any algebraic equation with rational coefficients. The proofs typically use complex analysis, number theory, and algebra.
eα by Lindemann–Weierstrass Theorem
The Lindemann–Weierstrass Theorem states that if α1,α2, …, αn are distinct non-zero algebraic numbers, then the numbers ${e^{\alpha _{1}},e^{\alpha _{2}},\ldots ,e^{\alpha _{n}}}$ are linearly independent over the field algebraic numbers.
Thus, ${e^{\alpha _{1}},e^{\alpha _{2}},\ldots ,e^{\alpha _{n}}}$ are transcendental.
ab by Gelfond–Schneider Theorem
The Gelfond–Schneider Theorem states that if a and b are algebraic numbers, with a ≠ 0, 1, and b is irrational, then ab is transcendental.
This is used to prove the transcendence of numbers like ${2^{\sqrt{2}}}$ and ${\sqrt{2}^{\sqrt{2}}}$
Transcendental Function is Not Algebraic
Just as a transcendental number, a transcendental function is also not algebraic. It is a function that cannot be constructed from elementary functions and their inverses in a finite number of steps.
An example is the sine function, sin(x).