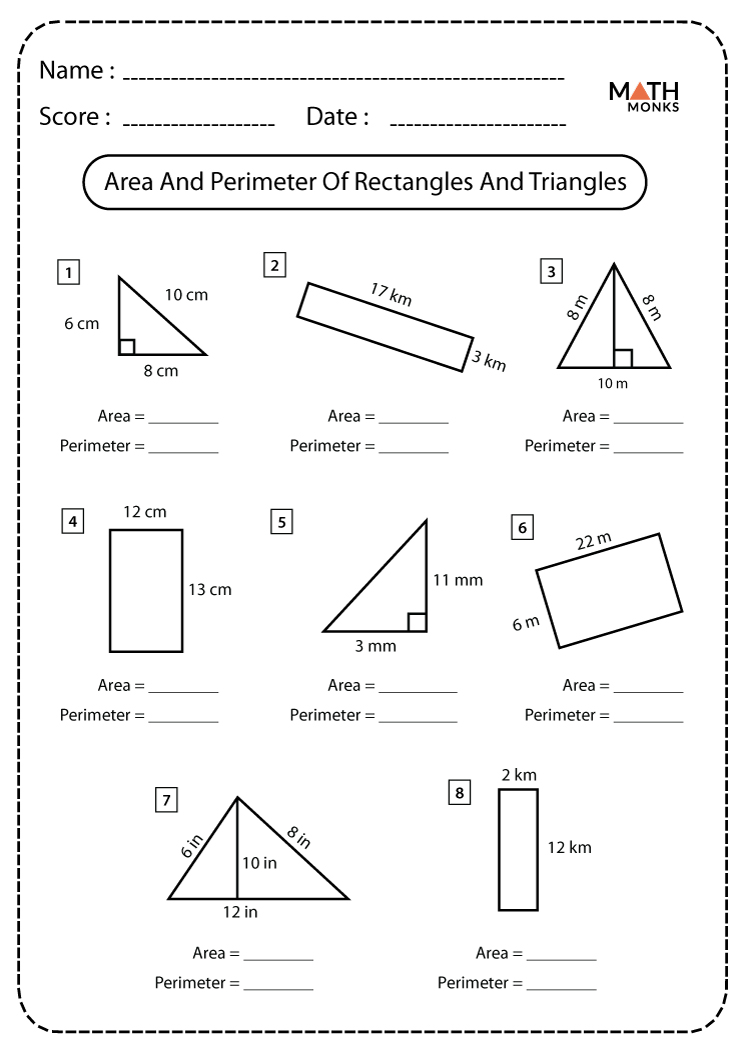
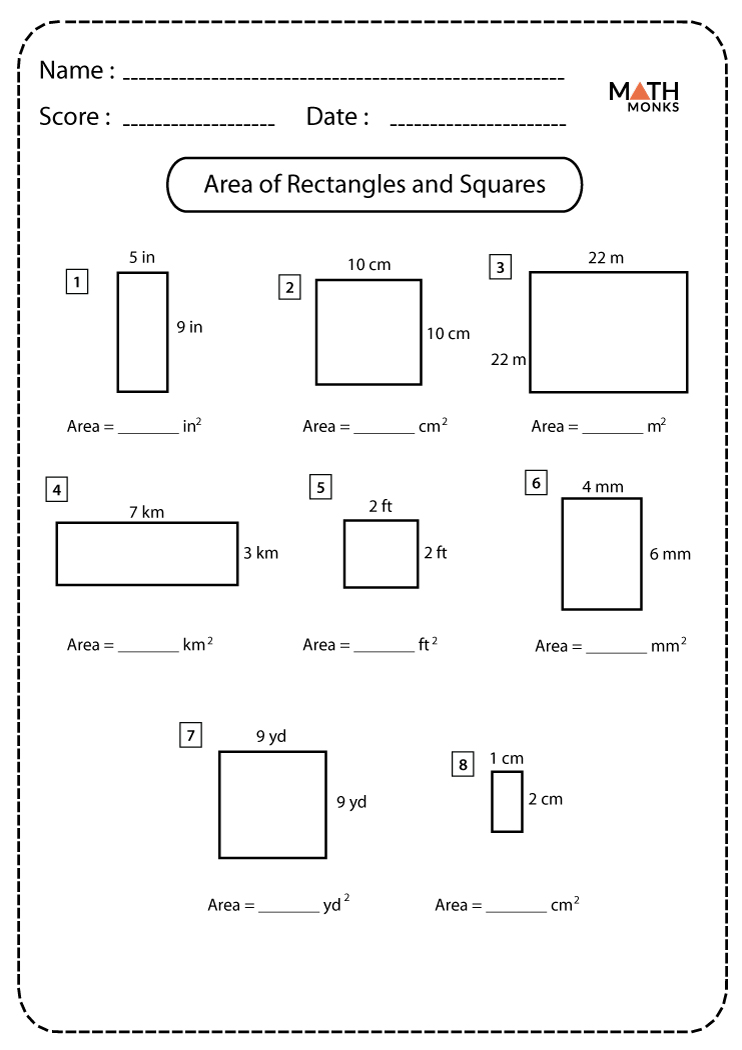
Definition
A plane figure with four straight sides making four right
internal angles.
Rectangle
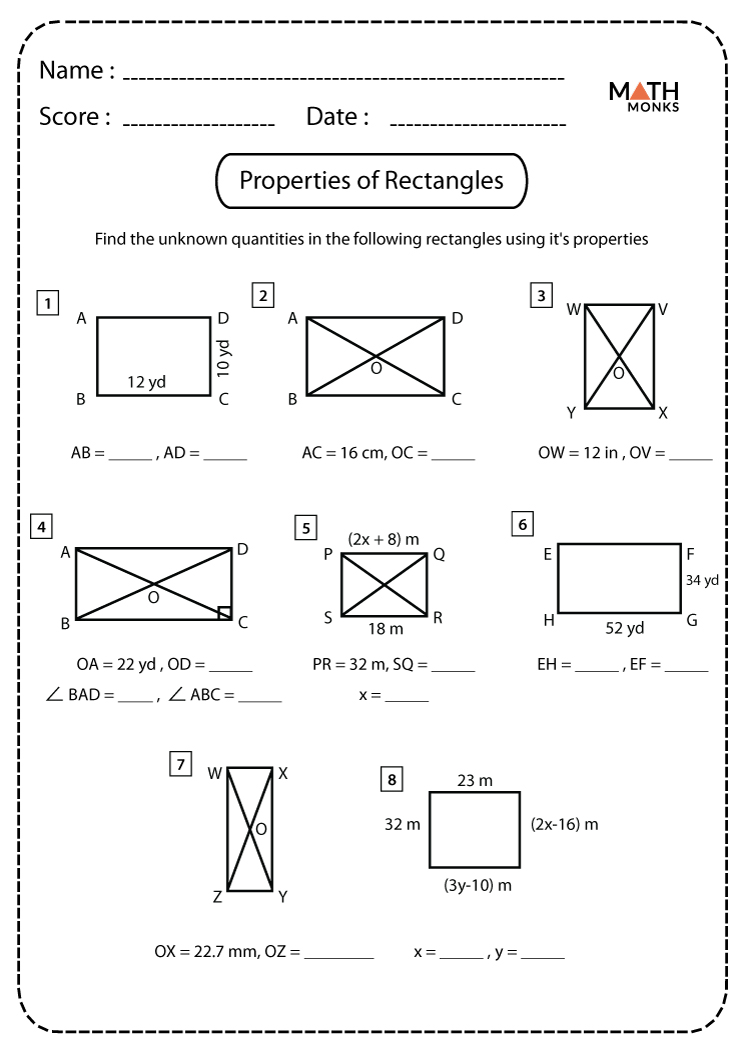
Properties
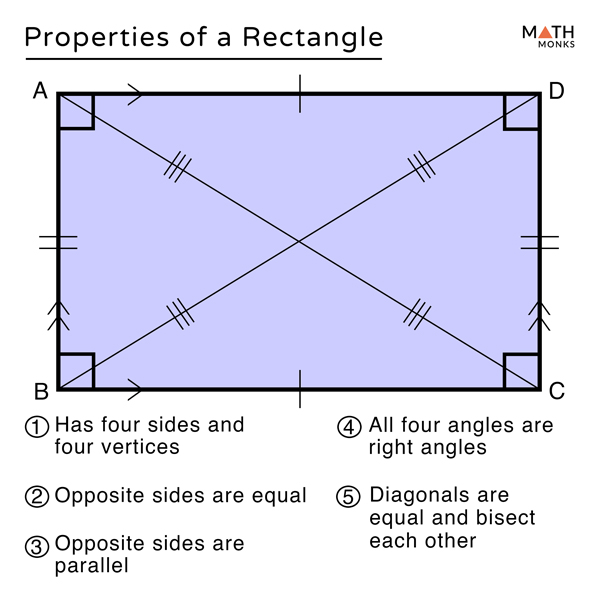Properties of a Rectangle
- Has four sides and four angles; in ▭ ABCD, AB, BC, CD, and DA are four sides and ∠ABC, ∠BCD, ∠CDA, ∠DAB are four angles
- Opposite sides are equal; so AB = CD and BC= DA
- Opposite sides are parallel; AB ∥ CD and BC ∥ DA
- All the angles are 90°; in ▭ ABCD, ∠ABC = ∠BCD = ∠CDA =∠DAB = 90°
- The diagonals are equal and bisect each other; so AC = BD
- The sum of the interior angles is equal to 360 degrees; ∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
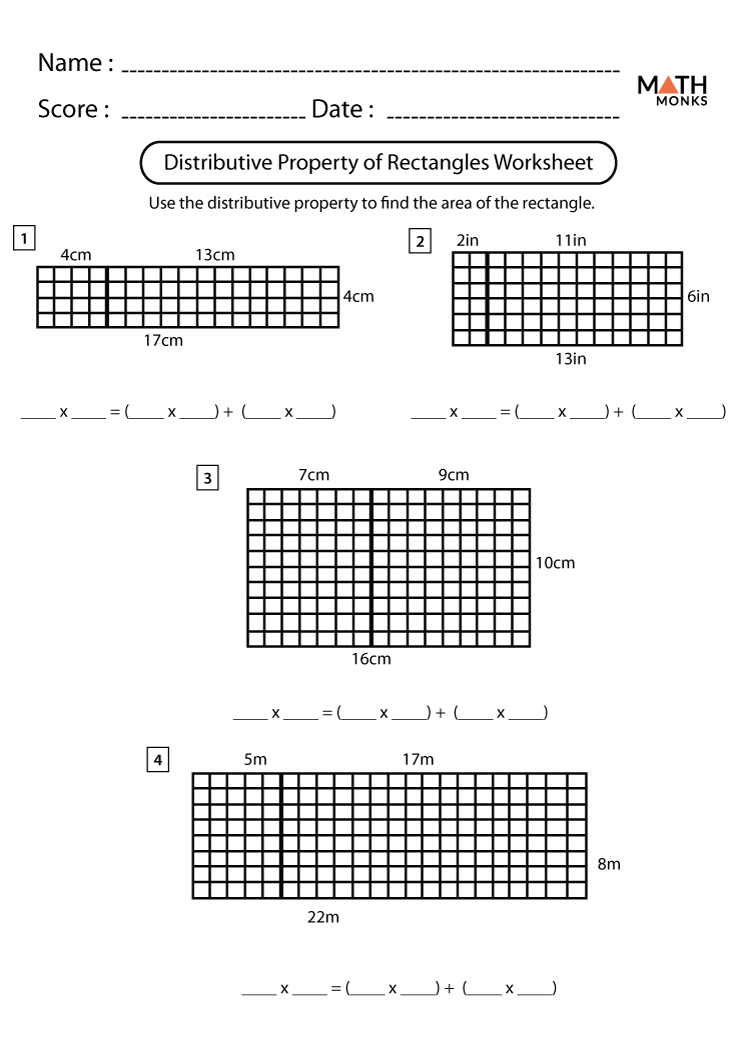
Formulas
The line segments linking opposite vertices or corners of the rectangle. The formula is given below:
Diagonal (D) = √w2 + l2, here w = width, l = length
Problem: Finding the diagonal of a rectangle when the WIDTH and LENGTH are known
![]()
Find the diagonal of a rectangle whose width is 12 cm and length is 5 cm.
![]()
Solution:
As we know,
Diagonal (d ) = √(w 2 + l 2), where w = 12 cm and l = 5 cm
= √(122 + 52)
=√(144 + 25)
= √169
= 13 cm
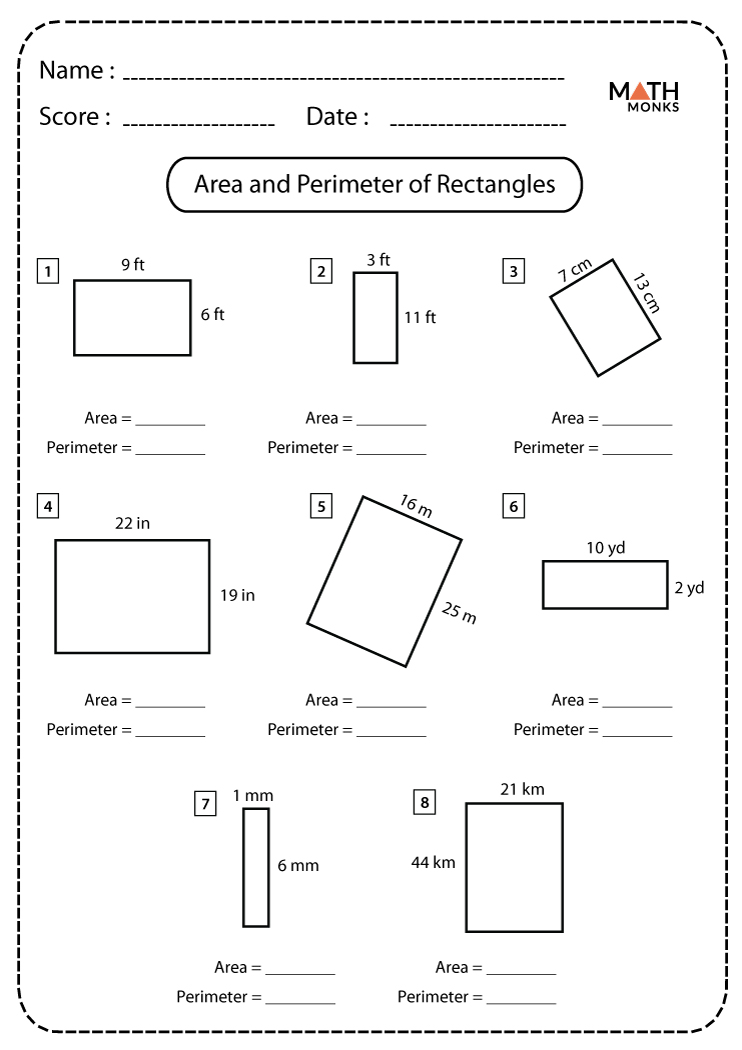
The total space enclosed by the rectangle. The formula is given below:
Area (A) = w × l, here w = width, l = length
Problem: Finding the area of a rectangle when the WIDTH and LENGTH are known
![]()
Find the area of a rectangle whose width is 10 cm and length is 6 cm.
![]()
Solution:
As we know,
Area (A) = w × l, where w = 10 cm and l = 6 cm
= 10 × 6 cm
= 60 cm2
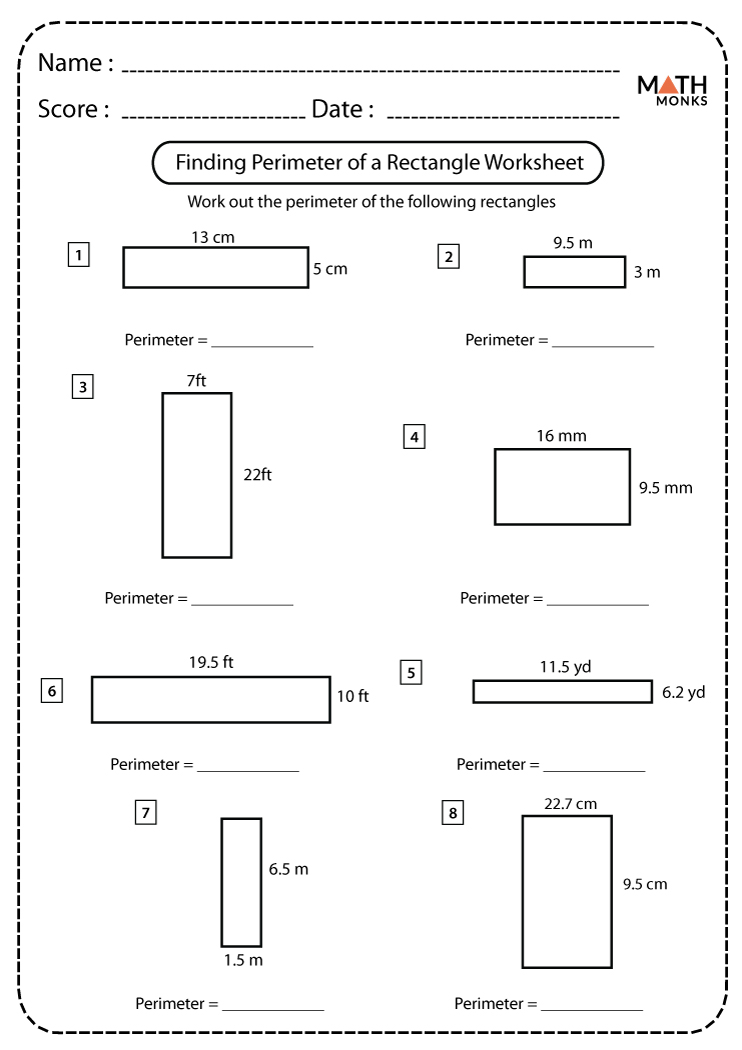
The total distance covered around the edge of the rectangle. The formula is given below:
Perimeter (P) = 2(w + l), here w = width, l = length
Problem: Finding the perimeter of a rectangle when the WIDTH and LENGTH are known
![]()
Find the perimeter of a rectangle whose width is 7 cm and length is 9 cm.
![]()
Solution:
As we know,
Perimeter (P ) = 2 (w + l ), wherew = 7 cm and l = 9 cm
= 2(7 + 9) cm
= 2 × 16 cm
= 32 cm
