Fractions represent a part of the whole. It represents the number of parts of a certain number, size, or collection compared to the total number of equal parts.
Notation
A number is written in the fractional form as ${\dfrac{a}{b}}$
⇒ ${\dfrac{Numerator}{Denominator}}$
Examples
If a pizza is cut into ten equal slices and one slice of the pizza is placed on a dish, then each dish is said to have ${\dfrac{1}{10}}$ of the pizza. It is read as ‘one-tenth’ or ‘1 by 10.’
Here are some more real-life examples involving fractions:
- Dividing a cake into 5 equal parts means each part is ${\dfrac{1}{5}}$ of the whole.
- If the traveling time from your home to the office is 30 minutes, it means ‘half an hour’ is taken, which is written as ${\dfrac{1}{2}}$.
- Test scores are often represented as fractions, like ${\dfrac{9}{10}}$ or ${\dfrac{48}{50}}$.
- Food recipes use fractions, such as ${\dfrac{1}{4}}$ teaspoon of sugar or ${\dfrac{1}{2}}$ tablespoon of salt.
Parts
A fraction consists of two main parts: a numerator and a denominator, separated by a horizontal bar known as the fraction bar.
Numerator
The numerator is the top number above the fraction bar, indicating how many parts we have.
Denominator
The denominator is the number below the fraction bar, which shows how many equal parts the whole is divided into.
The diagram below shows the different parts of the fraction ${\dfrac{1}{10}}$.
Representing a Fraction
A fraction can be represented in three ways: a fraction, a percentage, or a decimal.
Fractional Form
It is the most common form of representing fractions. A fraction in fractional form is denoted in ${\dfrac{p}{q}}$ form, where p is the numerator, q is the denominator, and they are separated by a fraction bar.
Example
${\dfrac{1}{10}}$ represents 1 part out of 10 equal parts of a whole. Here, the numerator is 1, and the denominator is 10
Decimal Form
In this form, the fraction is represented as a decimal number.
Example
The fraction ${\dfrac{1}{10}}$ can be written in decimal form by dividing the numerator (1) by the denominator (10), which gives 0.1
Percentage Form
The fraction can also be represented as a percentage by multiplying the fraction by 100.
Example
The fraction ${\dfrac{1}{10}}$ is multiplied by 100
${\dfrac{1}{10}\times 100=10\%}$
Thus, ${\dfrac{1}{10}}$ is percentage form is 10%
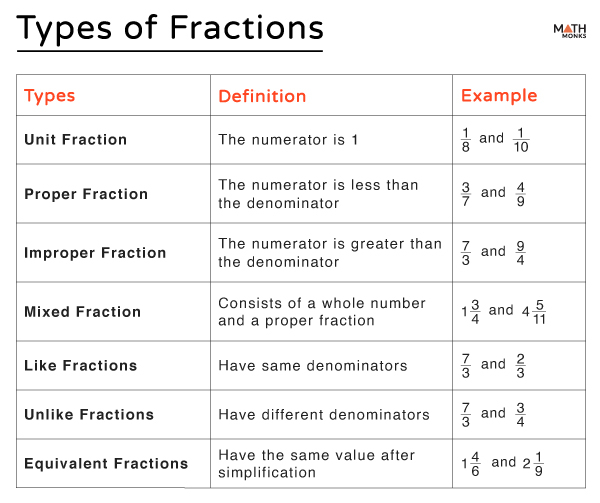
Types
Fractions can be classified into several types:
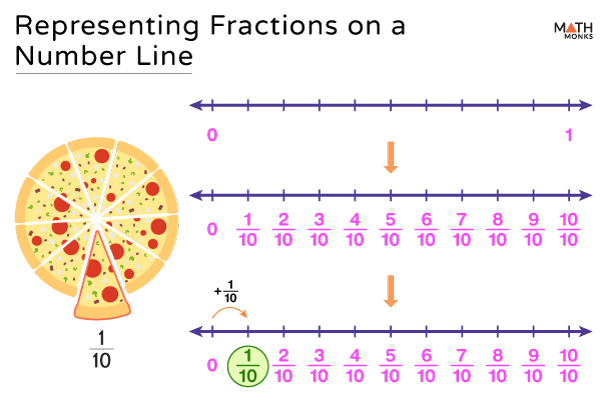
On a Number Line
A number line is a useful tool for visualizing fractions. Let us express ${\dfrac{1}{10}}$ on the number line.
- Drawing a horizontal line: This line represents the number line.
- Marking whole numbers: We then divide the number line into whole numbers (here, 0 and 1) by placing points at equal intervals based on the denominator of the given fraction.
- Dividing the Intervals: We further divide the interval of whole numbers into equal parts based on the denominator. Here, we will divide the number line between 0 and 1 into 10 equal parts. The first interval is marked as ${\dfrac{1}{10}}$, the second is ${\dfrac{2}{10}}$, and so on, with the last mark being ${\dfrac{10}{10}}$, or 1.
- Plotting the fraction: The fraction is finally plotted by marking a point on the number line corresponding to the numerator.
Here is the number line.
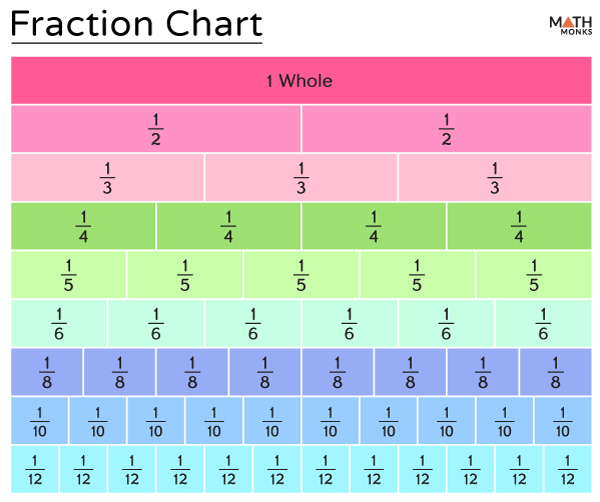
Here is a printable chart for visualizing equivalent fractions.
Properties
Here are some properties used to simplify problems involving fractions.
- Commutative and associative properties hold for addition and multiplication of fractions
- Fractions obey the distributive law of multiplication over addition
- The identity element is 0 for fractional addition and 1 for fractional multiplication
- The multiplicative inverse of ${\dfrac{a}{b}}$ is ${\dfrac{b}{a}}$, where a and b are non-zero elements
Simplifying
Simplifying a fraction means to reduce the fraction to its simplest form. To simplify, we divide the numerator and denominator by the greatest common factor (GCF).
Let us simplify ${\dfrac{20}{30}}$
The GCF of 20 and 30 is 10
Now, by dividing the numerator and denominator by 10, we get
${\dfrac{20}{30}}$
= ${\dfrac{2}{3}}$
Adding and Subtracting
With Same Denominators
To add or subtract fractions with the same denominator, we follow the following steps:
Let us add ${\dfrac{7}{3}}$ and ${\dfrac{2}{3}}$
Step 1: Adding/subtracting the numerators together
${\dfrac{7}{3}+\dfrac{2}{3}}$
= ${\dfrac{7+2}{3}}$
Step 2: Simplifying
= ${\dfrac{9}{3}}$
= ${3}$
Now, if we subtract the fraction ${\dfrac{2}{3}}$ from ${\dfrac{7}{3}}$, then
${\dfrac{7}{3}-\dfrac{2}{3}}$
= ${\dfrac{7-2}{3}}$
= ${\dfrac{5}{3}}$
With Different Denominators
We follow the given steps to add or subtract fractions with different denominators.
Let us add ${\dfrac{1}{2}+\dfrac{3}{4}}$
Step 1: Finding the LCM of the denominators
Here, the denominators are 2 and 4
The LCM of 2 and 4 is 4
Step 2: Rationalizing the denominators
Now, for rationalizing, we will multiply the first fraction by 2 and the second fraction by 1
${\dfrac{1\times 2}{2\times 2}+\dfrac{3\times 1}{4\times 1}}$
= ${\dfrac{2}{4}+\dfrac{3}{4}}$, the fractions with the same denominators.
Step 3: Adding the numerators together
= ${\dfrac{2+3}{4}}$
Step 4: Simplifying
= ${\dfrac{5}{4}}$
= ${1\dfrac{1}{4}}$
Multiplying and Dividing
Multiplying
While multiplying fractions, we multiply all the numerators and all the denominators together.
On multiplying ${\dfrac{p}{q}}$ and ${\dfrac{r}{s}}$
${\dfrac{a}{b}\times \dfrac{c}{d}}$
= ${\dfrac{ac}{bd}}$
For example,
${\dfrac{3}{7}\times \dfrac{5}{11}}$
= ${\dfrac{3\times 5}{7\times 11}}$
= ${\dfrac{15}{77}}$
Dividing
While dividing the fractions, we multiply the first fraction by the reciprocal of the second fraction.
For example,
${\dfrac{3}{7}\div \dfrac{5}{11}}$
= ${\dfrac{3}{7}\times \dfrac{11}{5}}$
= ${\dfrac{3\times 11}{7\times 5}}$
= ${\dfrac{33}{35}}$
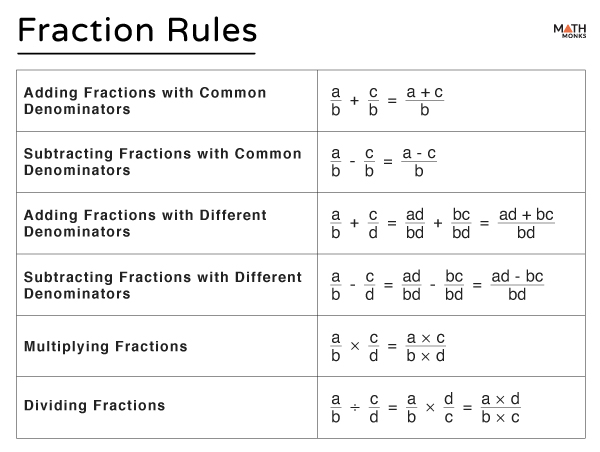
Fraction Rules Summary
Here is a summary of the rules we follow for simplifying fractions.
Solved Examples
![]()
From the given fractions, determine the proper and improper fractions.
${\dfrac{1}{15}}$, ${\dfrac{3}{8}}$, ${\dfrac{9}{2}}$, ${\dfrac{11}{17}}$, ${\dfrac{13}{3}}$, ${\dfrac{7}{11}}$, ${\dfrac{4}{8}}$, and ${\dfrac{3}{2}}$
Solution:
![]()
Here,
The proper fractions are ${\dfrac{1}{15}}$, ${\dfrac{3}{8}}$, ${\dfrac{11}{17}}$, ${\dfrac{7}{11}}$, and ${\dfrac{4}{8}}$
The improper fractions are ${\dfrac{9}{2}}$, ${\dfrac{13}{3}}$, and ${\dfrac{3}{2}}$
![]()
In a class of 60 students, ${\dfrac{1}{5}}$ of them went on a family trip during their summer break. How many students went on a trip?
Solution:
![]()
Here, the total number of students is 60
As we know,
The number of students who went on a family trip is ${\dfrac{1}{5}}$ of the total number of students.
Thus, the number of students who went on a trip
= ${\dfrac{1}{5}}$ of 60
= ${\dfrac{1}{5}\times 60}$
= ${12}$
