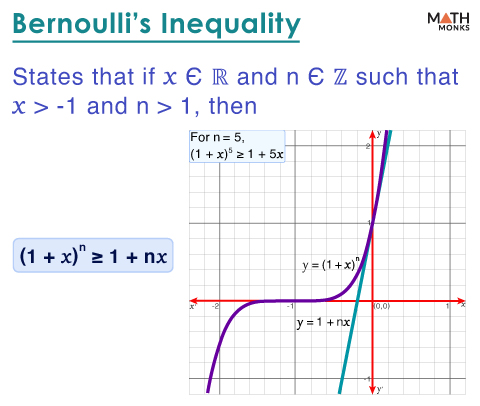
Bernoulli’s inequality (named after Jacob Bernoulli) approximates exponentiations of (1 + x) or more simply gives the approximation of (1 + x)n.
Mathematically, the inequality is written as:
(1 + x)n ≥ 1 + nx, here ‘x’ is any real number greater than -1, and ‘n’ is any integer greater than 1
It is used to prove the convergence of sequences and series, providing an upper bound to show that the sequence converges to a particular limit and solves the critical limit problems easily.
Proof
Let us prove Bernoulli’s inequality using the process of mathematical induction.
Base Step
For n = 0, (1 + x)0 = 1 ≥ 1 + 0 ⋅ x, true
Inductive Step
Let us consider (1 + x)k ≥ 1 + kx, for any integer n = k (> -1)
Now, assuming n = k + 1, we get
(1 + x)k + 1 = (1 + x)k ⋅ (1 + x) ≥ (1 + kx) ⋅ (1 + x)
⇒ (1 + x)k + 1 ≥ (1 + kx) ⋅ (1 + x)
⇒ (1 + x)k + 1 ≥ 1 + kx + x + kx2
⇒ (1 + x)k + 1 ≥ 1 + (k + 1)x + kx2 ≥ 1 + (k + 1)x
⇒ (1 + x)k + 1 ≥ 1 + (k + 1)x
Thus, (1 + x)n ≥ 1 + nx, for any integer greater than -1
Hence, Bernoulli’s inequality is proved.
Alternate Proof
We can also prove Bernoulli’s inequality using the binomial theorem.
Case 1:
For x > 0, ${\left( 1+x\right) ^{n}=1+nx+\begin{pmatrix} n \\ 2 \end{pmatrix}x^{2}+\begin{pmatrix} n \\ 3 \end{pmatrix}x^{3}+\ldots +\begin{pmatrix} n \\ n \end{pmatrix}x^{n}\geq 1+nx}$ …..(i)
Case 2:
For x = 0, (1 + x)n ≥ 1 + nx, which is trivially true.
Case 3:
For -1 < x < 0, we consider y = -x, then 0 < y < 1, and we have
${\left( 1-y\right) ^{n}=1-ny+\begin{pmatrix} n \\ 2 \end{pmatrix}y^{2}-\begin{pmatrix} n \\ 3 \end{pmatrix}y^{3}+\ldots +\left( -1\right) ^{n}\begin{pmatrix} n \\ n \end{pmatrix}y^{n}}$ …..(ii)
Putting y = 0, we get
${0=\left( 1-1\right) ^{n}=1-n+\begin{pmatrix} n \\ 2 \end{pmatrix}-\begin{pmatrix} n \\ 3 \end{pmatrix}+\ldots +\left( -1\right) ^{n}\begin{pmatrix} n \\ n \end{pmatrix}}$
⇒ ${\begin{pmatrix} n \\ 2 \end{pmatrix}-\begin{pmatrix} n \\ 3 \end{pmatrix}+\ldots +\left( -1\right) ^{n}\begin{pmatrix} n \\ n \end{pmatrix}=n-1 >0}$ …..(iii)
Since 0 < y < 1, y2 > y3 > … > yn
Now, multiplying each term of (ii) by a factor that is smaller than its previous term, we get
${\begin{pmatrix} n \\ 2 \end{pmatrix}y^{2}-\begin{pmatrix} n \\ 3 \end{pmatrix}y^{3}+\ldots +\left( -1\right) ^{n}\begin{pmatrix} n \\ n \end{pmatrix}y^{n}\geq 0}$ …..(iv)
From (ii), (1 – y)n ≥ 1 – ny, for 0 < y < 1
⇒ (1 + x)n ≥ 1 + nx, for -1 < x < 0
Thus, Bernoulli’s inequality is proved.
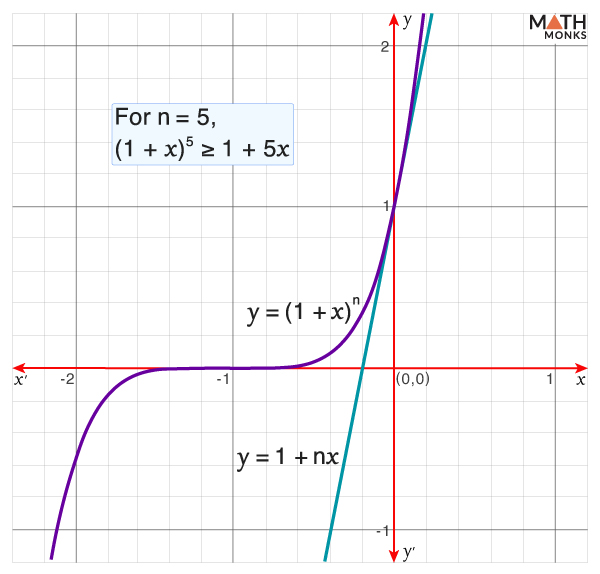
Graphical Representation
To verify Bernoulli’s inequality, here, we will plot the graphs of y = (1 + x)n and y = 1 + nx, for n = 5.
Solved Example
![]() Use Bernoulli’s inequality to prove ${\dfrac{2n+3}{2n}\geq \left( \dfrac{5}{2}\right) ^{\dfrac{1}{n}}}$
Use Bernoulli’s inequality to prove ${\dfrac{2n+3}{2n}\geq \left( \dfrac{5}{2}\right) ^{\dfrac{1}{n}}}$
Solution:
![]()
As we know, Bernoulli’s inequality states:
(1 + x)n ≥ 1 + nx, where x Є ℝ, n Є ℤ such that x > -1 and n > 1
Here, substituting x = ${\dfrac{3}{2n}}$ in Bernoulli’s inequality, we get
${\left( 1+\dfrac{3}{2n}\right) ^{n}\geq 1+n\times \dfrac{3}{2n}}$
⇒ ${\left( 1+\dfrac{3}{2n}\right) ^{n}\geq 1+\dfrac{3}{2}}$
⇒ ${\left( 1+\dfrac{3}{2n}\right) ^{n}\geq \dfrac{5}{2}}$
Taking the nth root of both sides, we get
${\left( 1+\dfrac{3}{2n}\right) \geq \left( \dfrac{5}{2}\right) ^{\dfrac{1}{n}}}$
⇒ ${\left( \dfrac{2n+3}{2n}\right) \geq \left( \dfrac{5}{2}\right) ^{\dfrac{1}{n}}}$
Thus, the given inequality is proved.