Modular Arithmetic

Modular arithmetic, also known as clock arithmetic, deals with finding the remainder when one number is divided by another number. It involves taking the modulus (in short, ‘mod’) of the number used for division. 

If ‘A’ and ‘B’ are two integers such that  ‘A’ is divided by ‘B,’ then:

${\dfrac{A}{B}=Q,remainderR}$

Here,

• Dividend = A
• Divisor = B
• Quotient = Q, and 
• Remainder = R

In modular arithmetic, it is written as A mod B = R, read as ‘A modulo B equals R’ where ‘B’ is referred to as modulus. This means if we divide ‘A’ by ‘B’ the remainder is ‘R.’

For example, ${\dfrac{14}{3}=4,remainder2}$ ⇒ 14 mod 3 = 2, which means if 14 is divided by 3, the remainder is 2.

The concept of modular arithmetic can be best explained using the face of a clock. It has many applications in fields like cryptography, computer science, and number theory, and it is often used to detect errors in identification numbers. 

Visualizing Modulus with a Clock

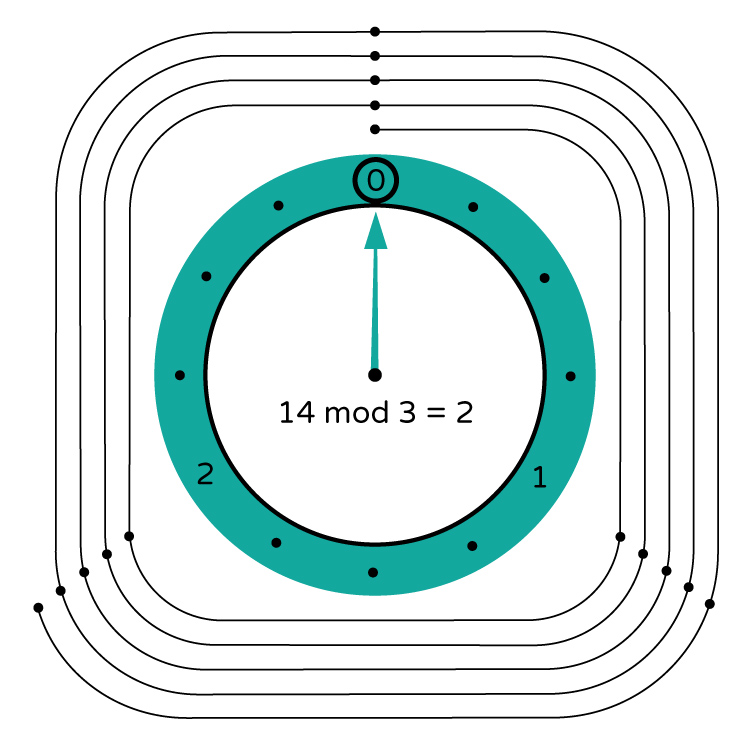
Now, let us visualize the modulo operator with a clock. To find the result of 14 mod 3 (A mod B), we will follow the following steps:

Step 1: Constructing the clock for size ‘B’

First, we write 0 at the top of the clock and continue clockwise by writing 1, 2, … up to one less than the modulus. Here, 14 mod 3, the modulus is 3. Thus, 12 is replaced by a 0, then continuing 1 and 2 (= 3 – 1) in the clockwise direction of the circle, which is for the modulus of 3.

Step 2: Starting at 0 and moving around the clock for ‘A’ steps

Here, we start from 0, increase the number by 1 in each step, and divide them by 3. This continues until the number reaches one less than the number we are dividing by. After that, the sequence repeats.

On dividing by 3, we get

• ${\dfrac{0}{3}=0,remainder0}$
• ${\dfrac{1}{3}=0,remainder1}$
• ${\dfrac{2}{3}=0,remainder2}$
• ${\dfrac{3}{3}=1,remainder0}$
• ${\dfrac{4}{3}=1,remainder1}$
• ${\dfrac{5}{3}=1,remainder2}$
• ${\dfrac{6}{3}=2,remainder0}$
• ${\dfrac{7}{3}=2,remainder1}$
• ${\dfrac{8}{3}=2,remainder2}$
• ${\dfrac{9}{3}=3,remainder0}$
• ${\dfrac{10}{3}=3,remainder1}$
• ${\dfrac{11}{3}=3,remainder2}$
• ${\dfrac{12}{3}=4,remainder0}$
• ${\dfrac{13}{3}=4,remainder1}$
• ${\dfrac{14}{3}=4,remainder2}$

Step 3: Finding the Solution

Thus, we get the solution 2. 

Congruence Modulo

Two integers, ‘A’ and ‘B,’ are considered congruent under modulo ‘n’ if they yield the same remainder when divided by the positive integer ‘n.’

For example, 

17 and 32 are congruent to modulo 3, which implies 17 ≡ 32 (mod 3). This means the remainder of dividing ‘17 by 3’ and ‘32 by 3’ are 2. 

In general, two integers, ‘A’ and ‘B,’ are congruent to modulo ‘n’ when (A – B) is a multiple of ‘n,’ which means A ≡ B when ${\dfrac{A-B}{n}}$ is an integer. However, A ≢ B (mod n) means that ‘A’ and ‘B’ are not congruent to modulo ‘n.’ 

Rules

While solving modular arithmetic problems, we directly operate on the remainder without tedious computations, following the given rules or properties.

Addition

• If A + B = C, then A (mod n) + B (mod n) ≡ C (mod n)
• If A ≡ B (mod n), then A + k ≡ B + k (mod n) for any integer ‘k’
• If A ≡ B (mod n) and C ≡ D (mod n), then A + C ≡ B + D (mod n)
• If A ≡ B (mod n), then -A ≡ -B (mod n)

Subtraction

The same rules for modular addition can also be applied to modular subtraction.

Multiplication

• If A ⋅ B = C, then A (mod n) ⋅ B (mod n) ≡ C (mod n)
• If A ≡ B (mod n), then kA ≡ kB (mod n) for any integer ‘k’
• If A ≡ B (mod n) and C ≡ D (mod n), then AC ≡ BD (mod n)

Division

We note that modular division is different from addition, subtraction, and multiplication. This means 

${\dfrac{A}{B}\left( mod \  n\right)}$ does not equal to ${\left( \dfrac{A\left( mod \  n\right) }{B\left( mod \  n\right) }\right) \left( mod \  n\right)}$

Here, we calculate ${\dfrac{A}{B}\left( mod \  n\right)}$ using the following formula:

${\dfrac{A}{B}\left( mod \  n\right)}$ = (A × (inverse of B, if it exists)) (mod n)

However, if we add the condition that k and n are coprime to each other, then the division becomes well-defined. 

Mathematically, if gcd(k, n) = 1 and kA ≡ kB (mod n), then A ≡ B (mod n), which means if k(A – B) is a multiple of ‘n’ and gcd(k, n) = 1, then ‘n’ divides (A – B) or A ≡ B (mod n)

Multiplicative Inverse

The modular inverse of ‘A’ in modulo ‘n’ exists if only if ‘A’ and ‘n’ are relatively prime. 

Thus, if gcd(A, n) = 1 and (A ⋅ B) (mod n) = 1 ⇒ (A ⋅ B) ≡ 1 (mod n), then ‘B’ is the modular inverse of ‘A.’

For example,

A = 7, n = 9, and (7 × 4) ≡ 1 (mod 9), thus, 4 is the modular inverse of 7.

Exponentiation

If A ≡ B (mod n), then A^k ≡ B^k (mod n) for any positive integer ‘k’

Let us find the value of 2²¹ (mod 5)

Since 2⁰ ≡ 1 (mod 5)

2¹ ≡ 2 (mod 5)

2² ≡ 4 (mod 5)

2³ ≡ 3 (mod 5)

2⁴ ≡ 1 (mod 5)

We observe that the result repeats after every multiple of 4. Thus, 2²¹ ≡ (2⁴)⁵ × 2¹ ≡ 1 × 2 ≡ 2 (mod 5), means 2²¹ in modulo 5 is 2.

In the above example, we do not need to find the exact value of 2²¹, which is very large. In such cases, we can find the last digit of any number raised to a big exponent.

Using a Calculator

For calculating 1258 in modulo 4 (as ‘A’ in modulo ‘n’) using a standard calculator, we follow the following steps:

Step 1: Dividing ‘A’ by ‘n’

1258 ÷ 4 = 314.5

Step 2: Subtracting the whole Part of the Resulting Quantity

314.5 – 314 = 0.5

Step 3: Multiplying the Difference by ‘n’ to Obtain the Modulus

0.5 × 4 = 2Thus, we get 1258 ≡ 2 (mod 4)