Cardinality of a Set

The cardinality of a set is the total number of elements present in the set. It can be countable or uncountable, finite or infinite. 

For example, in the set A = {1, 3, 5, 7, 9, 11, 13, 15}, the cardinality is 8

Symbols

The cardinality of the set A is denoted by n(A) or |A|

Here, in set A = {1, 3, 5, 7, 9, 11, 13, 15}, the cardinality is written as n(A) or |A| = 8

Finite Sets

Finite sets have a finite number of elements in them. Thus, the cardinality of a finite set is always a natural number. 

Numerical Set

It is a finite set consisting of numbers. For example, the given set A = {10, 20, 30, 40, 50), contains 5 number elements, and thus the cardinal number of set A = n(A) is 5

Non-Numerical Set

It is a finite set consisting of non-numerical data. For example, the given set B = {banana, apple, watermelon, mango} contains 4 elements, and thus the cardinal number of set A = n(B) is 4

Empty Set

It is a finite set with no elements.  For example, the given set C = { } is an empty set (null set) with cardinality n(A) = n(ɸ) = 0 

Infinite Sets

These are sets with an infinite number of elements. They can be countable or uncountable.

A set may have infinitely many elements, but it is considered countable if we can define a one-to-one correspondence between its elements with the set of natural numbers. The cardinality of all natural numbers is n(ℕ) or |ℕ| = ℵ₀. Here, ℵ is the first letter from the Hebrew language, known as ‘aleph null’ (ℵ₀), representing the smallest infinite number.

If a set is countable and infinite, it is called a countably infinite set.  As a countably infinite set corresponds one-to-one with the set of natural numbers (ℕ), its cardinality is also denoted by ‘ℵ₀.’ Moreover, an uncountable set has a cardinality greater than ‘ℵ₀.’ 

Countable Sets

A set X is said to be countable if it satisfies one of the following conditions:

• If ‘X’ is a finite set.
• When there is a one-to-one correspondence from the set X to the set of natural numbers ℕ, it implies n(X) = n(ℕ). It determines whether an infinite set is countable.

A few examples of such sets include a set of  ℕ (natural numbers), ℤ (integers), and ℚ (rational numbers). Thus, the cardinality of a finite and countable set is the number of elements in that set. Meanwhile, the cardinality of an infinite and countable set is the cardinality of the set of natural numbers.

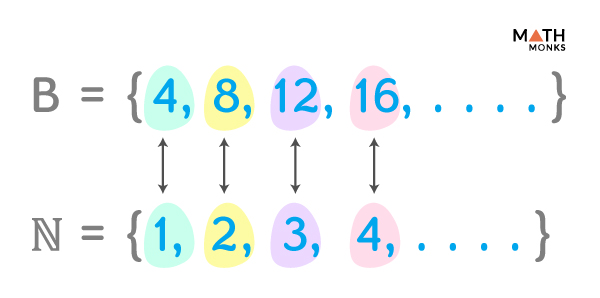
Now, let us understand the cardinality of the set B = {4, 8, 12, 16, …} with the set of natural numbers ℕ.

The above diagram shows the one-to-one correspondence of each element of set B to each element of ℕ. Here, counting the number of elements in set B is possible, even without reaching its end. 

Uncountable Sets

A set Y is considered uncountable or uncountably infinite if its elements cannot be uncounted. The set of real numbers is an example of an uncountable set. Similarly, the intervals like [a, b], (a, b], [a, b), (a, b) are also uncountable sets, where a < b. In this case, the set of natural numbers cannot be matched one-to-one with the sets. 

The uncountable infinite sets have a cardinal number of either ℵ₁ or more.

Power Sets

A power set contains all the subsets of the given set. If set A has ‘n’ number of elements, then the cardinality of its power set is 2n, which is the number of subsets of set A. 

For example, the cardinality of set A = {8, 12, 16, 20} is  |A| = 4 and the cardinality of P(A) is |P(A)| = 2⁴ = 16.

It shows that the cardinality of a power set is greater than the cardinality of the given set. 

Comparing Sets with Cardinality

If ‘A’ and ‘B’ are either two finite or infinite sets, we have:

• If there is a bijection (both one-one and onto) from the set A to the set B, then n(A) = n(B) 
• If there is an injection (one-one and may be onto) from the set A to the set B, then n(A) ≤ n(B)
• If there is an injection (one-one but strictly not onto) from the set A to the set B, then n(A) < n(B)

For example, 

Since ℕ is countable and ℝ is uncountable, n(ℕ) < n(ℝ). Thus, the cardinality of the set of natural numbers is less than that of real numbers.

Properties

Here are some rules used to determine the cardinal numbers of set(s) :

• n(A ⋃ B) = n(A) + n(B) – n(A ∩ B), where ‘A’ and ‘B’ are any two sets.
• n(A U B U C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(C ∩ A) + n(A ∩ B ∩ C), where ‘A,’ ‘B,’ and ‘C’ are any three sets.
• If ‘A’ and ‘B’ are two disjoint sets, then n(A U B) = n(A) + n(B) – n(A ∩ B)
• If two or more sets yield the same cardinal number, the relation of these sets is called an equivalence relation.

Solved Examples