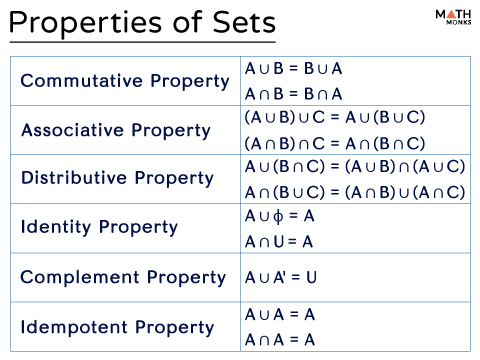
The properties of real numbers apply to sets as well. Here are the six basic properties of sets involving sets A, B, and C.
Commutative
Intersection and union of sets hold the commutative law.
- A ∪ B = B ∪ A
- A ∩ B = B ∩ A
Associative
Intersection and union of sets hold the associative law.
- (A ∪ B) ∪ C = A ∪ (B ∪ C)
- (A ∩ B) ∩ C = A ∩ (B ∩ C)
Distributive
Intersection and union of sets hold the distributive property.
- A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
- A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Identity
Complement
Idempotent
Others
Apart from the six basic properties, some more properties are used in set theory.
De Morgan’s Laws
For the Union of Sets
It states that the complement of the union of two sets is the intersection of their complements.
If A and B are two sets, then
(A ∪ B)’ = A’ ∩ B’
For the Intersection of Sets
It states that the complement of the intersection of two sets is the union of their complements.
If A and B are two sets, then
(A ∩ B)’ = A’ ∪ B’
The Principle of Duality
The properties mentioned above come in pairs of identities, where each property can be transformed into its counterpart by swapping the union (∪) with the intersection (∩) and the empty set (ɸ) with the universal set (U). This concept is known as the principle of duality.
For Two Finite Sets
If A and B are any two finite sets, then
- (A – B) ∩ B = ɸ
- B – A = B ∩ A’
- A ⊆ B ⇔ B’ ⊆ A’
- (A – B) ∪ B = A U B
- A – B = A ∩ B’
- A – B = A ⇔ A ∩ B = ɸ
- (A – B) ∪ (B – A) = (A ∪ B) – (B ∩ A)
For Three Finite Sets
If A, B, and C are any three finite sets, then
- A – (B ∩ C) = (A – B) ∪ (A – C)
- A – (B ∪ C) = (A – B) ∩ (A – C)
- A ∩ (B – C) = (A ∩ B) – (A ∩ C)
- A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Solved Examples
![]()
Find A ∪ B if A = {2, 5, 7, 12, 19} and B = {7, 12, 17, 22}, and verify that the union set follows the commutative property.
Solution:
![]()
Given A = {2, 5, 7, 12, 19} and B = {7, 12, 17, 22}
Thus, A ∪ B = {2, 5, 7, 12, 19} ∪ {7, 12, 17, 22} = {2, 5, 7, 12, 17, 19, 22}
Now, B ∪ A = {7, 12, 17, 22} ∪ {2, 5, 7, 12, 19} = {2, 5, 7, 12, 17, 19, 22}
A ∪ B = B ∪ A = {2, 5, 7, 12, 17, 19, 22}
Hence, the commutative property is verified.
![]()
Find A ∩ B if A = {2, 5, 7, 12, 19}, B = {7, 12, 17, 22}, and C = {5, 7, 35}, and verify that the intersection set follows the associative property.
Solution:
![]()
Given A = {2, 5, 7, 12, 19}, B = {7, 12, 17, 22}, and C = {5, 7, 35}
Here, A ∩ B = {2, 5, 7, 12, 19} ∩ {7, 12, 17, 22} = {7, 12}
(A ∩ B) ∩ C = {7, 12} ∩ {5, 7, 35} = {7}
Thus, the intersection of sets A, B, and C is {7}
Now, B ∩ C = {7, 12, 17, 22} ∩ {5, 7, 35} = {7}
A ∩ (B ∩ C) = {2, 5, 7, 12, 19} ∩ {7} = {7}
(A ∩ B) ∩ C = A ∩ (B ∩ C) = {7}
Hence, the associative property is verified.
![]()
Verify the distributive property A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) when A = {even prime number}, B = {8, 10, 12, 14}, and C = {x2 | 2 < x < 6 and x is a natural number}
Solution:
![]()
Given sets A = {even prime number}, B = {4, 8, 10, 12, 14}, and C = {x2 | 1 < x < 6 and x is a natural number}
⇒ A = {2}, B = {4, 8, 10, 12, 14}, and C = {4, 9, 16, 25}
Here, B ∩ C = {4, 8, 10, 12, 14} ∩ {4, 9, 16, 25} = {4}
A ∪ B = {2} ∪ {4, 8, 10, 12, 14} = {2, 4, 8, 10, 12, 14}
A ∪ C = {2} ∪ {4, 9, 16, 25} = {2, 4, 9, 16, 25}
Now, A ∪ (B ∩ C) = {2} ∪ {4} = {2, 4} and
(A ∪ B) ∩ (A ∪ C) = {2, 4, 8, 10, 12, 14} ∩ {2, 4, 9, 16, 25} = {2, 4}
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) = {2, 4}
Hence, the distributive property is verified.
![]()
If A = {3, 4, 12, 48}, find its union with an empty set.
Solution:
![]()
Given A = {3, 4, 12, 48}
Let the empty set be B = { }
Now, A ∪ B = {3, 4, 12, 48} ∪ { } = {3, 4, 12, 48} = A
Thus, the union of set A with the empty set gives the set A itself.
![]()
Verify if A = {a, e, i, o, u} and A’ = {b, c, d, f, g, h, p q, v} are complement sets when the universal set is U = {a, b, c, d, e, f, g, h, i, o, p, q, u, v}
Solution:
![]()
Given A = {a, e, i, o, u}, A’ = {b, c, d, f, g, h, p q, v}, and U = {a, b, c, d, e, f, g, h, i, o, p, q, u, v}
Using the complement property of sets, we get
A ∪ A’ = {a, e, i, o, u} ∪ {b, c, d, f, g, h, p q, v}
⇒ A ∪ A’ = {a, b, c, d, e, f, g, h, i, o, p, q, u, v}
⇒ A ∪ A’ = U, the complement property is verified.
Thus, sets A and A’ are complement sets.
