Cantor Set

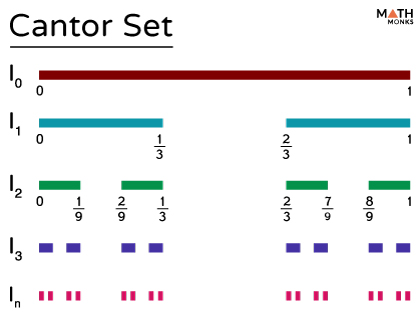
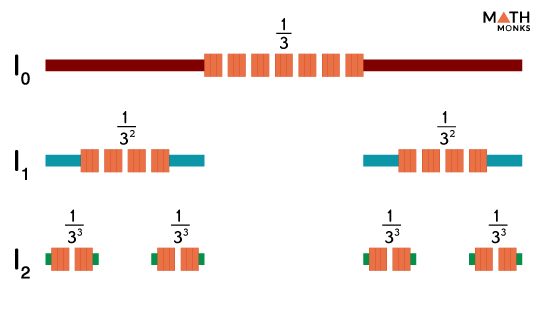
The Cantor C_∞, or the Cantor comb or no middle third set, consists of points in a line segment. It is written by taking some intervals, for example, [0, 1], and repeatedly removing the middle third of each remaining segment. It is a thus closed set consisting entirely of boundary points.

It was introduced by German mathematician Georg Cantor in 1883. 

Construction

Here are the steps to prepare a Cantor set (C) for the line segment with the interval [0, 1]: 

1. Initial Division: Dividing the interval [0, 1] into three subintervals and removing the open middle-third subinterval ${\left( \dfrac{1}{3},\dfrac{2}{3}\right)}$. 
2. Subsequent Divisions: Dividing each of the two resulting intervals into three subintervals by removing the open middle-third subintervals ${\left( \dfrac{1}{9},\dfrac{2}{9}\right)}$ and ${\left( \dfrac{7}{9},\dfrac{8}{9}\right)}$. 
3. Continuing Indefinitely: Continuing this procedure indefinitely by removing the open middle-third subintervals of each interval obtained in the previous step. 

We can obtain two copies if we magnify the cantor set from the third step.

If we continue the removal procedure indefinitely, many other points or dust will remain, which is scattered in some ways. Thus, the dust is bound together.

Now, let us describe different ways to measure the remaining dust. This will involve several mathematical applications, such as set theory, measure theory, topology, geometric measure theory, and real analysis.

Ternary Expansion of Cantor Set

The cantor set C consists of the real numbers in the interval [0, 1] whose ternary expansions (base-3) contain only the digits 0 and 2.

Examples

The golden ratio ɸ = 1.618033988… and Euler’s number e = 2.718281828… are decimal representations (base-10) of numbers.

In binary representation (base-2), these numbers can be written using two digits: 0 and 1

• The golden ratio ɸ = 1.10011110001101111…₂
• The Euler’s number e = 10.10110111111000010101…₂

Similarly, in ternary or base-3 expansions using three digits (0, 1, 2):

The fraction N (base-3) is written as N = 0.c₁c₂c₃… and is expressed  in decimal as 

N = 0.c₁c₂c₃… = c₁b^-1 + c₂b^-2 + c₃b^-3 + …

Here, 0 ≤ c_i < 3

• The golden ratio ɸ = 1.12120011…₃
• The Euler’s number e = 2.20110112…₃

The Cantor set in ternary expansion includes:

• ${\dfrac{1}{3}=0.02222\ldots}$
• ${\dfrac{2}{3}=0.20000\ldots}$
• ${\dfrac{1}{9}=0.00222\ldots}$

…

Thus, the Cantor set contains only numbers whose ternary expansion includes 0 and 2.

Formula

Mathematically, the cantor set is expressed by the formula:

C = {x ∈ [0, 1] | x = (0.c₁c₂c₃…c_n…)₃, where c_n = 0 or 2}

Properties

In Measure Theory 

The cantor set is negligible, which means its length or Lebesgue measure is 0.

Proof

The Cantor set is created by successively removing intervals. By measuring the removed intervals, we observe that at each step, the number of intervals doubles, and their length decreases by a factor of 3.

Total length of the removed intervals = ${\dfrac{1}{3}+2\cdot \dfrac{1}{3^{2}}+2^{2}\cdot \dfrac{1}{3^{3}}+\ldots =\sum ^{\infty }_{n=0}2^{n}\cdot \dfrac{1}{3^{n+1}}=\ldots =1}$, the geometric sum has its well known solution. 

The proportion remaining in the Cantor set is 1 − 1 = 0, indicating the set is negligible.

Thus, the cantor set is measurable, and its length is 0, which means the set contains no intervals of nonzero length.

In Topology

Theorem

The cantor set has no interior points.

Proof

Since the cantor set has a length of 0, it contains no intervals of nonzero length or no continuous parts.

Thus, int(C) = ɸ, and the set has no interior point.

Theorem 

The cantor set is closed.

Proof

The Cantor set is formed by removing open middle-third intervals from [0, 1]. This set complements these open intervals, which makes it closed.

Theorem 

The cantor set is nowhere dense.

Proof

The Cantor set is the intersection of closed sets and is itself closed, making it nowhere dense.

Theorem  

The cantor set is bounded.

Proof

Since the set lies within the interval [0, 1], it is bounded on the interval [0,1]. 

Moreover, a set bounded and closed in intervals is called a compact set. Thus, C is a compact set. 

Theorem

The cantor set has no isolated points.

Proof

While forming the new interval I_{n + 1} from each trisection of I_n, we obtain another point on the cantor set. Since there always exists a point from the cantor set within any neighborhood of its point, the set has no isolated points.

For example, 

If a = 0.00202…₃ ∈ C, we get another point very near to ‘a,’ say b = 0.00222…₃ ∈ C

Moreover, a compact set with no isolated points is called a perfect set. Thus, C is a perfect set.

Theorem 

The cantor set is totally disconnected.

Proof

The Cantor set can be divided into disjoint closed neighborhoods, indicating it is totally disconnected.

From the above example, we have a = 0.00202…₃ ∈ C and b = 0.00222…₃ ∈ C

It implies that if the cantor set is divided into two disjointed and closed neighborhoods of A and B, one contains ‘a’ and the other contains ‘b.’

Thus, the neighborhood of A contains all elements of C whose 4^th digit is 0, and the neighborhood of B contains all elements of C whose 4^th digit is 2.

In Set Theory

Theorem 

The cantor set is non-empty.

Proof

While forming the new interval I_{n + 1} from each trisection of I_n, we get exactly two endpoints. 

For example, 

Removing ${\left( \dfrac{1}{3},\dfrac{2}{3}\right)}$ from [0, 1] leaves the points P₀ = ${\dfrac{1}{3}}$ and P₁ = ${\dfrac{2}{3}}$

Since the cantor set C is the infinite intersection of each I_n, it contains the endpoints of each subinterval.

Thus, it is non-empty and infinite.

Theorem 

The cantor set is uncountable.

Proof

Since the cantor set contains all endpoints of the removed intervals, it is infinite and consists of more than countably many such points. 

Thus, it is uncountable.

Theorem 

The Cantor set has the same cardinality as the interval [0, 1]

Proof:

Let us define a function f: C → [0, 1] such that f(0.c₁c₂…c_n…) = ${0\cdot \dfrac{c_{1}}{2}\dfrac{c_{2}}{2}\ldots \dfrac{c_{n}}{2}\ldots}$, in binary representation. 

Here, the function f is onto. Thus, the cardinality of C is greater than or equal to (≥) the cardinality of the closed interval [0, 1] …..(i)

Also, since the cantor set C is smaller than the interval [0, 1], the cardinality of C is less than or equal to (≤) the cardinality of [0, 1] …..(ii)

Now, from (i) and (ii), the cardinality of C equals to (=) the cardinality of [0, 1]

Thus, a bijective function exists between the Cantor set and [0,1], indicating they have the same cardinality.