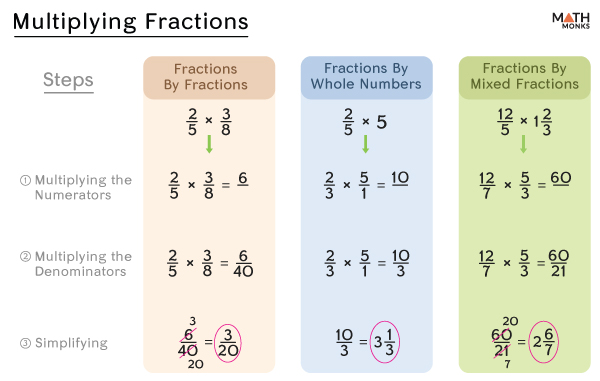
To multiply any type of fraction, we follow the following three steps:
- Multiplying the given numerators
- Multiplying the given denominators (we often perform step 1 and step 2 together)
- Simplifying or reducing the product to its lowest terms if needed.
Let us multiply ${\dfrac{2}{5}}$ and ${\dfrac{3}{8}}$
${\dfrac{2}{5}\times \dfrac{3}{8}}$
Multiplying the Numerators
2 × 3 = 6
Multiplying the Denominators
5 × 8 = 40
Now, the product is ${\dfrac{2\times 3}{5\times 8}}$
= ${\dfrac{6}{40}}$
Simplifying
The GCF of 6 and 40 is 2
Now, by dividing the numerator and the denominator by 2, we get
${\dfrac{6\div 2}{40\div 2}}$
= ${\dfrac{3}{20}}$
Here, the fractions with different denominators are multiplied. However, we can also multiply fractions with the same denominators.
Problem: Multiplying fractions with the SAME DENOMINATOR
![]() Multiply: ${\dfrac{2}{5}\times \dfrac{3}{5}}$
Multiply: ${\dfrac{2}{5}\times \dfrac{3}{5}}$
Solution:
![]()
Given, ${\dfrac{2}{5}\times \dfrac{3}{5}}$
On multiplying the numerators and the denominators,
= ${\dfrac{2\times 3}{5\times 5}}$
= ${\dfrac{6}{25}}$, which can not be simplified or reduced further.
Problem: Multiplying THREE FRACTIONS
![]() Multiply: ${\dfrac{3}{5}\times \dfrac{15}{7}\times \dfrac{14}{25}}$
Multiply: ${\dfrac{3}{5}\times \dfrac{15}{7}\times \dfrac{14}{25}}$
Solution:
![]()
Given, ${\dfrac{3}{5}\times \dfrac{15}{7}\times \dfrac{14}{25}}$
On multiplying the numerators and the denominators,
= ${\dfrac{3\times 15\times 14}{5\times 7\times 25}}$
= ${\dfrac{630}{875}}$
Simplifying the product, we get
= ${\dfrac{18}{25}}$
Thus, the product is ${\dfrac{6}{25}}$
Sometimes, we simplify the fractions first and then follow the same multiplication rules to obtain the final product more easily.
If ${\dfrac{12}{15}\times \dfrac{3}{5}}$
Simplifying the fractions, we get
${\dfrac{4}{5}\times \dfrac{3}{5}}$
On multiplying the numerators and the denominators, we get
${\dfrac{4\times 3}{5\times 5}}$
= ${\dfrac{12}{25}}$, which can not be simplified or reduced further.
Thus, the product is ${\dfrac{12}{25}}$
With Improper Fractions
Now, when multiplying ${\dfrac{2}{5}}$ by an improper fraction ${\dfrac{12}{4}}$, we follow the same steps as discussed above.
![]() Multiply the given fractions: ${\dfrac{2}{5}}$ and ${\dfrac{12}{4}}$
Multiply the given fractions: ${\dfrac{2}{5}}$ and ${\dfrac{12}{4}}$
Solution:
![]()
Given, ${\dfrac{2}{5}\times \dfrac{12}{4}}$
By multiplying the numerators and the denominators, we get
${\dfrac{2\times 12}{5\times 4}}$
= ${\dfrac{24}{20}}$
Simplifying the product, we get
= ${\dfrac{6}{5}}$
![]() Find the product: ${\dfrac{20}{7}}$ and ${\dfrac{4}{5}}$
Find the product: ${\dfrac{20}{7}}$ and ${\dfrac{4}{5}}$
Solution:
![]()
Given, the two fractions are ${\dfrac{20}{7}\times \dfrac{4}{5}}$
Multiplying the Numerators and the denominators, we get
= ${\dfrac{20\times 4}{7\times 5}}$
= ${\dfrac{80}{35}}$
Simplifying the product, we get
= ${\dfrac{16}{7}}$
The result is that of a simplified fraction and thus is the product.
With Whole Numbers
To multiply a fraction by a whole number, we multiply the numerator with the given whole number, keeping the denominator the same.
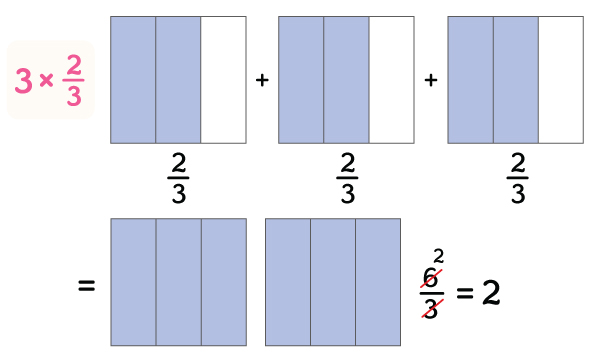
Let us multiply the fraction ${\dfrac{2}{3}}$ by a whole number ${5}$
By multiplying the numerator and the whole number,
${\dfrac{2\times 5}{3}}$
= ${\dfrac{10}{3}}$, which is in the simplest form.
Thus, the product is ${\dfrac{10}{3}}$
Now, representing this example with the visual method,
![]() Multiply ${\dfrac{2}{21}}$ by the whole number ${7}$
Multiply ${\dfrac{2}{21}}$ by the whole number ${7}$
Solution:
![]()
Given, ${\dfrac{2}{21}\times 7}$
By multiplying the numerators and the denominators, we get
= ${\dfrac{2\times 7}{21}}$
= ${\dfrac{14}{21}}$
Simplifying the product, we get
= ${\dfrac{2}{3}}$
Thus, the product is ${\dfrac{2}{3}}$
With Mixed Numbers
To multiply a fraction with a mixed number, we first convert the mixed number into an improper fraction and then follow the same steps.
If ${\dfrac{12}{7}\times 1\dfrac{2}{3}}$
Converting ${1\dfrac{2}{3}}$ into an improper fraction,
${1\dfrac{2}{3}}$ = ${\dfrac{\left( 1\times 3\right) +2}{3}}$ = ${\dfrac{5}{3}}$
Now, we have ${\dfrac{12}{7}\times \dfrac{5}{3}}$
On multiplying the numerators and the denominators,
${\dfrac{12\times 5}{7\times 3}}$
= ${\dfrac{60}{21}}$
Simplifying,
${\dfrac{20}{7}}$
Thus, the product is ${\dfrac{20}{7}}$
![]() Multiply: ${\dfrac{7}{8}\times 1\dfrac{1}{2}\times 2\dfrac{3}{4}}$
Multiply: ${\dfrac{7}{8}\times 1\dfrac{1}{2}\times 2\dfrac{3}{4}}$
Solution:
![]()
Given, ${\dfrac{7}{8}\times 1\dfrac{1}{2}\times 2\dfrac{3}{4}}$
Converting the mixed numbers into improper fractions, we get
= ${\dfrac{7}{8}\times \dfrac{3}{2}\times \dfrac{11}{4}}$
By multiplying the numerators and the denominators, we get
= ${\dfrac{7\times 3\times 11}{8\times 2\times 4}}$
= ${\dfrac{231}{64}}$, which is in the simplest form.
Thus, the product is ${\dfrac{231}{64}}$
Here is a summary of what we learned.