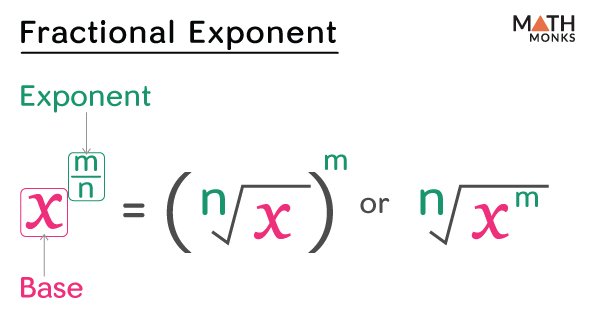Fractional Exponents

A fractional, or rational, exponent is an exponent written as a fraction. In this fraction, the numerator specifies the power to which the base is raised, while the denominator indicates the root that is applied to the base.

For example, the expression ${x^{\dfrac{m}{n}}}$ can be interpreted as taking the n^th root of x and then raising the result to the m^th power. On the other hand, it also can be interpreted as raising x to the m^th power and then taking the n^th root of the result.

Mathematically, in the general form, it is expressed as:

${x^{\dfrac{m}{n}}}$

= ${\left( \sqrt[n]{x}\right) ^{m}}$ or ${\sqrt[n]{x^{m}}}$

Here, 

• x = base
• ${\dfrac{m}{n}}$ is the fractional exponent

${5^{\dfrac{1}{2}}}$, ${7^{\dfrac{2}{3}}}$, ${3^{\dfrac{1}{4}}}$, and ${2^{\dfrac{2}{5}}}$ are a few examples of fractional exponents.

Rules

Fractional exponents follow the same rules as whole-number exponents but with an additional consideration for the root:

${x^{\dfrac{1}{n}}}$ = ${\sqrt[n]{x}}$

${x^{\dfrac{1}{m}}\times x^{\dfrac{1}{n}}}$ = ${x^{\left( \dfrac{1}{m}+\dfrac{1}{n}\right) }}$

${x^{\dfrac{1}{m}}\div x^{\dfrac{1}{n}}}$ = ${x^{\left( \dfrac{1}{m}-\dfrac{1}{n}\right) }}$

${x^{\dfrac{1}{m}}\times y^{\dfrac{1}{n}}}$ = ${\left( xy\right) ^{\dfrac{1}{n}}}$

${x^{\dfrac{1}{n}}\div y^{\dfrac{1}{n}}}$ = ${\left( x\div y\right) ^{\dfrac{1}{n}}}$

${x^{-\dfrac{m}{n}}}$ = ${\left( \dfrac{1}{x}\right) ^{\dfrac{m}{n}}}$

${\left( x^{\dfrac{m}{n}}\right) ^{\dfrac{p}{q}}}$ = ${x^{\left( \dfrac{m}{n}\times \dfrac{p}{q}\right) }}$

${x^{\dfrac{0}{n}}}$ = ${1}$

How to Solve

Let us now simplify some rational exponents using the above rules. 

For simplifying ${\left( \dfrac{27}{64}\right) ^{\dfrac{1}{3}}}$ …..(i)

Since ${\left( x\div y\right) ^{\dfrac{1}{n}}}$ = ${x^{\dfrac{1}{n}}\div y^{\dfrac{1}{n}}}$

Let x = 27 and y = 64

Now, ${x^{\dfrac{1}{n}}}$ = ${${27^{\dfrac{1}{3}}}$ = ${\sqrt[3]{27}}$ = 3

${y^{\dfrac{1}{n}}}$ = ${${64^{\dfrac{1}{3}}}$ = ${\sqrt[3]{64}}$ = 4

Substituting these values in (i), we get

${\left( \dfrac{27}{64}\right) ^{\dfrac{1}{3}}}$

= ${27^{\dfrac{1}{3}}\div 64^{\dfrac{1}{3}}}$

= ${3\div 4}$

= ${\dfrac{3}{4}}$

Thus, the fractional exponent ${\left( \dfrac{27}{64}\right) ^{\dfrac{1}{3}}}$ is simplified to ${\dfrac{3}{4}}$

Operations 

Multiplying

Let us multiply ${3^{\dfrac{2}{3}}}$ and ${5^{\dfrac{2}{3}}}$

Since ${x^{\dfrac{1}{n}}\times y^{\dfrac{1}{n}}}$ = ${\left( xy\right) ^{\dfrac{1}{n}}}$

Now, ${3^{\dfrac{2}{3}}\times 5^{\dfrac{2}{3}}}$

= ${\left( 3\times 5\right) ^{\dfrac{2}{3}}}$

= ${15^{\dfrac{2}{3}}}$

Thus, the product is ${15^{\dfrac{2}{3}}}$

Dividing

If we divide ${y^{\dfrac{2}{3}}}$ by ${y^{\dfrac{1}{7}}}$

Since ${x^{\dfrac{1}{m}}\div x^{\dfrac{1}{n}}}$ = ${x^{\left( \dfrac{1}{m}-\dfrac{1}{n}\right) }}$

Now, ${y^{\dfrac{2}{3}}\div y^{\dfrac{1}{7}}}$

= ${y^{\left( \dfrac{2}{3}-\dfrac{1}{7}\right) }}$

= ${y^{\left( \dfrac{14-3}{21}\right) }}$

= ${y^{\dfrac{11}{21}}}$

Thus, the quotient is ${y^{\dfrac{11}{21}}}$

Negative Fractional Exponents

Let us consider a fractional exponent ${81^{-\dfrac{1}{2}}}$ where the exponent ${-\dfrac{1}{2}}$ is negative.

Since ${x^{-\dfrac{m}{n}}}$ = ${\left( \dfrac{1}{x}\right) ^{\dfrac{m}{n}}}$

Now, ${81^{-\dfrac{1}{2}}}$ 

= ${\left( \dfrac{1}{81}\right) ^{\dfrac{1}{2}}}$

= ${\left( \dfrac{1}{9^{2}}\right) ^{\dfrac{1}{2}}}$

Since ${2}$ and ${\dfrac{1}{2}}$ cancel each other, the reduced form is ${\dfrac{1}{9}}$

Radical Exponents and Fractional Exponents

Radical and fractional exponents are alternate ways of expressing the same expression. Here is the table showing equivalent ways to express both.

Radical Exponents	Fractional Exponents
${\sqrt{65}}$	${65^{\dfrac{1}{2}}}$
${\sqrt[7]{83}}$	${83^{\dfrac{1}{7}}}$
${\sqrt[3]{343}}$	${343^{\dfrac{1}{3}}}$
${\sqrt[5]{32}}$	${32^{\dfrac{1}{5}}}$