A continued fraction is a mathematical form of representing real numbers as a sequence of integer divisions. Unlike regular fractions, which have a single numerator and denominator, a continued fraction is expressed as the sum of an integer and a fraction, where the fraction’s denominator itself contains another sum of an integer and a fraction, continuing this process indefinitely or until it terminates.
It provides a unique and precise way to represent numbers. It is used to approximate irrational numbers (π and √2) and has applications in control systems, digital filters, and orbital mechanics. They are also found in number theory for solving Diophantine equations and cryptography for RSA attacks.
Examples
Here are a few examples of continued fraction expansions:
Notation
Mathematically, the generalized form of a continued fraction is given by the formula:
${\dfrac{p}{q}=a_{0}+\dfrac{b_{0}}{a_{1}+\dfrac{b_{1}}{a_{2}+\dfrac{b_{2}}{a_{3}+\ldots }}}}$
Here, a0, a1, a2, … and b0, b1, b2, … are all integers.
Converting a Fraction to a Continued Fraction
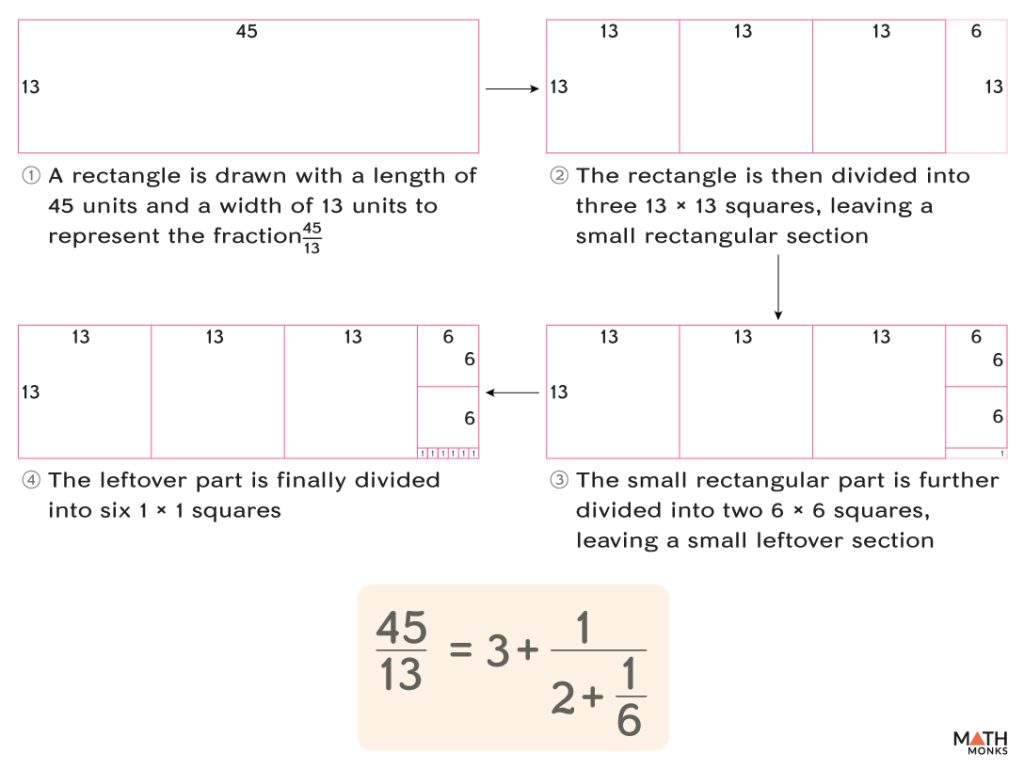
Using a rectangle
This is a visual method of getting continued fractions. Let us convert a fraction ${\dfrac{45}{13}}$ into a continued fraction by this method.
Here, we use a rectangle measuring 45 units by 13 units to represent the fraction.
To convert ${\dfrac{45}{13}}$ to a continued fraction, we express it as a whole number added to a proper fraction.
Since 45 is larger than 13, ${\dfrac{45}{13}}$ is written as
${\dfrac{45}{13}}$ = ${3+\dfrac{6}{13}}$
Here, 45 is 3 squares of sides 13 units, and a rectangle measuring 6 units by 13 units is left over. Visually, we have cut off three 13 × 13 squares from the 45 × 13 rectangle, leaving a 6 × 13 rectangle.
Next, we will rotate the 6 × 13 rectangle to view it as 13 × 6, which is expressed as
${\dfrac{6}{13}}$ = ${2+\dfrac{1}{6}}$
Now, if we rotate 1 × 6 to view it as 6 × 1,
${\dfrac{6}{1}}$ = ${6+\dfrac{0}{1}}$
Here, we have six 1 × 1 squares, and nothing is left over. Thus, the continued fraction for ${\dfrac{45}{13}}$ is
${\dfrac{45}{13}=3+\dfrac{1}{2+\dfrac{1}{6}}}$
Using Euclid’s Algorithm
This provides an algorithmic method for finding continued fractions. Let us revisit our previous calculations for ${\dfrac{45}{13}}$:
45 = 3 × 13 + 6 (45 is 3 times 13 with 6 leftover)
13 = 2 × 6 + 1 (13 is 2 times 6 with 1 leftover)
6 = 6 × 1 + 0 (6 is 6times 1 with no leftover)
The numbers 3, 2, and 6 are the terms of the continued fraction. This method is precise and works for any two numbers, always terminating as each step reduces the number of terms.
For example, let us simplify the fraction ${\dfrac{75}{45}}$ and determine its continued fraction form.
The divisors of 75 and 45 are:
75 → 1, 3, 5, 15, 25, 75
45 → 1, 3, 5, 9, 15, 45
Here, the greatest common divisor is 15
gcd(45, 75) = 15
Thus, ${\dfrac{75\div 15}{45\div 15}}$ = ${\dfrac{5}{3}}$
Now, using Euclid’s algorithm,
75 = 1 × 45 + 30
45 = 1 × 30 + 15
30 = 2 × 15 + 0
Thus, the continued fraction for ${\dfrac{75}{45}}$ is
${\dfrac{75}{45}}$ = ${1+\dfrac{1}{1+\dfrac{1}{2}}}$
Simplifying this continued fraction,
${\dfrac{75}{45}}$ = ${1+\dfrac{1}{1+\dfrac{1}{2}}}$ = ${\dfrac{5}{3}}$
Converting a Decimal to a Continued Fraction
If a number is in the decimal form, such as 1.625, we can represent them in the form of continued fractions.
1.625 = ${\dfrac{1625}{1000}}$
Now, using Euclid’s algorithm,
1625 = 1 × 1000 + 625
1000 = 1 × 625 + 375
625 = 1 × 375 + 250
375 = 1 × 250 + 125
250 = 2 × 125 + 0
Thus, the continued fraction expansion of 1.625 is
1.625 = ${1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{2}}}}}$
Types
Here are the different types of continued fractions.
Finite Continued Fractions
A finite continued fraction is a continued fraction that terminates after a finite number of steps. It represents any rational number of the form:
${\dfrac{p}{q}=a_{0}+\dfrac{b_{0}}{a_{1}+\dfrac{b_{1}}{a_{2}+\dfrac{b_{2}}{a_{3}+\ldots +\dfrac{1}{a_{n}}}}}}$
For example,
${\dfrac{75}{45}}$ = ${1+\dfrac{1}{1+\dfrac{1}{2}}}$, which is also written in the list notation as [1; 1, 2]
If the first number in the list is 0, then the fraction represented is less than 1.
For example,
${\dfrac{7}{25}}$ = ${0+\dfrac{1}{3+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{3}}}}}$
Infinite Continued Fractions
An infinite continued fraction represents an irrational number and does not terminate.
Here are a few examples of irrational numbers in infinite continued fraction expansions:
- π (pi) = ${3+\dfrac{1}{7+\dfrac{1}{15+\dfrac{1}{1+\dfrac{1}{292+\ldots }}}}}$ = [3; 7, 15, 1, 292, …]
- e (Euler’s number) = ${2+\dfrac{1}{1+\dfrac{1}{2+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{4+\ldots }}}}}}$ = [2; 1, 2, 1, 1, …]
- ɸ (phi, golden ratio) = ${1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\ldots }}}}}$ = [1; 1, 1, 1, 1, …]
- ${\sqrt{2}}$ = ${1+\dfrac{1}{2+\dfrac{1}{2+\dfrac{1}{2+\dfrac{1}{2+\ldots }}}}}$ = [1; 2, 2, 2, 2, …]
Simple Continued Fraction
When all the bi are equal to 1, the continued fraction is called a simple continued fraction.
Mathematically, it is expressed as
${\dfrac{p}{q}=a_{0}+\dfrac{1}{a_{1}+\dfrac{1}{a_{2}+\dfrac{1}{a_{3}+\ldots }}}}$. This is just a list of numbers a0, a1, a2, a3, …, and a0 is the whole number part of the value.
Moreover, ${\dfrac{p}{q}}$ can be written in a more compact form as:
a0 (the first number), then a semicolon (;), and finally, the rest as a list with comma separators (,) like this:
${\dfrac{p}{q}}$ = [a0; a1, a2, a3, …], which is known as the list notation.
These representations can be finite or infinite, depending on whether the number is rational or irrational.
Periodic Continued Fraction
When all the ai and bi are equal to 1, the continued fraction is called a periodic continued fraction.
Mathematically, it is expressed as
${\dfrac{p}{q}=1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\ldots }}}}$
= [1; 1, 1, 1, …], in the list notation.
Convergence
Convergence of continued fraction refers to how the sequence of fractions generated by a continued fraction approaches the actual value of the number being represented.
If more terms of continued fractions are included, the resulting fractions (known as convergent) yield a better approximation of the original number.
To find the best rational approximations of a real number, we check the fractions with increasingly larger denominators and identify which ones are closer to the target value than any previous fractions with smaller denominators.
For example,
Here is a list of fractions for π = 3.141592653589793… in which each fraction is the best approximation using the smallest possible denominator:
${\dfrac{3}{1}}$, ${\dfrac{22}{7}}$, ${\dfrac{333}{106}}$, ${\dfrac{355}{113}}$
These fractions include all the convergents in the continued fraction expansion of π.
Now, finding a few approximations,
- ${\dfrac{3}{1}}$ = 3, the nearest whole number
- ${3+\dfrac{1}{7}}$ = ${\dfrac{22}{7}}$ = 3.142857, error of +0.001264
- ${3+\dfrac{1}{7+\dfrac{1}{15}}}$ = ${\dfrac{333}{106}}$ = 3.141509, error of -0.000083
- ${3+\dfrac{1}{7+\dfrac{1}{15+\dfrac{1}{1}}}}$ = ${\dfrac{355}{113}}$ = 3.1415929, error of +0.0000003
These fractions alternate between being slightly above and slightly below π, showing the precision of continued fractions in approximating real numbers. Also, we observe that convergents tend to converge to the original number.
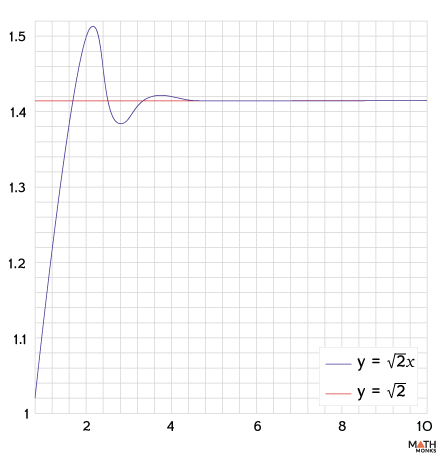
Graphical Representation
Graphically, each convergent ${\dfrac{p}{q}}$ can be represented as a point (x,y) on a graph. For an irrational value r, each convergent gets closer to the line y = rx.
For example,
${\sqrt{2}}$ (= 1.41421356…)
Now, if a string is tied from the origin along the line y = √2x, it will touch the grid points corresponding to the convergents, as shown.
The above graph shows how convergents alternate between above and below the true value, giving the best possible rational approximations.