An area model uses a rectangle to demonstrate the multiplication of two fractions visually.
The rectangle is divided into parts according to the denominators of the fractions: one fraction is represented along the length and the other along the width. The overlapping sections within the rectangle then reveal the product of the fractions, making it easier to understand the concept visually.
Here is a video showing the multiplication of two fractions.
Steps
Let us multiply ${\dfrac{2}{5}\times \dfrac{3}{4}}$
Drawing a Rectangle
First, we will draw a large rectangle.
Representing the First Fraction
The denominator of the first fraction indicates the number of columns to divide the rectangle into, while the numerator tells us how many of those columns should be shaded.
Here, ${\dfrac{2}{5}}$ represents 2 shaded columns out of 5 columns of the rectangle.
Representing the Second Fraction
The denominator of the second fraction determines the number of rows to divide the rectangle into, while the numerator specifies how many of those rows should be shaded.
Here, ${\dfrac{3}{4}}$ represents 3 shaded rows out of 4 rows in the rectangle.
Finding the Product
The numerator of the product is the number of sections that have been shaded twice (the overlapping area), while the denominator is the total number of sections within the rectangle.
Here, 6 parts are shaded twice out of 20 total parts.
Thus, the product is ${\dfrac{6}{20}}$
Simplifying (If Necessary)
Simplifying further, we get
${\dfrac{6}{20}}$ = ${\dfrac{3}{10}}$
![]() Multiply the following fractions using the area model:
Multiply the following fractions using the area model:
${\dfrac{1}{2}\times \dfrac{2}{3}}$
Solution:
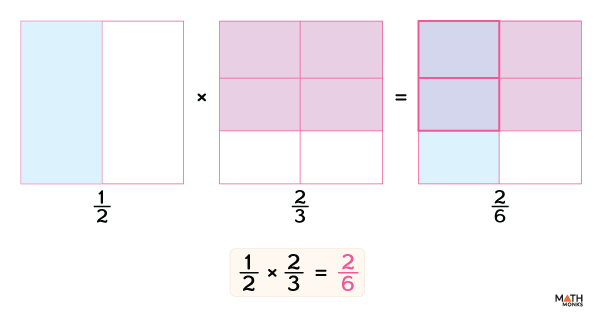
Given, ${\dfrac{1}{2}\times \dfrac{2}{3}}$
= ${\dfrac{2}{6}}$
Simplifying further, we get
${\dfrac{1}{3}}$
Thus, the product is ${\dfrac{1}{3}}$
 What two fractions are being multiplied in this given model?
What two fractions are being multiplied in this given model?
Solution:
![]()
Here, the given area model represents ${\dfrac{1}{6}\times \dfrac{3}{5}}$
Problem – Multiplying Fractions and WHOLE NUMBERS
![]() Multiply ${\dfrac{2}{5}}$ by ${3}$
Multiply ${\dfrac{2}{5}}$ by ${3}$
Solution:
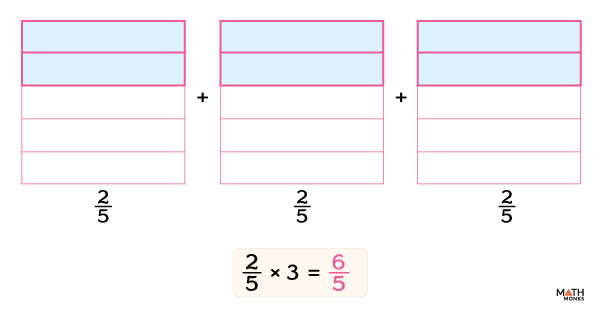
Given, ${\dfrac{2}{5}\times 3}$
Thus, the product is ${\dfrac{6}{5}}$
Problem – Multiplying Fractions and MIXED NUMBERS
![]() Multiply ${\dfrac{2}{5}}$ by ${1\dfrac{1}{4}}$
Multiply ${\dfrac{2}{5}}$ by ${1\dfrac{1}{4}}$
Solution:
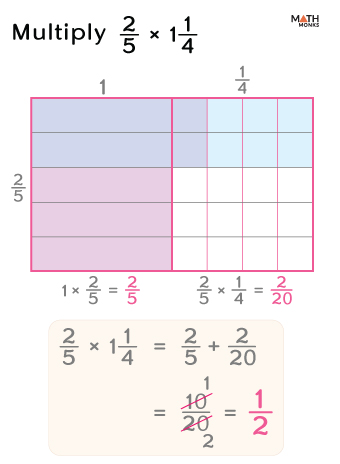
Given, ${\dfrac{2}{5}}$ by ${1\dfrac{1}{4}}$
Thus, the product is ${\dfrac{1}{2}}$





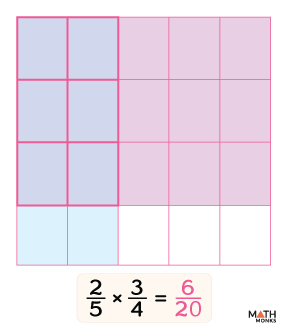

 What two fractions are being multiplied in this given model?
What two fractions are being multiplied in this given model?
