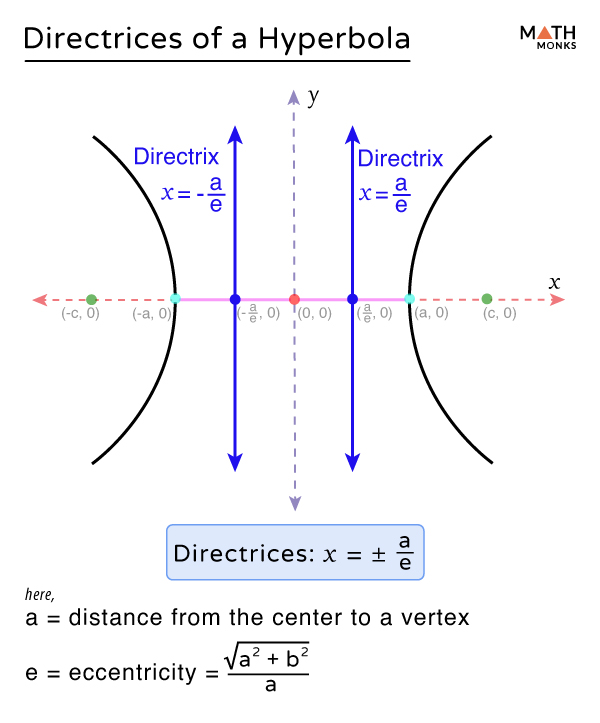
The directrix of a hyperbola is a straight line perpendicular to its transverse axis that is used to describe the relationship between any point on the hyperbola and its corresponding focus. This relationship is explained by the distance of the point from the focus and the directrix.
For any point on the hyperbola, the ratio of the distance to the focus and the distance to the directrix is always constant.
Formula
For any hyperbola centered at the origin ${\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1}$ and ${sqrt{a^{2}+b^{2}=c^{2}}$ with the transverse axis along the x-axis, the directrices are vertical lines given by the equation
${x=\pm \dfrac{a}{e}}$ or ${\pm \dfrac{a^{2}}{c}}$
Here,
- a = distance from the center to a vertex along the transverse axis (the length of the semi-major axis)
- c (focal length) = distance from the center to any focus
- Eccentricity ${e=\dfrac{\sqrt{a^{2}+b^{2}}}{a}}$
Thus, the directrix lies on the same plane as the hyperbola. The distance of the directrix from the center affects the hyperbola’s shape: a closer directrix leads to tighter branches, while a more distant directrix results in a wider, more open curve.
How To Find
Here are two different ways to find the directrix of hyperbola, as shown.
Using Focus Length
Let us find the directrix of the hyperbola given by the equation ${\dfrac{x^{2}}{16}-\dfrac{y^{2}}{9}=1}$
Here, we will first find the focus length c and then use the above formula to calculate the directrix.
Comparing the given equation ${\dfrac{x^{2}}{16}-\dfrac{y^{2}}{9}=1}$ …..(i) with the standard equation of the hyperbola ${\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1}$ …..(ii), we get
a = 4 and b = 3
Now, ${c=\sqrt{a^{2}+b^{2}}}$
⇒ ${c=\sqrt{4^{2}+3^{2}}}$
⇒ ${c=\sqrt{16+9}}$
⇒ ${c=\sqrt{25}}$
⇒ ${c=5}$
As we know, the formula to find the directrix of the hyperbola is: ${x=\pm \dfrac{a^{2}}{c}}$
⇒ ${x=\pm \dfrac{4^{2}}{5}}$
⇒ ${x=\pm \dfrac{16}{5}}$
Using Eccentricity
We can also find the directrix of a hyperbola using its eccentricity.
If we are given to find the directrix for the hyperbola ${\dfrac{x^{2}}{16}-\dfrac{y^{2}}{9}=1}$, we will find its eccentricity and then use the above formula to calculate the directrix.
On comparing the given equation ${\dfrac{x^{2}}{16}-\dfrac{y^{2}}{9}=1}$ …..(i) with the standard equation of the hyperbola, ${\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1}$ …..(ii), we get
a = 4 and b = 3
Now, ${e=\dfrac{\sqrt{a^{2}+b^{2}}}{a}}$
⇒ ${e=\dfrac{\sqrt{4^{2}+3^{2}}}{4}}$
⇒ ${e=\dfrac{5}{4}}$
As we know, the formula to find the directrix of the hyperbola is: ${x=\pm \dfrac{a}{e}}$
${x=\pm \dfrac{a}{e}}$
⇒ ${x=\pm \dfrac{4}{\dfrac{5}{4}}}$
⇒ ${x=\pm 4\times \dfrac{4}{5}}$
⇒ ${x=\pm \dfrac{16}{5}}$
Thus, ${x=\pm \dfrac{16}{5}}$ is the directrix of the hyperbola ${\dfrac{x^{2}}{16}-\dfrac{y^{2}}{9}=1}$
![]() Find the directrix of the hyperbola ${\dfrac{x^{2}}{36}-\dfrac{y^{2}}{64}=1}$
Find the directrix of the hyperbola ${\dfrac{x^{2}}{36}-\dfrac{y^{2}}{64}=1}$
Solution:
![]()
Given, ${\dfrac{x^{2}}{36}-\dfrac{y^{2}}{64}=1}$
The standard equation of the hyperbola is ${\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1}$
On comparing both equations, we get
a = 6 and b = 8
As we know, ${c=\sqrt{a^{2}+b^{2}}}$
Here, ${c=\sqrt{6^{2}+8^{2}}}$
⇒ ${c=\sqrt{36+64}}$
⇒ ${c=\sqrt{100}}$
⇒ ${c=10}$
As we know, the directrix of the hyperbola is
${x=\pm \dfrac{a^{2}}{c}}$
⇒ ${x=\pm \dfrac{6^{2}}{10}}$
⇒ ${x=\pm \dfrac{36}{10}}$
⇒ ${x=\pm \dfrac{18}{5}}$
Thus, ${x=\pm \dfrac{18}{5}}$is the directrix of the hyperbola.
Finding Distance Between the Directrices
The directrices are equidistant from the center of the hyperbola, and the distance between them is found using the hyperbola’s semi-major axis and eccentricity.
For a hyperbola centered at the origin, the distance between the directrices is given by the formula:
${\dfrac{2a}{e}}$ units.
Here,
- a = the length of the semi-major axis
- b = the length of the semi-minor axis
- Eccentricity ${e=\dfrac{\sqrt{a^{2}+b^{2}}}{a}}$
Thus, by substituting the value of e, the distance between the directrices becomes
${\dfrac{2a}{\dfrac{\sqrt{a^{2}+b^{2}}}{a}}}$ or ${\dfrac{2a}{\sqrt{1+\dfrac{b^{2}}{a^{2}}}}}$
Now, let us find the distance between the directrices of the hyperbola ${\dfrac{x^{2}}{36}-\dfrac{y^{2}}{64}=1}$
On comparing the hyperbola with its standard form ${\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1}$, we get
a = 6 snd b = 8
Here, ${e=\dfrac{\sqrt{a^{2}+b^{2}}}{a}}$
⇒ ${e=\dfrac{\sqrt{6^{2}+8^{2}}}{6}}$
⇒ ${e=\dfrac{10}{6}}$
⇒ ${e=\dfrac{5}{3}}$
Now, the distance between the directrices of the hyperbola is ${\dfrac{2a}{e}}$
= ${\dfrac{2\times 6}{\dfrac{5}{3}}}$
= ${\dfrac{12}{\dfrac{5}{3}}}$
= ${12\times \dfrac{3}{5}}$
= ${\dfrac{36}{5}}$
Thus, the distance between the directrices of the hyperbola is ${\dfrac{36}{5}}$ units.
![]() If the hyperbola is given by the equation ${\dfrac{x^{2}}{16}-\dfrac{y^{2}}{9}=1}$, find the distance between its directrices.
If the hyperbola is given by the equation ${\dfrac{x^{2}}{16}-\dfrac{y^{2}}{9}=1}$, find the distance between its directrices.
Solution:
![]()
The distance between the directrices of the hyperbola is ${\dfrac{2a}{e}}$
Given, ${\dfrac{x^{2}}{16}-\dfrac{y^{2}}{9}=1}$
The standard equation of the hyperbola is ${\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1}$
On comparing both equations, we get
a = 4 and b = 3
Here, ${e=\dfrac{\sqrt{a^{2}+b^{2}}}{a}}$
⇒ ${e=\dfrac{\sqrt{4^{2}+3^{2}}}{4}}$
⇒ ${e=\dfrac{5}{4}}$
Now, the distance between the directrices of the hyperbola is
${\dfrac{2a}{e}}$
= ${\dfrac{2\times 4}{\dfrac{5}{4}}}$
= ${\dfrac{8}{\dfrac{5}{4}}}$
= ${8\times \dfrac{4}{5}}$
= ${\dfrac{32}{5}}$
Thus, the distance between the directrices of the hyperbola is ${\dfrac{32}{5}}$ units.