Rectangular Hyperbola

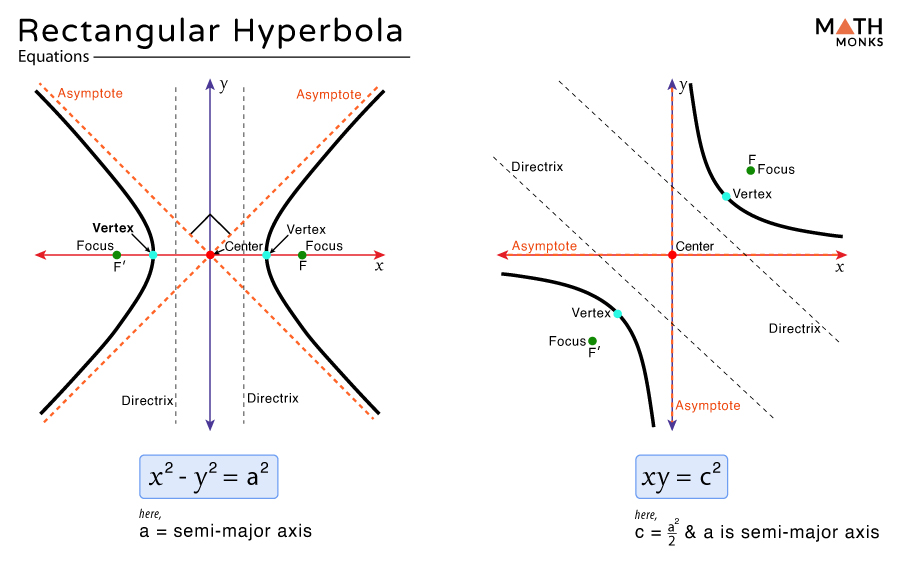
A rectangular hyperbola, also known as an equilateral hyperbola, is a special type of hyperbola in which the transverse and conjugate axes are of equal length. It shares all the properties of a general hyperbola, with the main difference being its asymptotes are perpendicular to each other (orthogonal), forming a right angle.

Given that the transverse axis has a length of 2a and the conjugate axis has a length of 2b, we have 2a = 2b, which simplifies to a = b. 

Equations

Based on its center and asymptotes, the equation of a hyperbola has two forms: standard and parametric.

Standard Form – Centered at (0, 0)

The general equation of a Rectangular Hyperbola centered at (0, 0) is:

x² – y² = a² 

If the center is at (0, 0) but the asymptotes are aligned with the horizontal and vertical axes (x and y axes), then the general equation changes to:

xy = c², here c² = ${\dfrac{a^{2}}{2}}$ is a constant that determines the scale of the hyperbola.

Standard Form – Not Centered at (0, 0)

If the center is located anywhere apart from the center, say (x₀, y₀), then the equation of the rectangular hyperbola becomes:

(x – x₀)² – (y – y₀)² = a² 

Parametric Form

The parametric equation of a rectangular hyperbola is:

x = a secθ

y = a tanθ

However, unlike general hyperbolas, rectangular hyperbolas range over all angles where the secant and tangent functions are defined. The range typically spans from 0° to 180° (i.e., 0° ≤ θ ≤ 180°) except where secθ and tanθ are undefined (i.e., where cosθ = 0 or sinθ = 0)

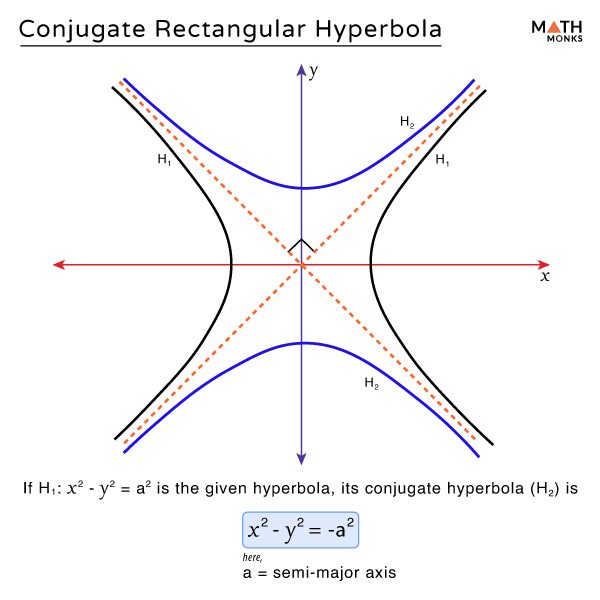
Conjugate 

The conjugate of the rectangular hyperbola x² – y² = a² is also a rectangular hyperbola. The equation of its conjugate is x² – y² = -a². The transverse and conjugate axes of a hyperbola become the conjugate and transverse axes of its conjugate. Together, these axes form a pair of asymptotes.

Asymptotes

For a rectangular hyperbola, the equation of the asymptotes is:

y = ±x or x² – y² = 0 

Thus, the asymptotes are parallel.

Eccentricity

As we know, the eccentricity of the hyperbola is ${e=\dfrac{\sqrt{a^{2}+b^{2}}}{a}}$

Since, in a rectangular hyperbola, a = b

${e=\dfrac{\sqrt{a^{2}+b^{2}}}{a}}$ 

⇒ ${e=\dfrac{\sqrt{a^{2}+a^{2}}}{a}}$

⇒ ${e=\sqrt{2}}$

Thus, the eccentricity of a rectangular hyperbola is ${\sqrt{2}}$ 

Foci

As we know, the foci of the hyperbola are (±ae, o)

Since, in a rectangular hyperbola, the eccentricity is e = ${\sqrt{2}}$

Thus, the foci of a rectangular hyperbola is ${\left( \pm a\sqrt{2},0\right)}$ 

Directrix

As we know, the directrices of the hyperbola is ${y=\pm \dfrac{a}{e}}$

Since the eccentricity of a rectangular hyperbola is e = ${\sqrt{2}}$

Thus, in a rectangular hyperbola, the equation of the directrices is ${y=\pm \dfrac{a}{\sqrt{2}}}$

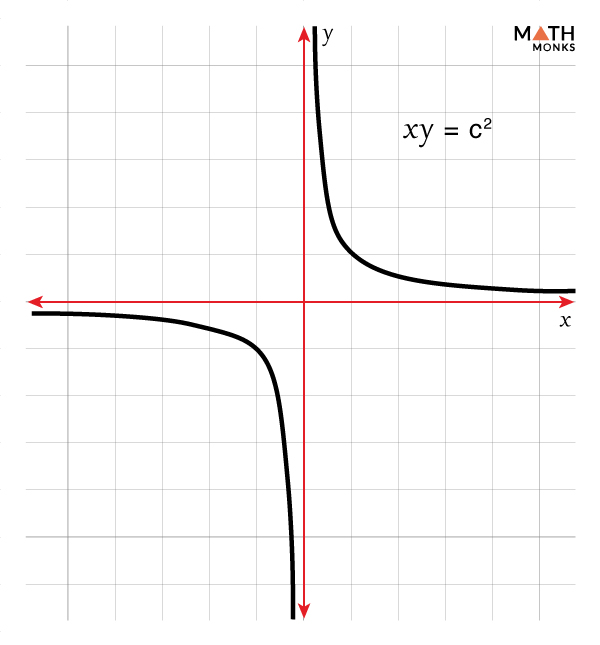
Graphing

The graph of the Rectangular Hyperbola with the equation xy = c² (c is a constant) is shown.

The graph of the equation ${y= \dfrac{1}{x}}$ is similar to the graph of a rectangular hyperbola.

Solved Examples