Last modified on November 19th, 2024

chapter outline

 

Focus and Directrix of a Parabola

A parabola is a U-shaped curve in which all points are equidistant from a fixed point and a fixed straight line. The point is the focus of the parabola, and the line is the directrix. 

The focus lies on the axis of symmetry, and the directrix is parallel to either the x-axis or the y-axis. However, the focus never lies on the directrix.

Formulas

Parabolas Centered at (0, 0)

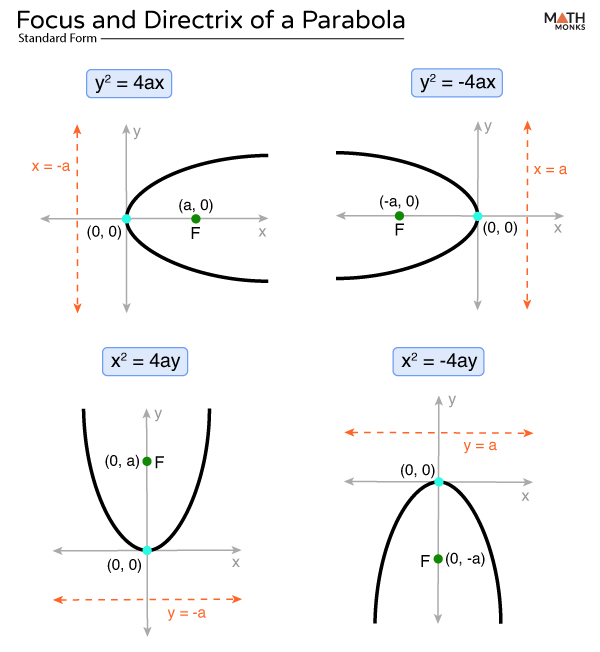
The focus and the directrix for the standard equations of a parabola centered at (0, 0) are:

For y2 = 4ax

  • Focus is at (a, 0)
  • The equation of the directrix is x + a = 0 

For y2 = -4ax

  • Focus is at (-a, 0)
  • The equation of the directrix is x – a = 0

For x2 = 4ay

  • Focus is at (0, a)
  • The equation of the directrix is y + a = 0

For x2 = -4ay

  • Focus is at (0, -a)
  • The equation of the directrix is y – a = 0
Focus and Directrix of a Parabola in Standard Form

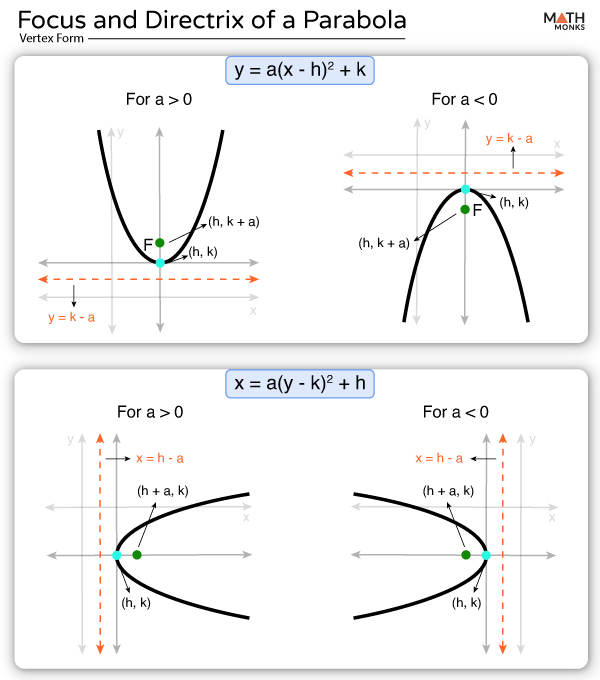
Parabolas Centered at (h, k)

For (x – h)2 = 4a(y – k)

  • Focus is at (h, k + a)
  • Directrix is y = k – a

Note: If the parabola is in vertex form y = a(x – h)2 + k, then the focus is at ${\left( h,k+\dfrac{1}{4a}\right)}$ and directrix is ${y=k-\dfrac{1}{4a}}$

For (y – k)2 = 4a(x – h)

  • Focus is at (h + a, k)
  • Directrix is x = h – a

Note: If the parabola is in the vertex form as x = a(y – k)2 + h, then the focus is at ${\left( h+\dfrac{1}{4a},k\right)}$ and directrix is ${x=h-\dfrac{1}{4a}}$

Focus and Directrix of a Parabola in Vertex Form

How To Find

Let us find the focus and the directrix of the parabola (x – 3)2 = -8(y – 5) 

Identifying the Parabola

Given, (x – 3)2 = -8(y – 5) …..(i)

The given equation is of the form: (x – h)2 = 4a(y – k) …..(ii)

Comparing the equations (i) and (ii), we get

a = -2, h = 3, and k = 5

Finding the Focus

Here, the focus is at (h, k + a) = (3, 5 – 2) = (3, 3)

Finding the Directrix

The directrix is y = k – a 

⇒ y = 5 – (-2) 

⇒ y = 7

Thus, the focus is at (3, 3), and the directrix is y = 7

Solved Examples

Find the focus and directrix of the parabola y2 = 8x

Solution:

Given, y2 = 8x …..(i)
The given equation is of the form: y2 = 4ax …..(ii)
Comparing the equations (i) and (ii), we have
a = 2
Here, the focus is at (a, 0) = (2, 0)
The equation of the directrix is x + a = 0 ⇒ x + 2 = 0 ⇒ x = -2
Thus, the focus is at (2, 0), and the directrix is x = -2

Find the vertex, focus, and directrix of the parabola given by the equation (x – 2)2 = 12(y – 3)

Solution:

Given, (x – 2)2 = 12(y – 3) …..(i)
The given equation is of the form: (x – h)2 = 4a(y – k) …..(ii)
Comparing the equations (i) and (ii), we have
a = 3, h = 2, and k = 3
Here, the vertex is at (h, k) = (2, 3)
The focus is at (h, k + a) = (2, 3 + 3) = (2, 6)
The directrix is y = k – a 
⇒ y = 3 – 3 
⇒ y = 0
Thus, the vertex is at (2, 3), the focus is at (2, 6), and the directrix is y = 0

Determine the focus and directrix of y = -(x – 2)2 – 4

Solution:

Given, y = -(x – 2)2 – 4 …..(i)
⇒ (y + 4) = -(x – 2)2
⇒ (x – 2)2 = – (y + 4) …..(ii)
The given equation is of the form: (x – h)2 = 4a(y – k) …..(iii)
Comparing the equations (ii) and (iii), we have
a = ${-\dfrac{1}{4}}$, h = 2, and k = -4
Here, the focus is at (h, k + a) = ${\left( 2,-4-\dfrac{1}{4}\right)}$ = (2, -4.25)
The directrix is y = k – a 
⇒ y = ${-4-\left( -\dfrac{1}{4}\right)}$ 
⇒ y = -3.75
Thus, the focus is at (2, -4.25), and the directrix is y = -3.75

Problem – Finding the equation of the parabola when FOCUS and DIRECTRIX are known

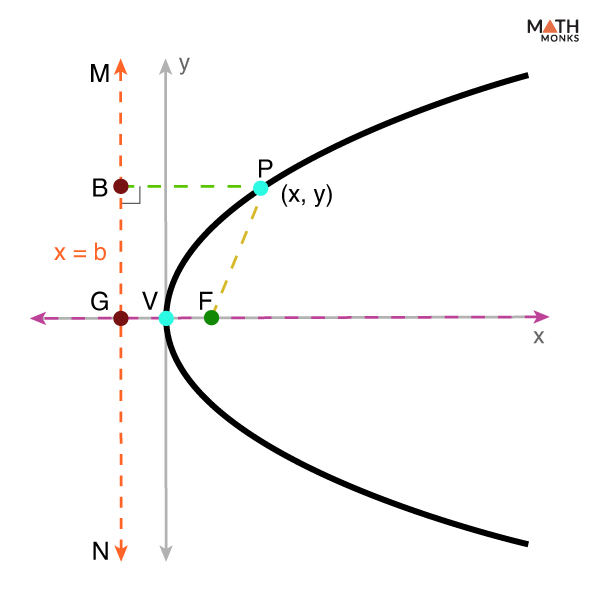
Parabola from Focus and Directrix

Let F be the focus, and the line MN represents the directrix. 

Now, a perpendicular line FG is drawn from F on the directrix and bisect it at V.

Then, VF = VG ⇒ Distance of V from the focus = Distance of V from the directrix

By the definition of the parabola, since V lies on the parabola, FG = 2a ⇒ VF = VG = a

Let us consider V as the vertex. Then, VG is perpendicular to the directrix and parallel to the x-axis. 

The coordinates of the focus F are (h, k), and the equation of the directrix MN is x = b. 

Since PB is perpendicular to the directrix x = b, and point B is with the coordinates (b, y)

Let us consider a point P(x, y) on the parabola. Now, FP and PB are joined.

As we know, P lies on the parabola.

Now, FP = PB

⇒ FP2 = PB2 

⇒ (x – h)2 + (y – k)2 = (x – b)2 + (y – y)2

⇒ x2 – 2hx + h2 + (y – k)2 = x2 – 2bx + b2 

On adding (2hx – b2) on both sides, we get

⇒ x2 – 2hx + h2 + 2hx – b2 + (y – k)2 = x2 – 2bx + b2 + 2hx – b2

⇒ 2(h – b)x = (y – k)2 + h2 – b2 

On dividing equation by 2(h – b), we get

${x=\dfrac{\left( y-k\right) ^{2}}{2\left( h-b\right) }+\dfrac{h^{2}-b^{2}}{2\left( h-b\right) }}$

⇒ ${x=\dfrac{\left( y-k\right) ^{2}}{2\left( h-b\right) }+\dfrac{\left( h+b\right) }{2}}$ …..(i)

Similarly, when directrix y = b, we get

${y=\dfrac{\left( x-h\right) ^{2}}{2\left( k-b\right) }+\dfrac{\left( k+b\right) }{2}}$ …..(ii)

When V is the origin, VF is the x-axis of length a. Then, the coordinates of F will be (a, 0), and the directrix MN is x = -a.

h = a, k = 0 and b = -a

Using the equation (i), we get

${x=\dfrac{\left( y-0\right) ^{2}}{2\left( a-\left( -a\right) \right) }+\dfrac{\left( a+\left( -a\right) \right) }{2}}$

⇒ ${x=\dfrac{y^{2}}{4a}}$

⇒ y2 = 4ax

Derive the equation of a parabola with focus (0, 2) and directrix y = −2

Solution:

The vertex is the midpoint between the focus and directrix, which is (0,0). The distance from the vertex to the focus is a = 2Using the formula y2 = 4ax, the equation of the parabola is y2 = 8x

Last modified on November 19th, 2024