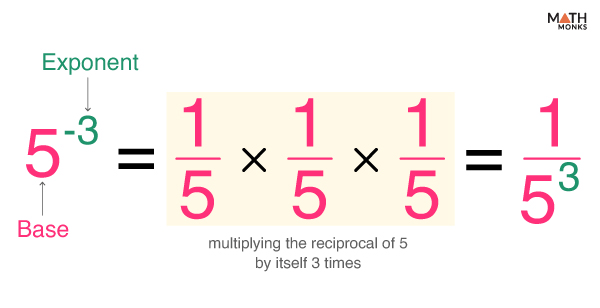A negative exponent is defined as the reciprocal (or multiplicative inverse) of the base, raised to the corresponding positive exponent.
Thus, while positive exponents involve repeated multiplication of a number, negative exponents indicate how many times to divide by that number.
Thus, 5-3 = ${\dfrac{1}{125}}$
Here are a few more examples of negative exponents:
- 8-3 = ${\dfrac{1}{8^{3}}}$ = ${\dfrac{1}{512}}$
- 7-2 = ${\dfrac{1}{7^{2}}}$ = ${\dfrac{1}{49}}$
- 3-5 = ${\dfrac{1}{3^{5}}}$ = ${\dfrac{1}{243}}$
Thus, larger negative exponents represent smaller numbers.
Rules
We follow a set of rules while simplifying problems involving negative exponents. These rules are applied along with the basic exponent rules.
Rule 1
It states that for base x with the negative exponent -n, we take the reciprocal of the base ${\dfrac{1}{x}}$ and multiply it by itself n times.
${x^{-n}=\dfrac{1}{x^{n}}}$
Rule 2
Rule 1 remains the same even when there is a negative exponent in the denominator:
${\dfrac{1}{x^{-n}}=x\times x\times \ldots \times x}$ (n times) = xn
Multiplying
When multiplying exponents, we follow the following rules:
- If the bases are the same, the exponents are added
- If the bases are different but the exponents are the same, the bases are multiplied by keeping the exponents unchanged.
For example,
2-3 × 2-2 = 2-3 + (-2) = 2-5
Dividing
When dividing exponents, we follow the following rules:
- If the bases are the same, the exponents are subtracted
- If the bases are different but the exponents are the same, the bases are divided by keeping the exponents unchanged.
For example,
${\dfrac{2^{-3}}{2^{-2}}}$ = 2-3 – (-2) = 2-1
Solved Examples
![]()
Evaluate:
a) 3-3
b) 5-1
c) 8-2
Solution:
![]()
a) Here, 3-3 = ${\dfrac{1}{3^{3}}}$ = ${\dfrac{1}{27}}$
b) Here, 5-1 = ${\dfrac{1}{5^{1}}}$ = ${\dfrac{1}{5}}$
c) Here, 8-2 = ${\dfrac{1}{8^{2}}}$ = ${\dfrac{1}{64}}$
![]()
Apply the negative exponent rule to simplify:
a) ${\dfrac{1}{5^{-2}}}$
b) ${\dfrac{1}{2^{-4}}}$
c) ${\dfrac{1}{10^{-3}}}$
Solution:
![]()
a) Here, ${\dfrac{1}{5^{-2}}}$ = 52 = 25
b) Here, ${\dfrac{1}{2^{-4}}}$ = 24 = 16
c) Here, ${\dfrac{1}{10^{-3}}}$ = 103 = 1000
![]()
Convert the following fractions into expressions with positive exponents:
a) ${\dfrac{1}{9^{5}}}$
b) ${\dfrac{1}{12^{2}}}$
c) ${\dfrac{1}{4^{7}}}$
Solution:
![]()
a) Here, ${\dfrac{1}{9^{5}}}$ = 9-5
b) Here, ${\dfrac{1}{12^{2}}}$ = 12-2
c) Here, ${\dfrac{1}{4^{7}}}$ = 4-7
![]()
Apply the exponent rules to multiply the expression with negative exponents 2-3 × 24 × 2-2
Solution:
![]()
Given, 2-3 × 24 × 2-2
Using the product rule,
= 2-3 + 4 – 2
= 2-1
Using the negative exponent rule,
= ${\dfrac{1}{2}}$
Thus, 2-3 × 24 × 2-2 = ${\dfrac{1}{2}}$
![]()
Divide the expression with negative exponents ${\dfrac{8^{-2}}{8^{-6}}}$
Solution:
![]()
Given, ${\dfrac{8^{-2}}{8^{-6}}}$
Using the quotient rule,
= 8-2 – (-6)
= 84
![]()
Simplify:
a) ${\dfrac{10^{-2}\times 5^{-3}}{10^{-5}}}$
b) ${\dfrac{4^{-3}\times 2^{-2}}{4^{-1}\times 2^{-4}}}$
Solution:
![]()
a) Given, ${\dfrac{10^{-2}\times 5^{-3}}{10^{-5}}}$
Using the quotient rule,
= ${10^{-2-\left( -5\right) }\times 5^{-3}}$
= ${10^{3}\times 5^{-3}}$
Using the power of product rule,
= ${\left( 2\times 5\right) ^{3}\times 5^{-3}}$
= ${2^{3}\times 5^{3}\times 5^{-3}}$
Using the product rule,
= 23 × 53 + (-3)
= 23 × 50
Using the zero exponent rule,
= 23 × 1
= 8
Thus, ${\dfrac{10^{-2}\times 5^{-3}}{10^{-5}}}$ = 8
b) Given, ${\dfrac{4^{-3}\times 2^{-2}}{4^{-1}\times 2^{-4}}}$
Using the power of the quotient rule,
= ${\dfrac{4^{-3}}{4^{-1}}\times \dfrac{2^{-2}}{2^{-4}}}$
Using the quotient rule,
= 4-3 – (-1) × 2-2 – (-4)
= 4-2 × 22
= (22)-2 × 22
Using the power of power rule,
= 2-4 × 22
Using the product rule,
= 2-4 + 2
= 2-2
Using the negative exponent rule,
= ${\dfrac{1}{2^{2}}}$
= ${\dfrac{1}{4}}$
Thus, ${\dfrac{4^{-3}\times 2^{-2}}{4^{-1}\times 2^{-4}}}$ = ${\dfrac{1}{4}}$
Problem: Solving NEGATIVE EXPONENTS with FRACTIONS
![]()
Simplify ${\left( \dfrac{2}{3}\right) ^{-2}}$
Solution:
![]()
Here, ${\left( \dfrac{2}{3}\right) ^{-2}}$
= $[\dfrac{2^{-2}}{3^{-2}}}$
= ${\dfrac{1}{2^{2}}\times 3^{2}}$
= ${\dfrac{9}{4}}$
Problem: Simplifying NEGATIVE FRACTIONAL EXPONENTS
![]()
Simplify ${\left( \dfrac{8}{27}\right) ^{-\dfrac{2}{3}}}$
Solution:
![]()
Here, ${\left( \dfrac{8}{27}\right) ^{-\dfrac{2}{3}}}$
= ${\left( \dfrac{27}{8}\right) ^{\dfrac{2}{3}}}$
= ${\left( \dfrac{\sqrt[3] {27}}{\sqrt[3] {8}}\right) ^{2}}$
= ${\left( \dfrac{3}{2}\right) ^{2}}$
= ${\dfrac{9}{4}}$
