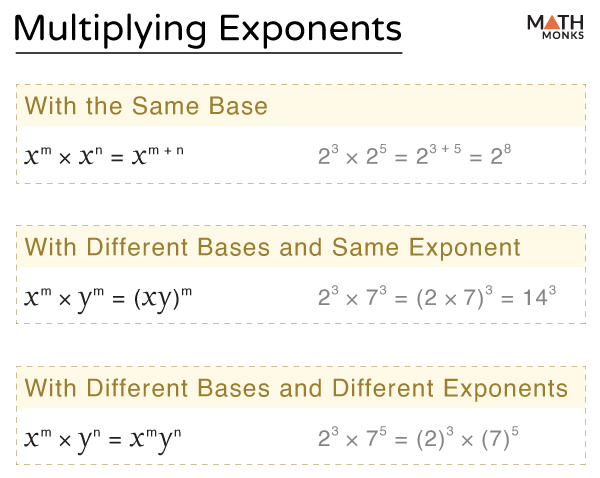Multiplying exponents is when two terms with exponents (also called indices or powers) are multiplied. However, dividing exponents is when two exponential terms are divided.
Multiplying Exponents
There are two possible cases:
With the Same Base
When the terms with the same base are multiplied, the powers are added. Let us multiply two terms: xm and xn. The product is xm × xn = xm + n
For example,
25 × 27 = 25 + 7 = 212
![]()
Multiply 53 × 52
Solution:
![]()
Here, 53 × 52
= 53 + 2
= 55
Problem: Multiplying expressions with VARIABLES
![]()
Multiply a4 × a5
Solution:
![]()
Here, a4 × a5
= a4 + 5
= a9
With Different Bases
When the terms with different bases and the same exponents are multiplied, we multiply the bases by keeping the exponent the same over the product. Let us multiply xm and ym. The product is xm × ym = (xy)m
For example,
25 × 35 = (2 × 3)5 = 65
![]()
Multiply 53 × 73
Solution:
![]()
Here, 53 × 73
= (5 × 7)3
= 353
Problem: Multiplying expressions with VARIABLES
![]()
Multiply a8 × b8
Solution:
![]()
Here, a8 × b8
= (a × b)8
= (ab)8
Different Exponents and Different Bases
When the expressions with different bases and different powers are multiplied, we evaluate each expression separately and then multiply.
Let us multiply xm and yn. The product is xm × yn = xmyn
![]()
Multiply 103 × 32 × 71
Solution:
![]()
Here, 103 × 32 × 71
= 1000 × 9 × 7
= 63000
Negative Exponents
Negative Exponents represent how many times we need to multiply the reciprocal of the base. In other words, a negative exponent can be converted to a positive one by considering the reciprocal of the given term, after which it can be solved just like a positive exponent.
When multiplying negative exponents, we follow the rules given below.
- For the Same Base: ${x^{-m}\times x^{-n}=x^{-\left( m+n\right) }=\dfrac{1}{x^{m+n}}}$
- For Different Bases and the Same Exponent: ${x^{-m}\times y^{-m}=\left( x\times y\right) ^{-m}=\dfrac{1}{\left( x\times y\right) ^{m}}}$
- For Different Bases and Different Exponents: ${x^{-m}\times y^{-n}=x^{-m}y^{-n}=\dfrac{1}{x^{m}y^{n}}}$
![]()
Multiply 3-8 × 9-2 × 3-1
Solution:
![]()
Here, 3-8 × 9-2 × 3-1
= 3-8 × (32)-2 × 3-1
= 3-8 × 3-4 × 3-1
= 3-8 + (-4) + (-1)
= 3-13
Fractional Exponents
When multiplying terms with fractional exponents, we apply the following exponent rules.
- For the Same Base: ${x^{\dfrac{m}{n}}\times x^{\dfrac{p}{q}}=x^{\left( \dfrac{m}{n}+\dfrac{p}{q}\right) }}$
- For Different Bases and the Same Exponent: ${x^{\dfrac{m}{n}}\times y^{\dfrac{m}{n}}=\left( x\times y\right) ^{\dfrac{m}{n}}}$
- For Different Bases and Different Exponents: ${x^{\dfrac{m}{n}}\times y^{\dfrac{p}{q}}=x^{\dfrac{m}{n}}y^{\dfrac{p}{q}}}$
![]()
Multiply ${4^{\dfrac{2}{3}}\times 2^{\dfrac{3}{2}}}$
Solution:
![]()
Here, ${4^{\dfrac{2}{3}}\times 2^{\dfrac{3}{2}}}$
= ${\left( 2^{2}\right) ^{\dfrac{2}{3}}\times 2^{\dfrac{3}{2}}}$
= ${2^{2\times \dfrac{2}{3}}\times 2^{\dfrac{3}{2}}}$
= ${2^{\dfrac{4}{3}}\times 2^{\dfrac{3}{2}}}$
= ${2^{\dfrac{4}{3}+\dfrac{3}{2}}}$
= ${2^{\dfrac{8+9}{6}}}$
= ${2^{\dfrac{17}{6}}}$
Here is a summary of the laws we follow while multiplying expressions with exponents:
Dividing Exponents
Like multiplying exponents, the division of exponents can have two possible cases:
With the Same Base
When the terms with the same base are multiplied, the power of the divisor is subtracted from the power of the dividend.
Let us divide xm by xn. The quotient obtained is xm ÷ xn = ${\dfrac{x^{m}}{x^{n}}=x^{m-n}}$
For example,
${\dfrac{7^{5}}{7^{3}}=7^{5-3}=7^{2}}$
![]()
Evaluate ${\dfrac{4^{5}\times 3^{3}}{4^{2}\times 3^{2}}}$
Solution:
![]()
Here, ${\dfrac{4^{5}\times 3^{3}}{4^{2}\times 3^{2}}}$
= ${\left( \dfrac{4^{5}}{4^{2}}\right) \times \left( \dfrac{3^{3}}{3^{2}}\right)}$
= ${\left( 4^{5-2}\right) \times \left( 3^{3-2}\right)}$
= 43 × 31
= 64 × 3
= 192
With Different Bases
There are two possible cases:
Same Exponents and Different Bases
When the terms with different bases and the same exponents are divided, we divide the bases by keeping the exponent the same over the quotient.
Let us divide xm by ym. The quotient is xm ÷ ym = ${\dfrac{x^{m}}{y^{m}}=\left( \dfrac{x}{y}\right) ^{m}}$
For example,
${\dfrac{7^{3}}{5^{3}}=\left( \dfrac{7}{5}\right) ^{3}}$
![]()
Divide ${\dfrac{4^{5}}{2^{5}}}$
Solution:
![]()
Here, ${\dfrac{4^{5}}{2^{5}}}$
= ${\left( \dfrac{4}{2}\right) ^{5}}$
= 25
Different Exponents and Different Bases
When the expressions with different bases and different powers are divided, we evaluate each expression separately and then divide.
For example,
${\dfrac{2^{5}}{3^{2}}}$ = ${\dfrac{32}{9}}$
![]()
Divide ${\dfrac{3^{3}}{10^{2}}}$
Solution:
![]()
Here, ${\dfrac{3^{3}}{10^{2}}}$
= ${\dfrac{27}{100}}$
= 0.27
Negative Exponents
When dividing negative exponents, we follow the following rules.
- For the Same Base: ${x^{-m}\div x^{-n}=x^{-\left( m-n\right) }=\dfrac{1}{x^{m-n}}}$
- For Different Bases and the Same Exponent: ${x^{-m}\div y^{-m}=\left( \dfrac{x}{y}\right) ^{-m}=\left( \dfrac{y}{x}\right) ^{m}}$
- For Different Bases and Different Exponents: ${x^{-m}\div y^{-n}=\dfrac{x^{-m}}{y^{-n}}=\dfrac{y^{n}}{x^{m}}}$
Fractional Exponents
When multiplying terms with fractional exponents, we apply similar exponent rules.
- For the Same Base: ${x^{\dfrac{m}{n}}\div x^{\dfrac{p}{q}}=x^{\left( \dfrac{m}{n}-\dfrac{p}{q}\right) }}$
- For Different Bases and the Same Exponent: ${x^{\dfrac{m}{n}}\div y^{\dfrac{m}{n}}=\left( \dfrac{x}{y}\right) ^{\dfrac{m}{n}}}$
- For Different Bases and Different Exponents: ${x^{\dfrac{m}{n}}\div y^{\dfrac{p}{q}}=\dfrac{x^{\dfrac{m}{n}}}{y^{\dfrac{p}{q}}}}$
![]()
Divide ${4^{\dfrac{2}{3}}\div 2^{\dfrac{1}{2}}}$
Solution:
![]()
Here, ${4^{\dfrac{2}{3}}\div 2^{\dfrac{1}{2}}}$
= ${\dfrac{4^{\dfrac{2}{3}}}{2^{\dfrac{1}{2}}}}$
= ${\dfrac{\left( 2^{2}\right) ^{\dfrac{2}{3}}}{2^{\dfrac{1}{2}}}}$
= ${\dfrac{2^{2\times \dfrac{2}{3}}}{2^{\dfrac{1}{2}}}}$
= ${\dfrac{2^{\dfrac{4}{3}}}{2^{\dfrac{1}{2}}}}$
= ${2^{\dfrac{4}{3}-\dfrac{1}{2}}}$
= ${2^{\dfrac{8-3}{6}}}$
= ${2^{\dfrac{5}{6}}}$
Here is a summary of the laws we follow while dividing expressions with exponents:
