Factoring polynomials means breaking down a polynomial (with two, three, or more terms) into simpler expressions or factors that, when multiplied together, give back the original polynomial.
For example, the polynomial x2 + 3x + 2 can be factored as (x + 1)(x + 2)
Factoring is useful for simplifying polynomials and for finding the zeros of polynomial functions by setting each factor to zero. For the polynomial x2 + 3x + 2, the zeros are x = -1 and x = -2. Factoring also helps us to analyze the polynomial functions.
Here are the different ways to factor polynomials:
Greatest Common Factor (GCF) Method
This method is the reverse of the distributive law, which states that a(b + c) = ab + ac
For factoring the polynomial ab + ac, we just take out the greatest common factor:
ab + ac = a(b + c), here a is the greatest common factor.
Now, let us factor the polynomial 6x2 + 12x
Finding the GCF of the Terms
6x2 + 12x is a binomial (having 2 terms).
Here, both terms have coefficients that are divisible by 6, and both have at least one x variable, so the GCF, in this case, is 6x.
Thus, the GCF of 6x2 and 12x is 6x
Factoring Out the GCF
6x2 + 12x
= 6x ⋅ x + 6x ⋅ 2
= 6x(x + 2)
Thus, 6x and (x + 2) are the two factors of the polynomial 6x2 + 12x
![]() Factor out the greatest common factor from the polynomial 15x3 – 10x2
Factor out the greatest common factor from the polynomial 15x3 – 10x2
Solution:
![]()
Given, 15x3 – 10x2
Here, the terms are 15x3 and 10x2
The GCF is 5x2
Now, 15x3 – 10x2
= 5x2 ⋅ 3x – 5x2 ⋅ 2
= 5x2(3x – 2)
Thus, 15x3 – 10x2 = 5x2(3x – 2)
Middle-Term Method
For polynomials with 3 terms (trinomials, quadratic, or 2nd-degree polynomials) of the form ax2 + bx + c (here, a ≠ 0), first, we need to find the two numbers that multiply to ac and then add up to b (middle term). We then rewrite the trinomial by breaking down the middle term as ax2 + (m + n)x + c and group the terms to factor.
Here, m + n = b and mn = ac
When a = 1
Let us factor the polynomial x2 – 3x – 10 …..(i)
Comparing With the Standard Form
As we know, the standard form of a trinomial is ax2 + bx + c …..(ii)
Comparing the expressions (i) and (ii), we get
a = 1, b = -3, and c = -10
Thus, ac = (1)(-10) = -10
Finding Two Numbers
Since ac = -10, we need two numbers that multiply to give -10 and add up to -3
Here, -10 = (-5)(2), and b = -3 = -5 + 2
Writing the Trinomial
Now, x2 – 3x – 10
= x2 + (-5 + 2)x + (-5)(2)
= x2 – 5x + 2x – 10
= x(x – 5) + 2(x – 5)
= (x – 5)(x + 2)
Thus, x2 – 3x – 10 is factored as (x – 5)(x + 2)
When a ≠ 1
Let us factor the polynomial 2x2 + 9x + 10 …..(i)
Comparing With the Standard Form
As we know, the standard form of a trinomial is ax2 + bx + c …..(ii)
Comparing the expressions (i) and (ii), we get
a = 2, b = 9, and c = 10
Thus, ac = (2)(10) = 20
Finding Two Numbers
Since 20 = (5)(4) and b = 9 = 5 + 4
Here, the numbers are 5 and 4, which multiply to get 20 and add up to 9.
Writing the Trinomial
Now, 2x2 + 9x + 10
= 2x2 + (5 + 4)x + 10
= 2x2 + 5x + 4x + 10
= x(2x + 5) + 2(2x + 5)
= (2x + 5)(x + 2)
Thus, 2x2 + 9x + 10 = (2x + 5)(x + 2)
Grouping Method
This method is useful for polynomials with four or more terms (known as cubic or 3rd-degree polynomials). To factor a polynomial by grouping, the terms of the given polynomial are grouped in pairs to find the zeroes. The GCF is then factored out from each group.
Let us factor the polynomial x3 + 3x2 + 2x + 6
Grouping the Terms in Pairs
x3 + 3x2 + 2x + 6
= (x3 + 3x2) + (2x + 6)
Factoring Out the GCF From Each Group
= x2(x + 3) + 2(x + 3)
Combining the Factored Groups
= (x + 3)(x2 + 2)
Thus, (x + 3)(x2 + 2) is the factored form of the polynomial x3 + 3x2 + 2x + 6
![]() Write the polynomial 3x3 + 6x2 + 2x + 4 in the factored form.
Write the polynomial 3x3 + 6x2 + 2x + 4 in the factored form.
Solution:
![]()
Given, 3x3 + 6x2 + 2x + 4
= (3x3 + 6x2) + (2x + 4)
= 3x2(x + 2) + 2(x + 2) [Since GCF(3x3, 6x2) = 3x2 and GCF(2x, 4) = 2]
= (x + 2)(3x2 + 2)
Thus, 3x3 + 6x2 + 2x + 4 = (x + 2)(3x2 + 2)
Here is a summary of the different methods of factoring polynomials.
Problem: Factoring Polynomials Using BOX METHOD
The ‘Box or ‘Grid’ method for factoring polynomials is an alternative to the grouping method, especially when the leading coefficient is a ≠ 1 or a ≠ -1
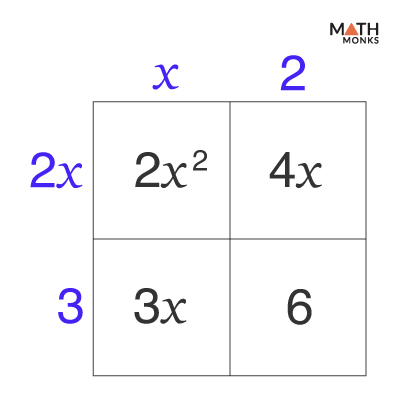
Let us factor the trinomial 2x2 + 7x + 6 …..(i)
Comparing With the Standard Form
As we know, the standard form of a trinomial is ax2 + bx + c …..(ii)
Comparing the expressions (i) and (ii), we get
a = 2, b = 7, and c = 6
Thus, ac = (2)(6) = 12
Finding Two Numbers
Since 12 = (3)(4) and b = 7 = 3 + 4
Here, the numbers are 3 and 4, which multiply to get 12 and add up to 7.
Forming the Box
Here, we place the terms in their corresponding boxes:
- The first term is placed in the upper left box.
- The constant is placed in the lower right box.
- The numbers (found in step 2) with a variable x are then placed in the remaining empty boxes, irrespective of their orders.
Finding the greatest common factor in each row and column
Here,
GCF of the first row is GCF(2x2, 4x) = 2x
GCF of the second row is GCF(3x, 6) = 3
GCF of the first column is GCF (2x2, 3x) = x
GCF of the second column is GCF (4x, 6) = 2
Now, placing them on the side and top of the box, we get
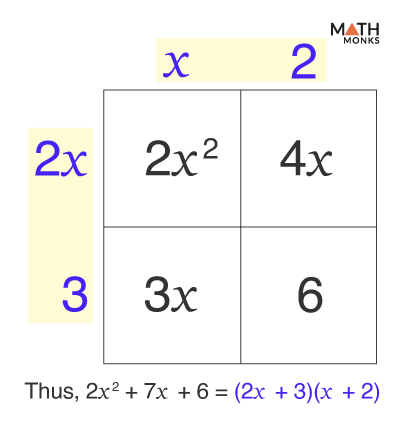
Writing the Polynomial in Factored Form
The first factor is found by adding the terms in the left column, while the second factor is determined by adding the terms in the top row.
Thus, the answer is (2x + 3)(x + 2)
Special Forms – By Using Identities
Some special forms of polynomials can be easily factored using identities.
Factoring Difference of Squares
A polynomial of the form a2 – b2 can be factored as:
Let us factorise the polynomial 9x2 – 49y2 …..(i)
Comparing
Now, comparing (i) with the identity a2 – b2, we get
a2 = 9x2 and b2 = 49y2
⇒ a = 3x and b = 7y
Factoring
Here, 9x2 – 49y2
= (3x)2 – (7y)2
= (3x + 7y)(3x – 7y)
Thus, 9x2 – 49y2 = (3x + 7y)(3x – 7y)
Factoring Perfect Square Trinomials
A perfect square trinomial can be factored into the square of a binomial:
- a2 + 2ab + b2 = (a + b)2
- a2 – 2ab + b2 = (a – b)2
Let us factorise x2 + 6x + 9 …..(i)
Comparing
Comparing equation (i) with the form a2 + 2ab + b2, we get
a2 = x2 and b2 = 9
⇒ a = x and b = 3
Factoring
Here, x2 + 6x + 9
= (x)2 + 2(x)(3) + (3)2
= (x + 3)2
Thus, x2 + 6x + 9 = (x + 3)2 = (x + 3)(x + 3)
Factoring the Sum and Difference of Cubes
Polynomials of the form a3 + b3 and a3 – b3 can be easily factored using the given identities:
- a3 + b3 = (a + b)(a2 – ab + b2)
- a3 – b3 = (a – b)(a2 + ab + b2)
Let us factorise x3 + 27y3 …..(i)
Comparing
Comparing equation (i) with the form a3 + b3, we get
a3 = x3 and b3 = 27y3
⇒ a = x and b = 3y
Factoring
Here, x3 + 27y3
= (x)3 + (3y)3
= (x + 3y)[(x)2 + (x)(3y) + (3y)2]
= (x + 3y)(x2 + 3xy + 9y2)
Thus, x3 + 27y3 = (x + 3y)(x2 + 3xy + 9y2)
![]() Factorise the following polynomials:
Factorise the following polynomials:
a) 8x3 – 125
b) 4x2 – 12x + 9
c) 16x2 – 25
Solution:
![]()
a) Here, 8x3 – 125
= (2x)3 – (5)3
= (2x – 5)[(2x)2 + (2x)(5) + (5)2] [∵ by the difference of cubes, a3 – b3 = (a – b)(a2 + ab + b2)]
= (2x – 5)(4x2 + 10x + 25)
Thus, 8x3 – 125 = (2x – 5)(4x2 + 10x + 25)
b) Here, 4x2 – 12x + 9
= (2x)2 – 2(2x)(3) + (3)2
= (2x – 3)2 [∵ by the perfect square trinomial, a2 – 2ab + b2 = (a – b)2]
= (2x – 3)(2x – 3)
Thus, 4x2 – 12x + 9 = (2x – 3)(2x – 3)
c) Here, 16x2 – 25
= (4x)2 – (5)2
= (4x + 5)(4x – 5) [∵ by the difference of squares, a2 – b2 = (a + b)(a – b)]
Thus, 16x2 – 25 = (4x + 5)(4x – 5)
![]() Which of the following polynomials is factored completely?
Which of the following polynomials is factored completely?
a) 16x2 + 16x + 4 = (4x + 2)2
b) 12x2 – 27 = 3(2x – 3)(2x + 3)
c) 2x2 + 2xy = x(2x + 2y)
Solution:
![]()
Here, option b) is factored completely, as there are no further common factors that can be factored out.