Solving Linear Equations

We can solve linear equations in a number of ways depending on the number of variables and the equations involved.  

A linear equation with a single variable of the form Ax + B = 0 can be easily solved by basic mathematical operations. 

By Addition or Subtraction (For One Variable) 

This method is useful when we are required to use simple addition or subtraction operations to solve for an unknown variable.

Let us solve the equation x + 4 = 2 for x

Step 1: Moving the Constant to the Other Side of the Equation 

First, we will move all constants to the right side of the equation. Here, we will do so by subtracting 4 from both sides.

x + 4 – 4 = 2 – 4  

Step 2: Simplifying to Get the Value of the Variable

⇒ x = 2 – 4

Thus, the solution is x = -4

By Multiplication or Division (For One Variable) 

Sometimes, we need to multiply or divide the variable by a number to isolate the variable. 

Let us solve the equation 4x = 16

Step 1: Making the Coefficient  of the Variable 1

Here, we will divide both sides of the equation by 4 to isolate the variable.

On dividing both sides by 4, we get

⇒ ${\dfrac{4x}{4}=\dfrac{16}{4}}$

Step 2: Solving for the Variable

⇒ x = 4

Thus, the solution is x = 4

Note: There are many methods for solving linear equations involving 2 or more variables.

By Substitution (For Two or More Variables) 

This method is ideal for solving systems of two linear equations when one equation is already solved for a variable.

Let us solve the system

2x + y = 10 …..(i)

x – y = 2 …..(ii)

Step 1: Expressing One Variable in Terms of the Other

From the equation (ii),

x – y = 2

⇒ x = y + 2

Step 2: Substituting Into the First Equation

2x + y = 10

⇒ 2(y + 2) + y = 10

⇒ 2y + 4 + y = 10

⇒ 2y + y = 10 – 4

Step 3: Solving for y

⇒ 3y = 6

⇒ y = 2

Step 4: Finding x

Now, substituting y = 2 back into the equation x = y + 2,

x = 2 + 2 = 4

Thus, the solution is: x = 4 and y = 2

By Elimination (For Two or More Variables) 

In this method, we first add or subtract equations to eliminate one variable to get the value of the other variable. 

Let us solve the equations:

3x + 2y = 12 …..(i)

2x – 2y = 4 …..(ii)

Step 1: Identifying the Variable For Eliminating It 

Here, the y-terms in both equations have the opposite coefficients: 

+2y in equation (i) and -2y in equation (ii)

Here is no need to multiply any constant value by the given equations.

Step 2: Adding the equations 

(3x + 2y) + (2x – 2y) = 12 + 4

⇒ 3x + 2y + 2x – 2y = 16

⇒ 3x + 2x = 16

⇒ 5x = 16

Step 3: Solving for x 

⇒ x = ${\dfrac{16}{5}}$

Step 4: Substituting x Into One of the Original Equations 

3x + 2y = 12

⇒ ${3\left( \dfrac{16}{5}\right) +2y=12}$

⇒ ${\dfrac{48}{5}+2y=12}$

⇒ ${2y=12-\dfrac{48}{5}}$

⇒ ${2y=\dfrac{60-48}{5}}$

⇒ ${2y=\dfrac{12}{5}}$

⇒ ${y=\dfrac{6}{5}}$

Thus, the solution is: x = y=\dfrac{12}{5}}$ and y = ${\dfrac{6}{5}}$

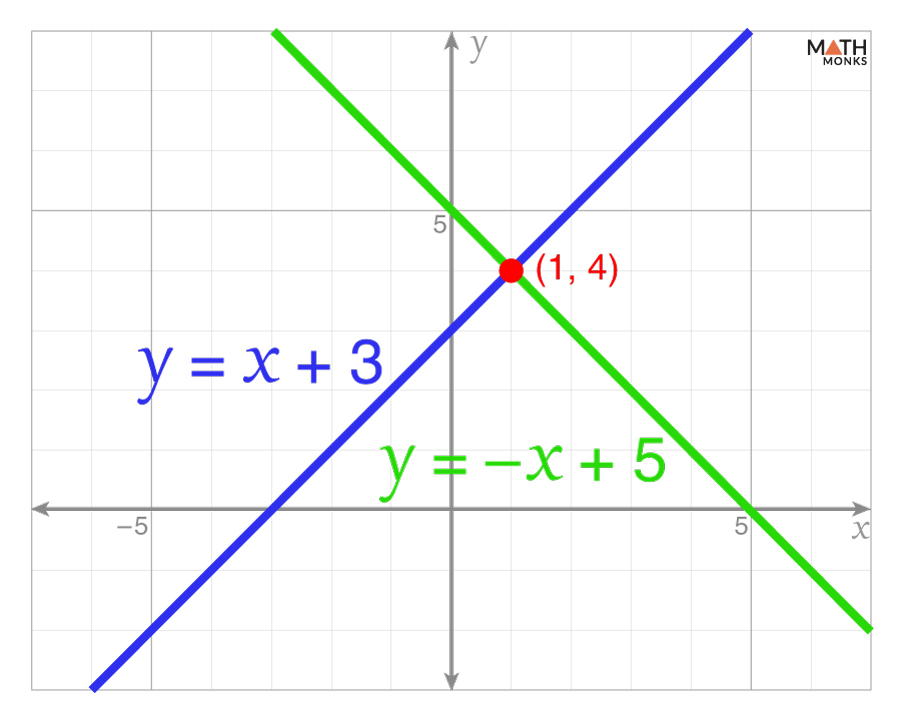
By Graph (For Two or More Variables) 

This method is useful when we want to visualize the solution. 

Here, we plot each equation on a coordinate plane and find their intersection point, which is the solution.

Let us consider the system:

y = x + 3 …..(i)

y = -x + 5 …..(ii)

Step 1: Plotting Both Equations on a Graph 

In the equation (i),

Slope = 1 

Y-intercept = 3

In the equation (ii),

Slope = -1

Y-intercept = 5

When plotting equations (i) and (ii), we get

Step 2: Finding the Intersection Point 

In the graph, the intersection point of both lines will be the solution of the given equations. Here, the intersection point is (x, y) = (1, 4)

Thus, the solution of the given system is x = 1 and y = 4

By Cross-Multiplication (For One or Two Variables)

We particularly use this method when the equations are present in fractional form. 

Here, first, we multiply both sides by the denominator to eliminate fractions and then solve for the variable.

Let us solve the equation ${\dfrac{2x+3}{5}=\dfrac{4}{7}}$ for the given variable:

Step 1: Identifying the Equation in Proportion Form

The given equation is already in the form of a proportion: ${\dfrac{a}{b}=\dfrac{c}{d}}$

Step 2: Multiplying both sides by the Denominator

Here, ${\dfrac{2x+3}{5}=\dfrac{4}{7}}$

⇒ 7(2x + 3) = 5(4)

⇒ 14x + 21 = 20

Step 3: Solving for the Variable

⇒ 14x + 21 – 21 = 20 – 21

⇒ 14x = -1

⇒ ${\dfrac{14x}{14}=\dfrac{-1}{14}}$

⇒ x = ${\dfrac{-1}{14}}$

Thus, the solution is x = ${\dfrac{-1}{14}}$

For solving a system involving 2 variables by cross-multiplication method, the general formula is:

${\dfrac{x}{b_{1}c_{2}-b_{2}c_{1}}=\dfrac{y}{c_{1}a_{2}-c_{2}a_{1}}=\dfrac{1}{b_{2}a_{1}-b_{1}a_{2}}}$

Let us consider the following system of linear equations:

x + 3y = -3 …..(i)

2x – y = 9 …..(ii)

Step 1: Identifying Coefficients

Comparing with the standard form a₁x + b₁y = c₁ and a₂​x + b₂y = c₂, we have:

a₁ = 1, b₁ = 3, c₁ = -3

a₂ = 2, b₂ = -1, c₂ = 9

Step 2: Applying the Cross-Multiplication Formula

Now, by using the formula, we get

${\dfrac{x}{\left( 3\right) \left( 9\right) -\left( -1\right) \left( -3\right) }=\dfrac{y}{\left( -3\right) \left( 2\right) -\left( 9\right) \left( 1\right) }=\dfrac{1}{\left( -1\right) \left( 1\right) -\left( 3\right) \left( 2\right) }}$

⇒ ${\dfrac{x}{27-3}=\dfrac{y}{-6-9}=\dfrac{1}{-1-6}}$

⇒ ${\dfrac{x}{24}=\dfrac{y}{-15}=\dfrac{1}{-7}}$

Thus, the solutions are: x = ${-\dfrac{24}{7}}$ and y = ${\dfrac{15}{7}}$

Note: Apart from these methods, linear equations with three or more variables can also be solved using the matrix method (by inverse matrix method and Gaussian elimination) and the determinants method (by Cramer’s rule).

Solved Examples