A linear equation is an equation that represents a straight line when graphed. It typically has one or two variables and follows the general form ax + b = c or ax + by = c, where x is the unknown variable, and a, b, and c are constants.
In this article, we will solve some real-life problems by representing them as linear equations and then find their solutions.
![]()
John is 5 years older than Sarah. If the sum of their ages is 25 years, how old is each of them?
Solution:
![]()
Let Sarah’s age be x
John’s age = x + 5
By the problem, the sum of their ages is:
x + (x + 5) = 25
⇒ x + x + 5 = 25
⇒ 2x + 5 = 25
Solving,
⇒ 2x = 25 – 5
⇒ 2x = 20
⇒ x = 10
Thus, Sarah is 10 years old, and John is 15 years old.
![]()
A shop sells pens for \$2 each and notebooks for \$5 each. A customer buys 3 pens and some notebooks, spending a total of \$21. How many notebooks did they purchase?
Solution:
![]()
Let x be the number of notebooks.
By the problem, the total cost equation is:
2(3) + 5(x) = 21
⇒ 6 + 5x = 21
Solving,
⇒ 5x = 21 – 6
⇒ 5x = 15
⇒ x = 3
Thus, the customer bought 3 notebooks.
![]()
A farmer mixes 10 kg of corn, priced at $4 per kg, with an unknown amount of wheat, priced at $6 per kg. The final mixture weighs 20 kg and has an average cost of $5 per kg. How much wheat was added?
Solution:
![]()
Let x be the amount of wheat added.
By the problem, the total cost equation is:
4(10) + 6(x) = 5(20)
⇒ 40 + 6x = 100
Solving,
⇒ 6x = 100 – 40
⇒ 6x = 60
⇒ x = 10
Thus, 10 kg of wheat was added.
![]()
The sum of two numbers is 36. One number is twice the other. Find the numbers.
Solution:
![]()
Let the smaller number be x.
The second number is 2x.
By the problem, the sum of two numbers is:
x + 2x = 36
Solving,
⇒ 3x = 36
⇒ x = 12
Here, the smaller number is 12, and the larger number is 2(12) = 24
Thus, the two numbers are 12 and 24.
![]()
A chemist combines 5 liters of a 10% alcohol solution with an unknown amount of a 30% alcohol solution. The final mixture is 15 liters with an alcohol concentration of 20%. How much of the 30% solution was used?
Solution:
![]()
Let x be the amount of 30% alcohol solution mixed.
By the problem, the total alcohol in the solution is:
(5 × 0.10) + (x × 0.30) = (15 × 0.20)
⇒ 0.5 + 0.3x = 3
Solving,
⇒ 0.3x = 3 – 0.5
⇒ 0.3x = 2.5
⇒ x = ${\dfrac{2.5}{0.3}}$
⇒ x = 8.33
Thus, the chemist used 8.33 liters of the 30% alcohol solution.
![]()
A train travels 240 miles at a certain speed. If the speed were increased by 20 mph, the journey would take 1 hour less. What was the train’s original speed?
Solution:
![]()
Let the original speed of the train be x mph
Time taken at speed x mph is ${\dfrac{240}{x}}$
Time taken at speed (x + 20) mph is ${\dfrac{240}{x+20}}$
By the problem, if the speed were (x + 20) mph, the journey would take time:
${\dfrac{240}{x+20}=\dfrac{240}{x}-1}$
⇒ ${\dfrac{240}{x}-\dfrac{240}{x+20}=1}$
⇒ ${\dfrac{240\left( x+20\right) -240x}{x\left( x+20\right) }=1}$
⇒ 240(x + 20) – 240x = x(x + 20)
⇒ 240x + 4800 – 240x = x2 + 20x
⇒ 4800 = x2 + 20x
⇒ x2 + 20x – 4800 = 0
By using the quadratic formula,
x = ${\dfrac{-20\pm \sqrt{\left( 20\right) ^{2}-4\left( 1\right) \left( -4800\right) }}{2\left( 1\right) }}$
⇒ x = ${\dfrac{-20\pm \sqrt{400+19200}}{2}}$
⇒ x = ${\dfrac{-20\pm \sqrt{19600}}{2}}$
⇒ x = ${\dfrac{-20\pm 140}{2}}$
⇒ x = 60 and -80
Since speed cannot be negative, the original speed of the train is 60 mph
![]()
Workers A and B can together complete a job in 10 days. However, A alone takes 4 days less than B to finish the job. How many days does each worker take to complete the job individually?
Solution:
![]()
Let B take x days to complete the job alone.
Then, A takes (x – 4) days
Work done by A in one day is ${\dfrac{1}{x-4}}$ of the job
Work done by B in one day is ${\dfrac{1}{x}}$ of the job
Together, they complete the job in 10 days.
According to the problem, their combined work per day is:
${\dfrac{1}{x-4}+\dfrac{1}{x}=\dfrac{1}{10}}$
⇒ ${\dfrac{x+x-4}{x\left( x-4\right) }=\dfrac{1}{10}}$
⇒ 10(2x – 4) = x(x – 4)
⇒ 20x – 40 = x2 – 4x
⇒ x2 – 4x – 20x + 40 = 0
⇒ x2 – 24x + 40 = 0
By using the quadratic formula,
x = ${\dfrac{-\left( -24\right) \pm \sqrt{\left( -24\right) ^{2}-4\left( 1\right) \left( 40\right) }}{2\left( 1\right) }}$
⇒ x = ${\dfrac{24\pm \sqrt{576-160}}{2}}$
⇒ x = ${\dfrac{24\pm \sqrt{416}}{2}}$
Since ${\sqrt{416}}$ ≈ 20.40
⇒ x = ${\dfrac{24\pm 20.40}{2}}$
⇒ x = 1.8 and 22.2
Since x represents the number of days B takes to complete the job, it must be a reasonable value.
The smaller root (x = 1.8) is not valid because A would take negative days, which is impossible.
Thus, the valid solution is:
B takes approximately 22.2 days to complete the job alone, and A takes 22.2 – 4 = 18.2 days to complete the job alone.
![]()
Two companies, Company A and Company B, manufacture the same product. Company A has a fixed cost of $5000 and a variable cost of $20 per unit, while Company B has a fixed cost of $3000 and a variable cost of $30 per unit. At what production level will the total cost for both companies be the same?
Solution:
![]()
Let x be the number of units produced.
Total cost for Company A = Fixed cost + (Variable cost per unit × Number of units)
⇒ CA = 5000 + 20x
Total cost for Company B = Fixed cost + (Variable cost per unit × Number of units)
⇒ CB = 3000 + 30x
By the problem, the number of units where both companies have the same total cost:
5000 + 20x = 3000 + 30x
⇒ 5000 – 3000 = 30x – 20x
⇒ 2000 = 10x
⇒ x = 200
Thus, the total costs of Company A and Company B will be the same when they each produce 200 units.
![]()
A delivery company charges a base fee of \$5 plus \$2 per mile for delivering packages. If x is the number of miles traveled, and y is the total delivery cost, then:
a) Write a linear equation to represent this situation.
b) Graph the equation.
c) What is the cost of a delivery for a 6-mile trip?
Solution:
![]()
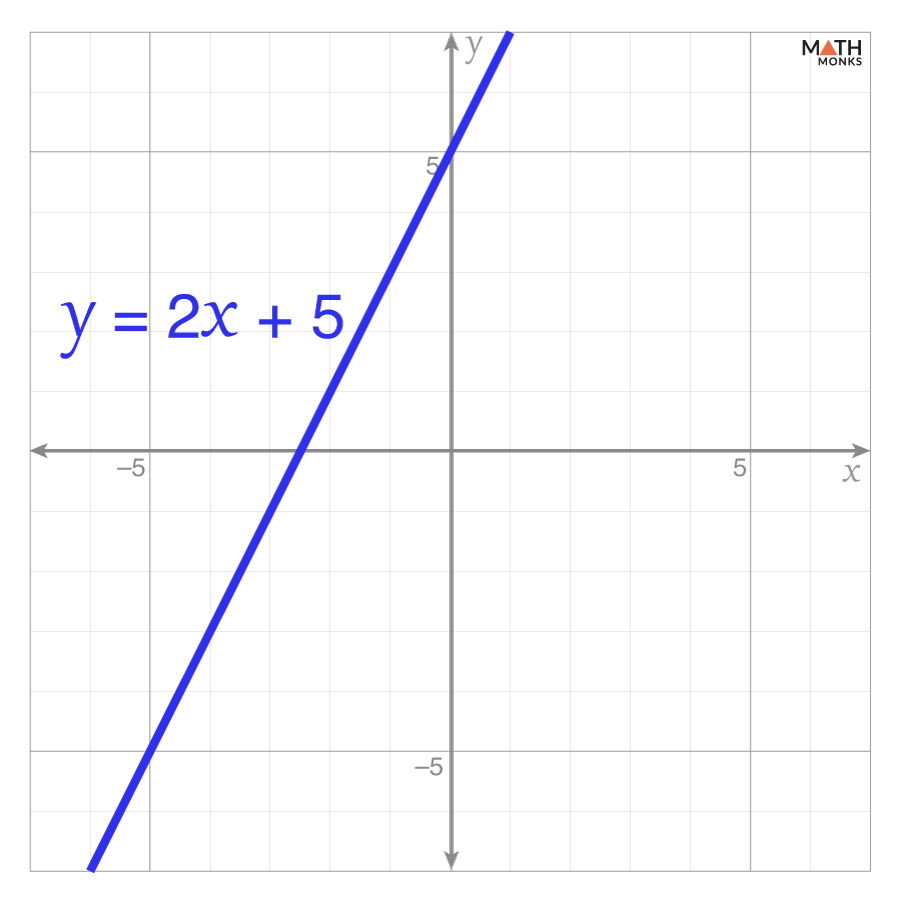
Let x be the number of miles traveled, and y be the total delivery cost
By the problem, a delivery company charges a base fee of \$5 plus \$2 per mile for delivering packages.
a) Thus, the cost equation is: y = 2x + 5
b) After plotting the equation y = 2x + 5, we get the required graph.
c) Substituting x = 6 into the equation,
y = 2(6) + 5
⇒ y = 12 + 5
⇒ y = 17
Thus, the cost for a 6-mile delivery is \$17.
