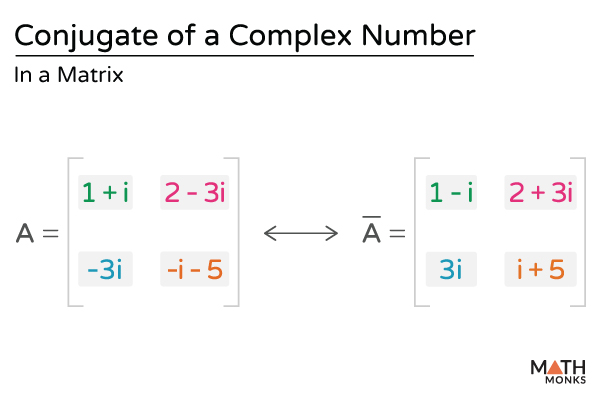Conjugate of a Complex Number

The conjugate of a complex number a+ib, where a and b are real numbers, is written as a−ib. It involves changing the sign of the imaginary part, resulting in a new complex number with the same real part but an imaginary part with the opposite sign.

Mathematically, for the complex number z = a + ib, its complex conjugate is ${\overline{z}}$ = a – ib, and the complex conjugate of ${\overline{z}}$ is z.

Thus, z and ${\overline{z}}$ are a complex-conjugate pair.

For example,

The complex conjugate of:

3 – i is ${\overline{3-i}}$ = 3 + i,

-4 + 6i is ${\overline{-4+6i}}$ = -4 – 6i, and

7i is ${\overline{7i}}$ = -7i.

Graphing Complex Conjugates

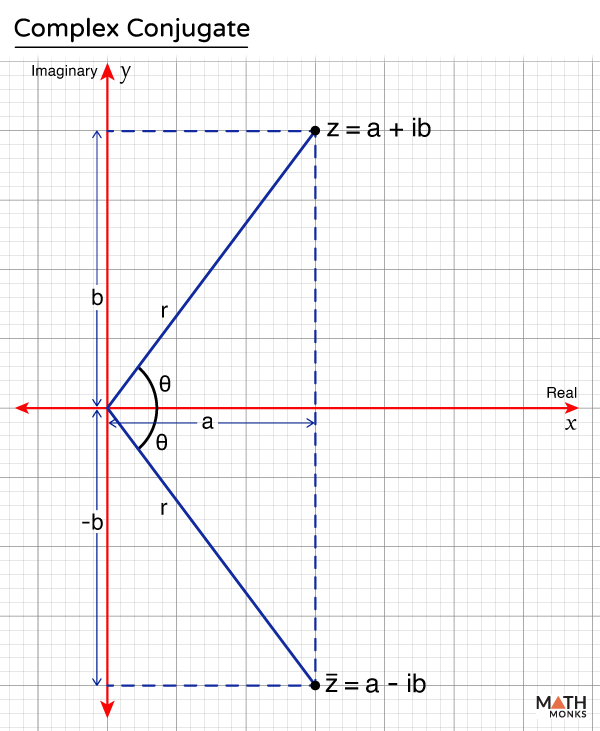
The complex conjugate gives the mirror image of the complex number z = a + ib in the argand plane, as shown. 

Here, z lies in the first quadrant, whereas its image ${\overline{z}}$ = a – ib is in the fourth quadrant with respect to the horizontal axis (x-axis).

When the complex number is represented in the polar form of z = re^iθ, its conjugate is re^-iθ.

Properties

• The conjugate of any purely real complex number is the number itself; z = ${\overline{z}}$.

• The conjugate of any purely imaginary number is the negative value of that number. If z = ${-\overline{z}}$ then, z + ${\overline{z}}$ = 0.
• The conjugate of the product of any two complex numbers equals the product of their conjugates, that is, ${\overline{zw}=\overline{z}\cdot \overline{w}}$.
• The conjugate of the quotient of any two complex numbers equals the quotient of their conjugates, that is, ${\overline{\left( \dfrac{z}{w}\right) }}$ = ${\dfrac{\overline{z}}{\overline{w}}}$, where w ≠ 0. 
• On adding two complex numbers z and w, the conjugate of their sum equals the quotient of their conjugates, that is, ${\overline{z+w}}$ = ${\overline{z}+\overline{w}}$

• If a number w is subtracted from another number z, then the conjugate of their sum equals the quotient of their conjugates, that is, ${\overline{z-w}}$ = ${\overline{z}-\overline{w}}$.
• The difference between a complex number and its conjugate gives twice the imaginary part of the complex number, that is, z – ${\overline{z}}$ = ${2\cdot Im\left( z\right)}$.
• The product of a pair of complex conjugates z and ${\overline{z}}$ equals the square of the absolute value of the complex number, that is, ${z\cdot \overline{z}}$ = {Re(z)}² + {Im(z)}² = |z|².

Multiplication 

When we multiply a complex number by its conjugate, the result is always a real number.

For the complex number z = a + ib, its conjugate is ${\overline{z}}$ = a – ib

Now, on multiplying the complex number z by its conjugate ${\overline{z}}$, we get

(a + ib)(a – ib) = a(a – ib) + ib(a – ib) = a² – i²b²

Substituting the value i² = -1, the product is (a + ib)(a – ib) = a² + b²

Thus, the product is a real number that equals the square of the complex number’s absolute value.

Let us consider another example. If 2 + 3i is a  complex number, on multiplying by its conjugate number 2 – 3i, we get

(2 + 3i)(2 – 3i) = 2² – (3i)² = 2² – 9i² = 4 + 9 = 13 = |2 + 3i|², which is again a real number.

Addition 

Similarly, the sum is always a real number while adding a complex number by its conjugate.

Let us consider z = -3 + 5i, and its conjugate ${\overline{z}=-3-5i}$.

Adding these two numbers, we get ${z+\overline{z}}$ = (-3 + 5i) + (-3 – 5i)

= -3 + 5i – 3 – 5i = (-3 – 3) + (5i – 5i) = -6 = 2(-3), which is twice the real part of z.

Thus, we conclude that the sum of a complex number and its conjugate gives twice the real part of the complex number.

Conjugate Roots in Polynomial

If f(x) is a polynomial in which coefficients are real and a + ib is one of its roots, then its complex conjugate a – ib is also a root of f(x).

Let us understand this theorem with an example of polynomial f(x) = x³ – 11x² + 40x – 50.

Here, the roots of the above polynomial are 5, -3 + i, -3 – i. Since -3 + i and -3 – i are the complex conjugates of each other, we conclude that the complex roots of any polynomial come in a pair.

Conjugate of Matrix

We can determine the complex conjugate of any matrix by calculating the complex conjugate of each individual matrix entry. 

For example, a matrix A = ${\begin{bmatrix} a+ib & pi \\ c-id & -x+iy \end{bmatrix}}$. 

Thus, the complex conjugate of the matrix A is ${\overline{A}}$ = ${\begin{bmatrix} a-ib & -pi \\ c+id & -x-iy \end{bmatrix}}$

Now, let us consider another example of a matrix and determine its complex conjugate.

Solved Examples