Cycloid

A cycloid (referred to as ‘the Helen of geometers’) is a curve formed by tracing the path of a fixed point on the circumference of a circle when it rolls along a straight line without slipping. 

This curve was first studied and named by Galileo in 1599.

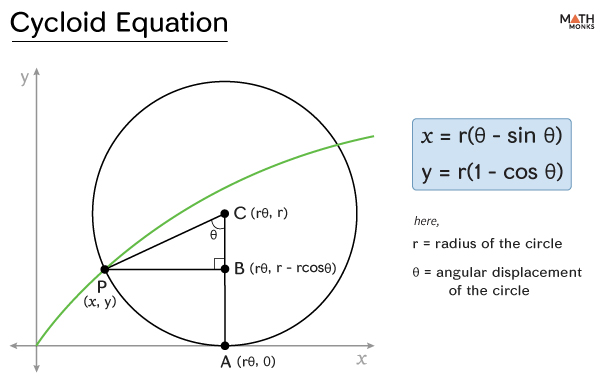
Here, the cycloid is represented by the green curve traced by a point on the circle’s outer edge as it moves along a straight line.

Equation

The equation of a cycloid can be written in parametric and cartesian forms.

Parametric Form

The equation of a cycloid is written in parametric or polar form as:

• x = r(θ – sin θ)
• y = r(1 – cos θ)

Here,

• r = the radius of the circle 
• θ = the angular displacement of the circle

These parametric equations describe the xy coordinates of the point on the circle with respect to r and θ when it rolls. The distance between each point where the curve touches the straight line is 2πr (i.e., the circumference of the circle), representing one full revolution of the circle. 

Since the cycloid repeats its shape after each cycle, it is known as a periodic curve with a repeating length of 2πr.

Derivation

Let us consider the left part of the cycloid (shown in green) generated by the circle after it has rotated by θ radians.

With C as the center of the circle, two radii are drawn: one to the point (x,y) on the cycloid and the other to a point A on the x-axis. 

Now, the x-coordinate of A and C is defined by the arc length between them, which is r ⋅ θ

Next, a perpendicular is drawn from point P to the line AC, intersecting AC at point B. 

By applying the definition of trigonometry to triangle PCB, we derive the following:

sinθ = ${\dfrac{length \  of \  \overline{PB}}{r}}$ and cosθ = ${\dfrac{length \  of \  \overline{BC}}{r}}$

⇒ length of ${\overline{PB}}$ = r ⋅ sinθ and length of ${\overline{BC}}$ = r ⋅ cosθ

Substituting these values, the coordinates of point P are:  

The x-coordinate of P = r ⋅ θ – the length of ${\overline{PB}}$ 

The y-coordinate of P = r – the length of ${\overline{BC}}$ 

After factoring, we obtain the parametric equations for P as:

• x = r(θ – sin θ)
• y = r(1 – cos θ)

Here, r is the radius of the circle, and θ is the angular displacement of the circle in radians. 

Cartesian Form

In Cartesian coordinates, the equation of cycloid is expressed as:

${x=r\arccos \dfrac{r-y}{r}-\sqrt{2ry-y^{2}}}$

Here, r = the radius of the circle.

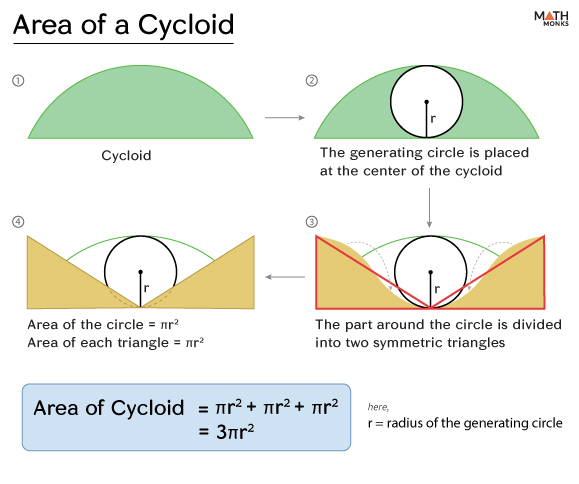
Area

If the radius of the generating circle is r, the base length of one cycloid arch is 2πr.

Now, let us consider the circle at the center of the cycloid.

Using 2D Cavalieri’s principle, the area around the circle is symmetrically divided into two triangles. If these areas are shifted horizontally, their total area remains unchanged.

According to symmetry, these regions correspond to two triangles and two circles, as shown.

By Integration

The area under each arch of the cycloid can also be found using the integration formula:

${A=\int ^{b}_{a}ydx}$ …..(i)

As we know, x = r(θ – sin θ) and y = r(1 – cos θ)

⇒ dx = r(1 – cos θ) dθ and y = r(1 – cos θ) …..(ii)

Now, by substituting (ii) in (i), we get

${A=\int ^{2\pi }_{0}r\left( 1-\cos \theta \right) \cdot r\left( 1-\cos \theta \right) d\theta}$

= ${r^{2}\int ^{2\pi }_{0}\left( 1-\cos \theta \right) ^{2}\cdot d\theta}$

= ${r^{2}\int ^{2\pi }_{0}\left( 1-2\cos \theta +\cos ^{2}\theta \right) d\theta}$

= ${r^{2}\int ^{2\pi }_{0}\left( 1-2\cos \theta +\dfrac{\cos 2\theta +1}{2}\right) d\theta}$

= ${r^{2}\left[ \dfrac{3\theta }{2}-2\sin \theta +\dfrac{\sin 2\theta }{4}\right] _{0}^{2\pi }}$

= ${r^{2}\left[ \dfrac{3\left( 2\pi \right) }{2}\right]}$

= 3πr²

Thus, the area under an arch of the cycloid is 3πr² (3 times the area of the generating circle).

Arc Length

To find the arc length of each arch of the cycloid, we will apply the arc length formula of a curve in parametric form:

${L=\int ^{b}_{a}\sqrt{\left( \dfrac{dx}{d\theta }\right) ^{2}+\left( \dfrac{dy}{d\theta }\right) ^{2}}d\theta}$ …..(i)

As we know, x = r(θ – sin θ) and y = r(1 – cos θ)

⇒ ${\dfrac{dx}{d\theta }=r\left( 1-\cos \theta \right)}$ and 

${\dfrac{dy}{d\theta }=r\sin \theta}$ …..(ii)

Now, by substituting the values of (ii) in (i), we get

${L=\int ^{2\pi }_{0}\sqrt{r^{2}\sin ^{2}\theta +r^{2}\left( 1-\cos \theta \right) ^{2}}d\theta}$

= ${r\int ^{2\pi }_{0}\sqrt{2-2\cos \theta }d\theta}$

= ${\sqrt{2}r\int ^{2\pi }_{0}\sqrt{1-\cos \theta }d\theta}$

= ${\sqrt{2}r\int ^{2\pi }_{0}\sqrt{2}\sin \dfrac{\theta }{2}d\theta}$

= ${-4r\left[ \cos \dfrac{\theta }{2}\right] _{0}^{2\pi }}$

= -4r(-1 – 1)

= 8r

Thus, the arc length of a single cycloidal arch is 8r (8 times the radius of the generating circle).

Volume

If an arch of the cycloid is rotated around the x-axis, the volume of the solid formed by that arch is:

${V=\pi \int ^{b}_{a}y^{2}dx}$ …..(i)

Now, using y = r(1 – cos θ) and dx = r(1 – cos θ) dθ in the equation (i), we get

${V=\pi \int ^{b}_{a}r^{2}\left( 1-\cos \theta \right) ^{2}\cdot r\left( 1-\cos \theta \right) d\theta}$

= ${\pi \int ^{b}_{a}r^{3}\left( 1-\cos \theta \right) ^{3}d\theta}$

= ${5\pi ^{2}r^{3}}$

If the arch is rotated around the y-axis, the volume of the solid formed by that arch is:

${2\pi \Upsilon \int ^{2\pi }_{0}\left( \theta -\sin \theta \right) \left( 1-\cos \theta \right) ^{2}d\theta}$ = ${6\pi ^{3}r^{3}}$

Types

Based on the nature of the tracing point and rolling circle, cycloids can be classified into the following types: 

Curtate Cycloid

Also known as a contracted cycloid, it is formed by a point inside the rolling circle, which is closer to the center than the edge. Since the point is inside the circle, the curved path has loops and touches below the line at its cusps. 

The parametric equations of a curtate cycloid are: 

• x = r(θ – a sin θ)
• y = r(1 – a cos θ)

Here, 0 < a < 1, and a = the distance from the center of the circle to the tracing point.

Prolate Cycloid 

It is formed by a point outside the circle, which is closer to the edge than the center. Here, the curved path has no cusps and no intersecting lines.

The parametric equations of a prolate cycloid are:

• x = r(θ – a sin θ)
• y = r(1 – a cos θ)

Here, a > 1, and a = the distance from the center of the circle to the tracing point.

Epicycloid 

It forms when a circle rolls along the outside of another circle’s circumference (called a stationary circle). The curved path has distinct rounded loops.

The parametric equations of an epicycloid are:

• ${x=\left( R+r\right) \cos \theta -r\cos \left( \dfrac{R+r}{r}\theta \right)}$
• ${y=\left( R+r\right) \sin \theta -r\sin \left( \dfrac{R+r}{r}\theta \right)}$

Here, r = the radius of the generating circle, and R = the radius of the stationary circle. 

Hypocycloid 

It is formed when a circle rolls along the inside of another circle’s circumference (called a stationary circle). The shape of the hypocycloid varies depending on the size ratio of the two circles, and it can sometimes have sharp cusps or pointed edges.

The parametric equations of a hypocycloid are:

• ${x=\left( R-r\right) \cos \theta +r\cos \left( \dfrac{R-r}{r}\theta \right)}$
• ${y=\left( R-r\right) \sin \theta -r\sin \left( \dfrac{R-r}{r}\theta \right)}$

Here, r = the radius of the generating circle, and R = the radius of the stationary circle.