In Euclidean geometry, the distance formula is used to find the distance between two points on a coordinate plane. If the points are on the same vertical or horizontal line, the distance between the points is calculated by subtracting their coordinates, which is given by the distance formula.
It is derived from the Pythagorean theorem, which is commonly used to find the distance between two points in a 2-dimensional (2-D) plane.
Formula
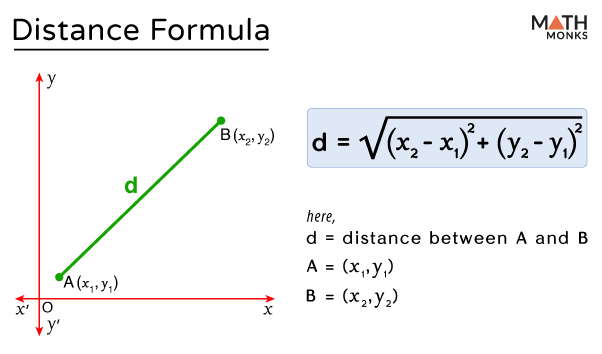
The distance between the points A (x1, y1) and B (x2, y2) is given by the euclidean distance formula as:
${d=\sqrt{\left( x_{2}-x_{1}\right) ^{2}+\left( y_{2}-y_{1}\right) ^{2}}}$
Derivation
It is derived from the Pythagorean theorem as follows:
Let us plot the points A (x1, y1) and B (x2, y2) on the coordinate plane.
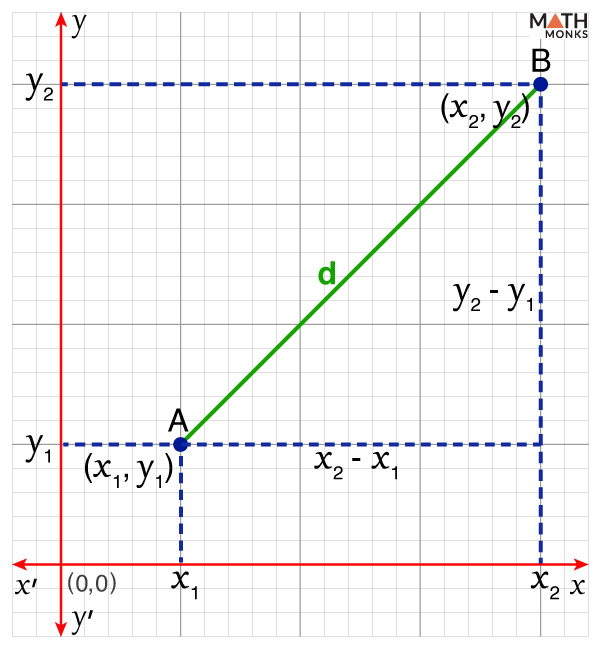
The length between the points ‘A’ and ‘B’ is the distance between them (say ‘d’). By joining the points ‘A’ and ‘B,’ we get a line segment AB.
Now, to find the distance ‘d,’ we will calculate the hypotenuse AB in the triangle ABC.
From the above graph, the length of AC and BC is written as:
AC = (x2 – x1) and BC = (y2 – y1)
Now, using the Pythagoras theorem to calculate the length AB, we get
AB2 = AC2 + BC2
⇒ d2 = (x2 – x1)2 + (y2 – y1)2
Taking the square root of both sides,
${d=\sqrt{\left( x_{2}-x_{1}\right) ^{2}+\left( y_{2}-y_{1}\right) ^{2}}}$, the formula of the distance between two points.
Now, let us find the distance between two points A (3, 5) and B (7, 8)
Here,
x1 = 3,
y1 = 5,
x2 = 7, and
y2 = 8
Thus, the distance = ${d=\sqrt{\left( x_{2}-x_{1}\right) ^{2}+\left( y_{2}-y_{1}\right) ^{2}}}$
= ${\sqrt{\left( 7-3\right) ^{2}+\left( 8-5\right) ^{2}}}$
= ${\sqrt{\left( 4\right) ^{2}+\left( 3\right) ^{2}}}$
= ${\sqrt{16+9}}$
= ${\sqrt{25}}$
= 5 units
Thus, the distance between two points A (3, 5) and B (7, 8) is 5 units.
![]() Find the distance between the two points P(-10, 15) and Q (5, 5)
Find the distance between the two points P(-10, 15) and Q (5, 5)
Solution:
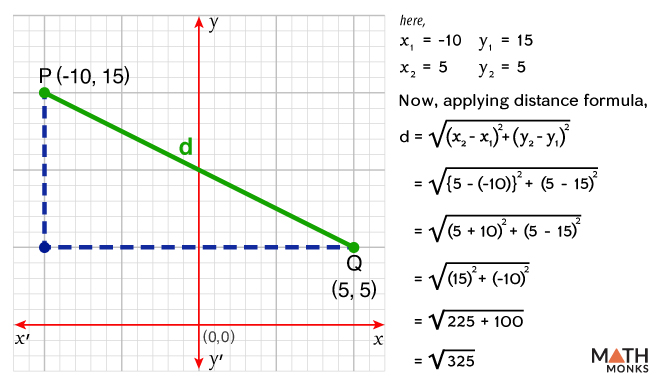
Thus, the distance between two points P (-10, 15) and Q (5, 5) is ${\sqrt{325}}$ units.
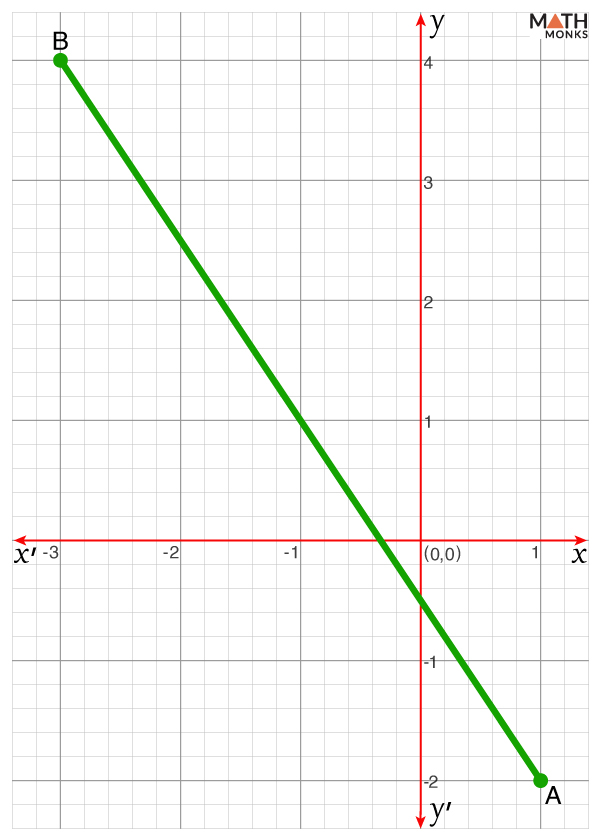 Find the distance between two points ‘A’ and ‘B’ in the given figure.
Find the distance between two points ‘A’ and ‘B’ in the given figure.
Solution:
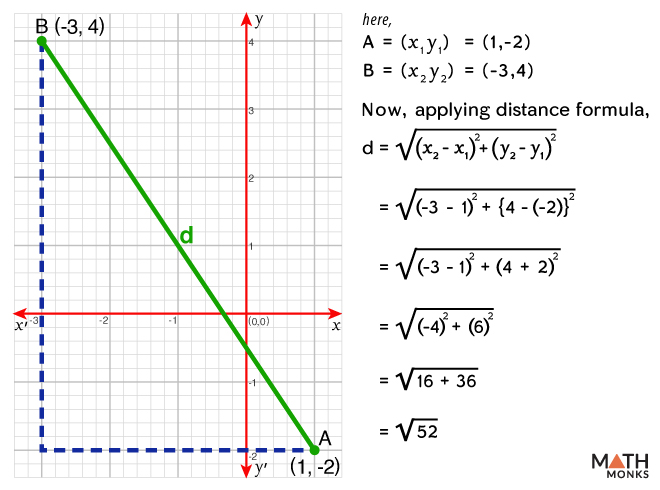
Thus, the distance between two points ‘A’ and ‘B’ is ${\sqrt{52}}$ units.
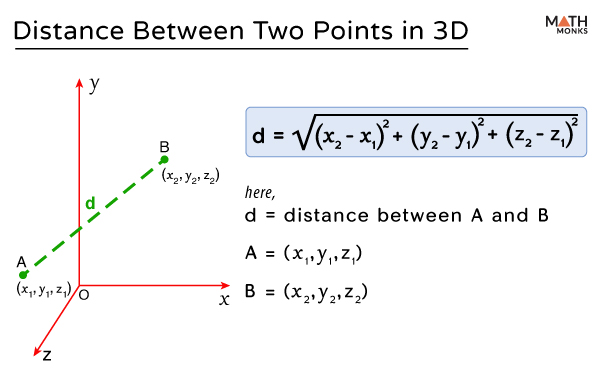
Distance between Two Points in a 3D Plane
Apart from calculating the distance between two points in a 2-D plane, the distance formula is also used to calculate their distance in a three-dimensional (3-D) plane. If we consider two points A (x1, y1, z1) and B (x2, y2, z2) in a three-dimensional plane, then the distance between the points is given by:
${d=\sqrt{\left( x_{2}-x_{1}\right) ^{2}+\left( y_{2}-y_{1}\right) ^{2}+\left( z_{2}-z_{1}\right) ^{2}}}$
Distance From a Point To a Line
While calculating the distance from a point to a line in 2D and 3D planes, we use the following formulas:
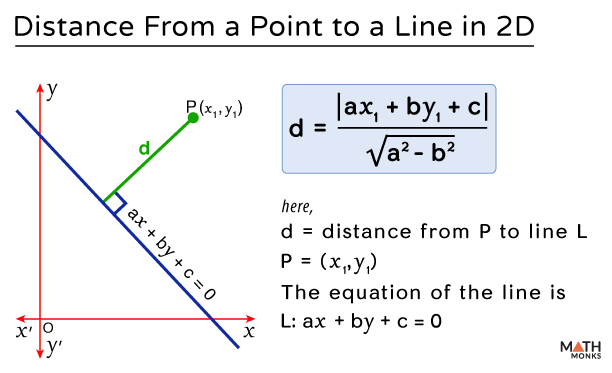
In a 2D Plane
The distance ‘d’ from the point P (x1, y1) to the line ‘L’ (with the equation ax + by + c = 0) is given by
${d=\dfrac{\left| ax_{1}+by_{1}+c\right| }{\sqrt{a^{2}+b^{2}}}}$
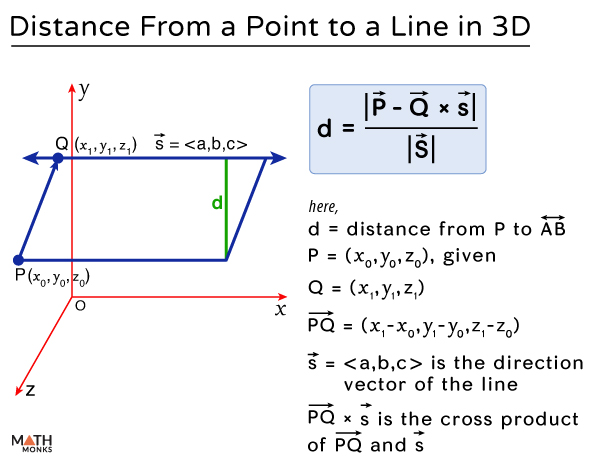
In a 3D Plane
If the point is P (x0, y0, z0) and the line ‘L’ in 3D has the equation ${\dfrac{x-x_{1}}{a}=\dfrac{y-y_{1}}{b}=\dfrac{z-z_{1}}{c}}$, then the distance ‘d’ from the point ‘P’ to the line ‘L’ is given by
${d=\dfrac{\left| \overrightarrow{PQ}\times \overrightarrow{s}\right| }{\left| \overrightarrow{s}\right| }}$
Here,
Q (x1, y1, z1) is a point on the line ‘L’
${\overrightarrow{PQ}}$ = the vector from the point P to Q with the coordinates (x1 – x0, y1 – y0, z1 – z0)
${\overrightarrow{s}}$ = ${\langle a,b,c\rangle}$ is the direction vector of the line
${\overrightarrow{PQ}\times \overrightarrow{s}}$ is the cross product of the vectors ${\overrightarrow{PQ}}$ and ${\overrightarrow{s}}$
Distance Between Two Lines
While calculating the distance between two lines in 2D and 3D spaces, we use the following formulas:
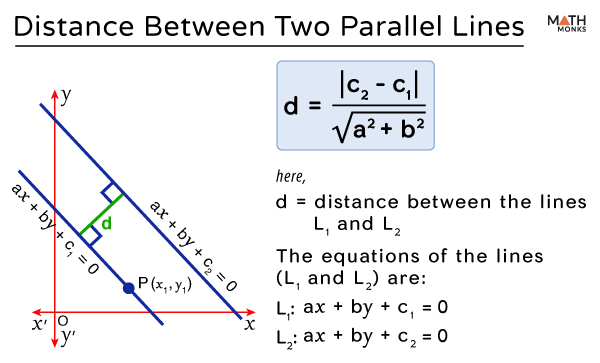
Two Parallel Lines in a 2D Plane
If we consider two lines L1: ax + by + c1 = 0 and L2: ax + by + c2 = 0, then the distance ‘d’ between the lines ‘L1’ and ‘L2’ is given by the formula:
${d=\dfrac{\left| c_{2}-c_{1}\right| }{\sqrt{a^{2}+b^{2}}}}$
Two Skewed Lines in a 3D Plane
Two lines are called skew lines in a three-dimensional plane if they are non-parallel and non-intersecting. Depending on whether they are in the cartesian or vector form, the shortest distance between them can be calculated using one of the following formulas.
In Cartesian Form
The distance between two lines given as L1: ${\dfrac{x-x_{1}}{a_{1}}=\dfrac{y-y_{1}}{b_{1}}=\dfrac{z-z_{1}}{c_{1}}}$ and L2: ${\dfrac{x-x_{2}}{a_{2}}=\dfrac{y-y_{2}}{b_{2}}=\dfrac{z-z_{2}}{c_{2}}}$ is: ${d=\left| \dfrac{\begin{vmatrix} x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\ a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{vmatrix}}{\left[ \left( b_{1}c_{2}-b_{2}c_{1}\right) ^{2}+\left( c_{1}a_{2}-a_{1}c_{2}\right) ^{2}+\left( a_{1}b_{2}-b_{1}a_{2}\right) ^{2} \right] ^\dfrac{1}{2}}\right|}$
In Vector Form
The distance between two lines given as L1: r1 = a1 + tb1 and L2: r2 = a2 + tb2 is: ${d=\dfrac{\left| \left( \overrightarrow{a}_{2}-\overrightarrow{a}_{1}\right) \cdot \left( \overrightarrow{b}_{1}\times \overrightarrow{b}_{2}\right) \right| }{\left| \overrightarrow{b}_{1}\times \overrightarrow{b}_{2}\right| }}$
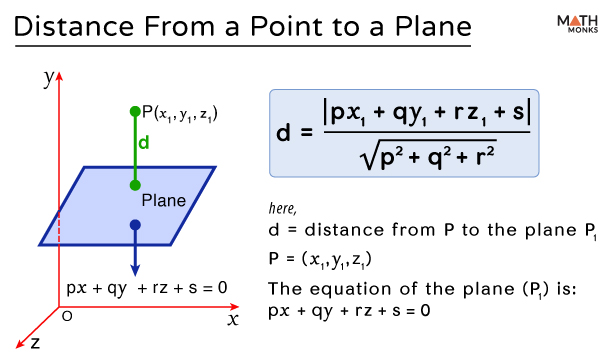
Distance from a Point to a Plane
The distance ‘d’ from a point P (x1, y1, z1) to a plane px + qy + rz + s = 0 is given by:
${d=\dfrac{\left| px_{1}+qy_{1}+rz_{1}+s\right| }{\sqrt{p^{2}+q^{2}+r^{2}}}}$
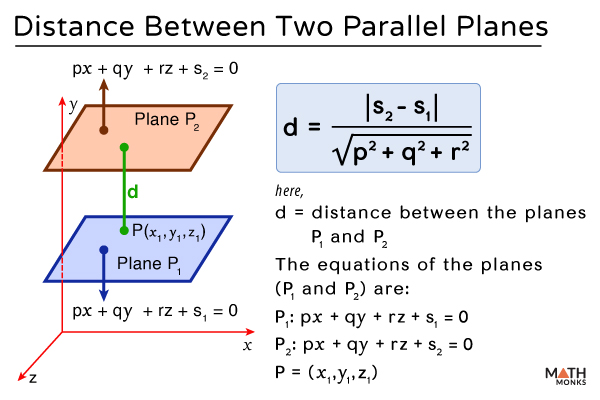
Distance between Two Parallel Planes
If the equations of two parallel planes are px + qy + rz + s1 = 0 and px + qy + rz + s2 = 0, then the distance ‘d’ between the two parallel planes is calculated by the formula:
${d=\dfrac{\left| s_{2}-s_{1}\right| }{\sqrt{p^{2}+q^{2}+r^{2}}}}$
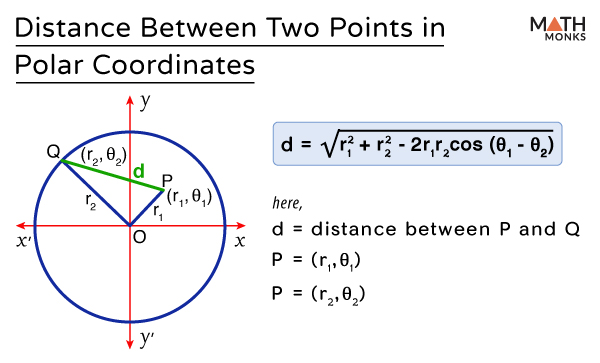
Distance between Two Points in Polar Coordinates
If ‘O’ is the pole and OX is the initial line, then for two given points P (r1, θ1) and Q (r2, θ2), the distance between two points formula is given by
${PQ=\sqrt{r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos \left( \theta _{1}-\theta _{2}\right) }}$
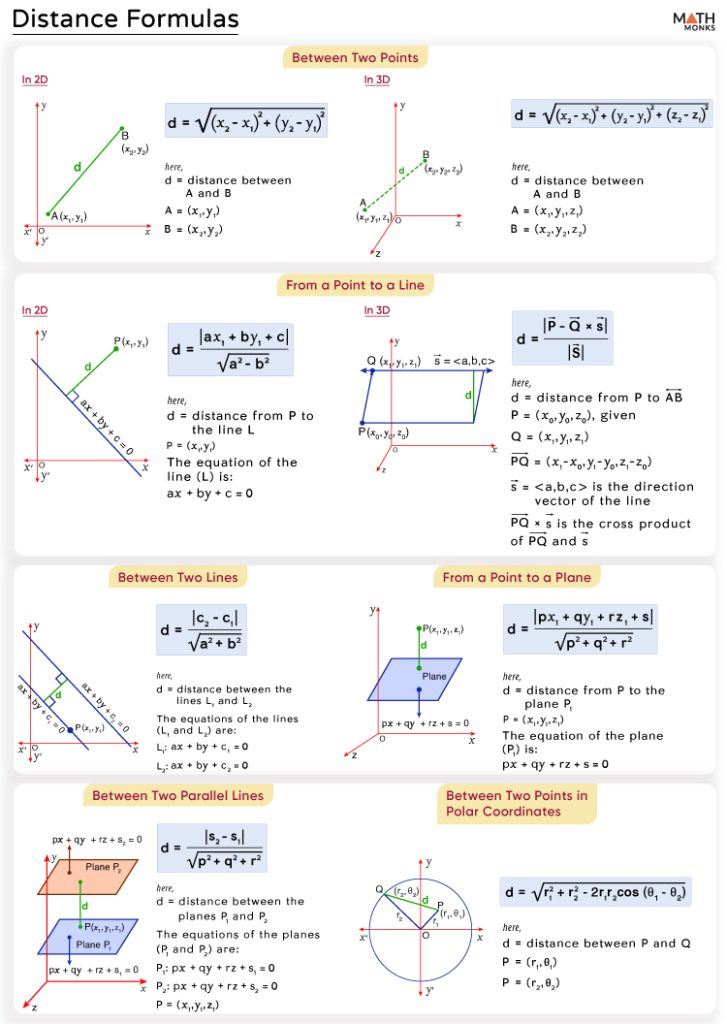
Here is the list of the different forms of the distance formula we learned:
………………………………………………………………..
Between Two Points in Polar Coordinates


 Find the distance between two points ‘A’ and ‘B’ in the given figure.
Find the distance between two points ‘A’ and ‘B’ in the given figure.