Equation of a Straight Line

The equation of a line is an expression that describes a straight line by defining the relationship between its points in a coordinate plane. Each point on the line is represented by a coordinate (x, y). There are an infinite number of points on a line.

It is thus a linear equation with a degree of 1. 

The equation of a line can be expressed in various forms depending on the given information. 

Standard Form

The standard or general form of the equation of a line:

For One Variable is Ax + B = 0

For Two Variable is Ax + By = C

Here, 

• A, B, and C are constants
• x and y are variables 

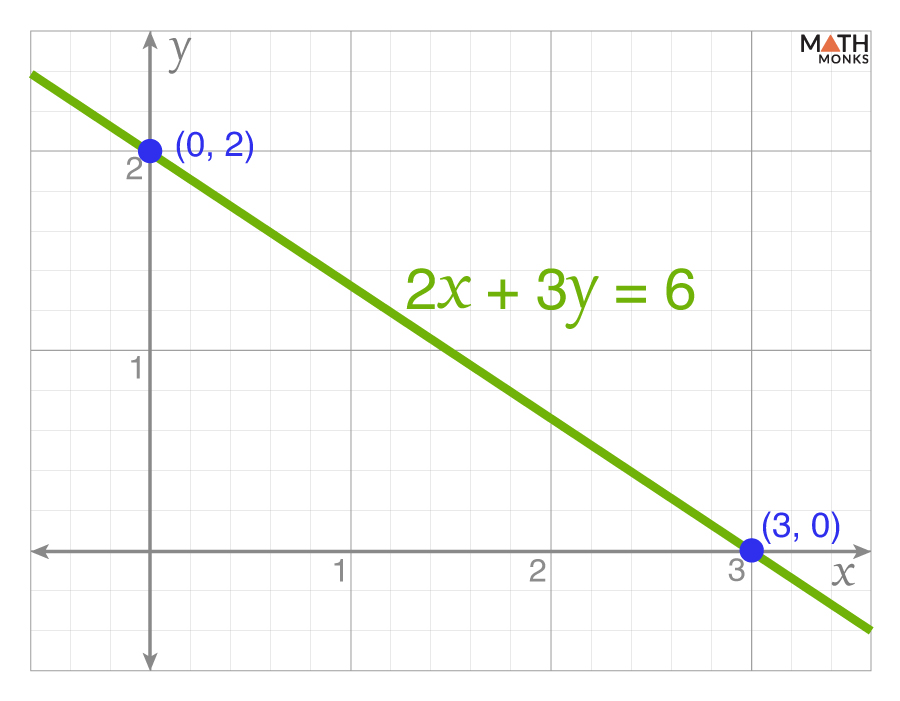
The equation 2x + 3y = 6 represents a line in standard form.

Slope-Intercept Form

The equation of a line is most commonly written in the slope-intercept form, which is written as:

y = mx + b (written as y = mx + c in UK)

Here,

• m is the slope of the line
• b is the y-intercept (where the line crosses the y-axis)

Thus, we need the slope and the y-intercept to find the equation of the line. 

The slope can be positive (the line goes up as you move to the right), negative (the line goes down as you move to the right), or zero (a horizontal line). The line is said to be undefined if it is vertical.

For example,

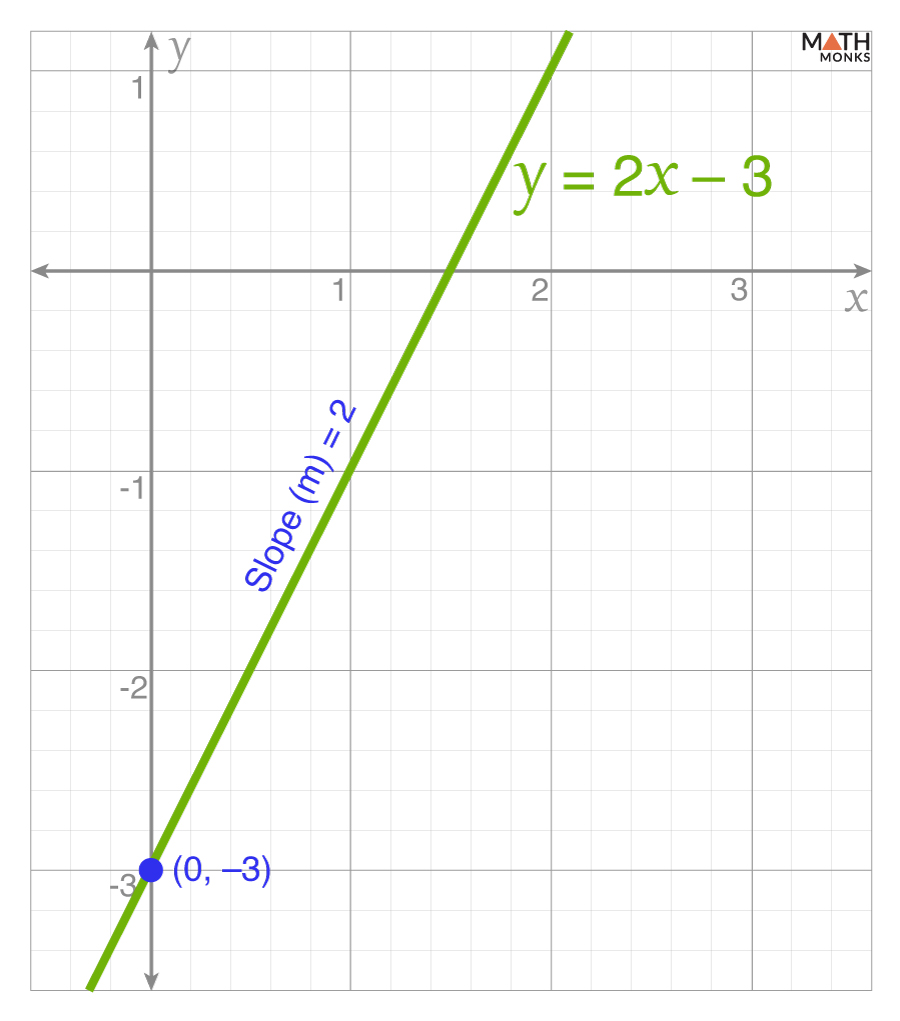
If a line has a slope of 2 and a y-intercept of -3, its equation is: y = 2x – 3. The equation has a positive slope.

Point-Slope Form

Given a point on the line and the slope, we use the point-slope form, which is written as:

y – y₁ = m(x – x₁)

Here,

• m is the slope of the line
• (x₁, y₁) is the coordinates of a point

For example,

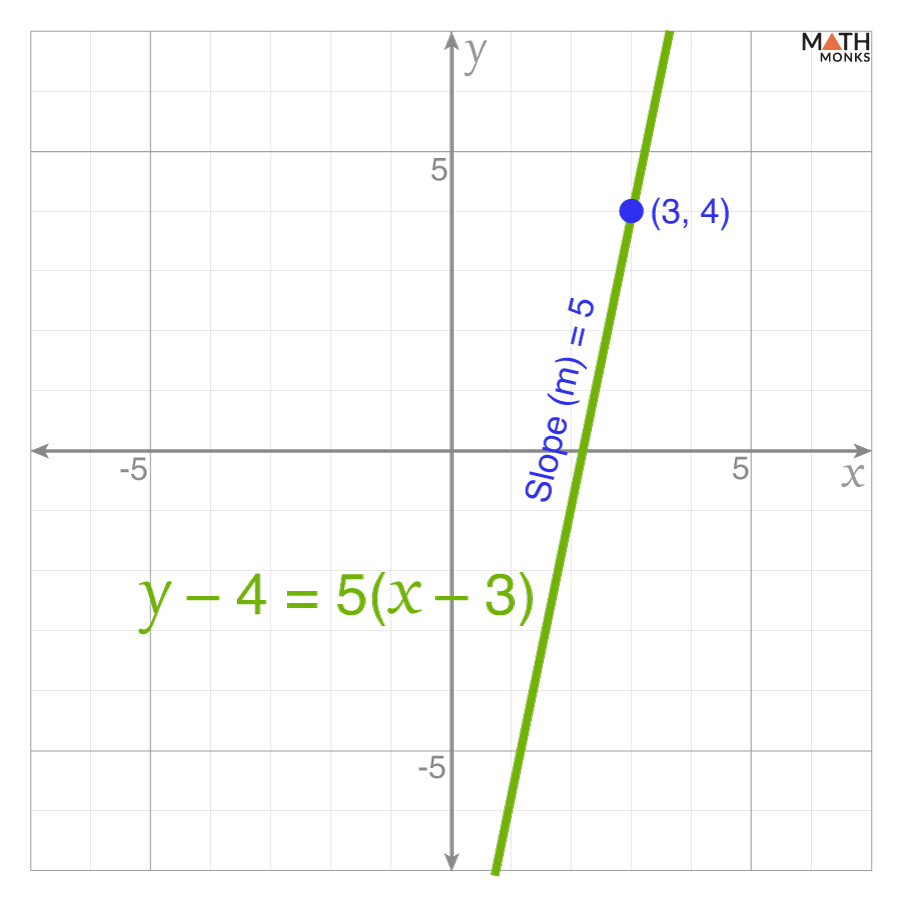
If a point is (3, 4) and a slope is 5, the equation of the line is: y – 4 = 5(x – 3)

Two-Point Form

When any two points of a line are known, say (x₁, y₁) and (x₂, y₂), we use the two-point form:

${\dfrac{y-y_{1}}{y_{2}-y_{1}}=\dfrac{x-x_{1}}{x_{2}-x_{1}}}$

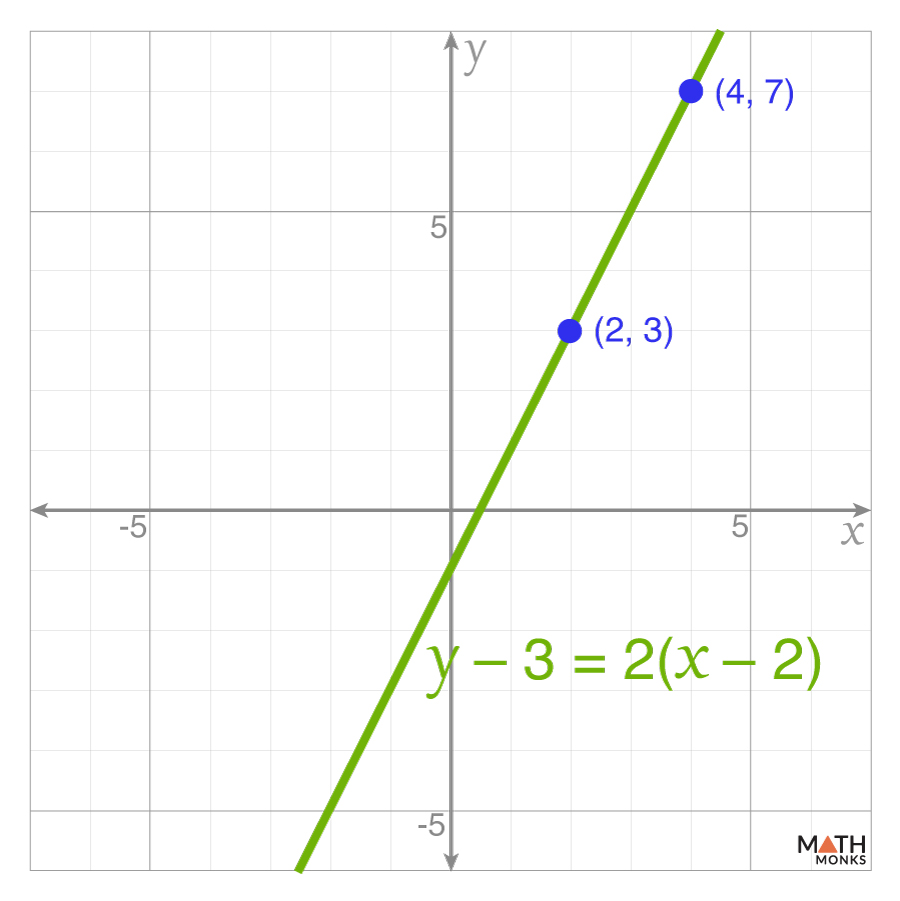
If (2, 3) and (4, 7) are two given points of a line, then the equation is:

${\dfrac{y-3}{7-3}=\dfrac{x-2}{4-2}}$, which simplifies to y – 3 = 2(x – 2)

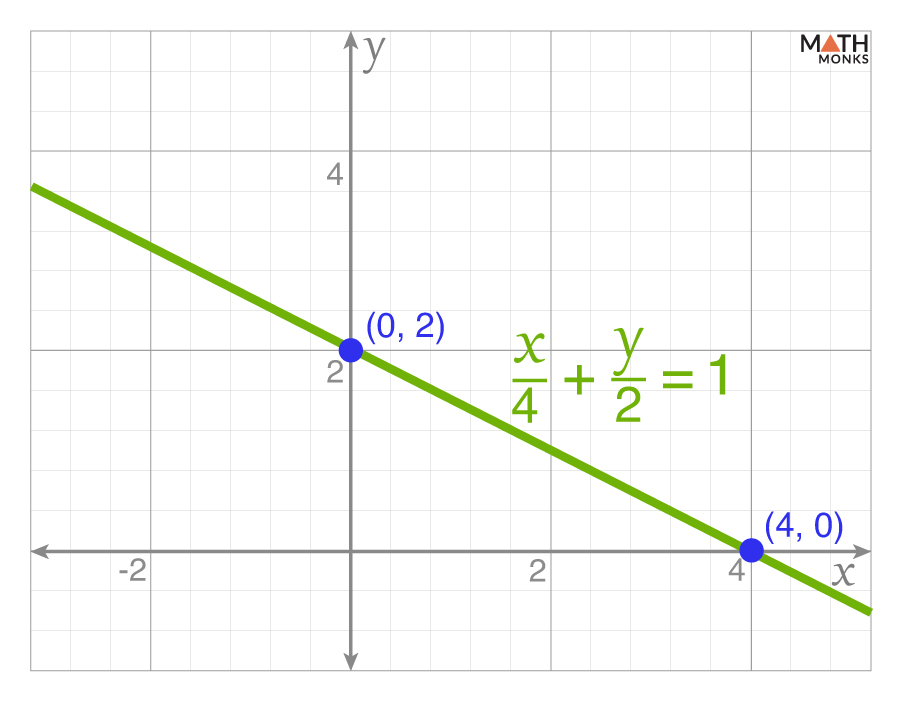
Intercept Form

If the line makes intercepts both at the x- and y-axis, say at a and b, respectively, we use the intercept form: 

${\dfrac{x}{a}+\dfrac{y}{b}=1}$

For example,

If a line crosses the x-axis at 4 and the y-axis at 2, the equation of the line is:

${\dfrac{x}{4}+\dfrac{y}{2}=1}$

Horizontal and Vertical Line

• y = b is the equation of a horizontal line, where b is the y-coordinate of any point on the line. 
• x = a is the equation of a vertical line, where a is the x-coordinate of any point on the given line. 

Summary

Below are the different ways we learned to express the equation of a straight line:

Solved Examples