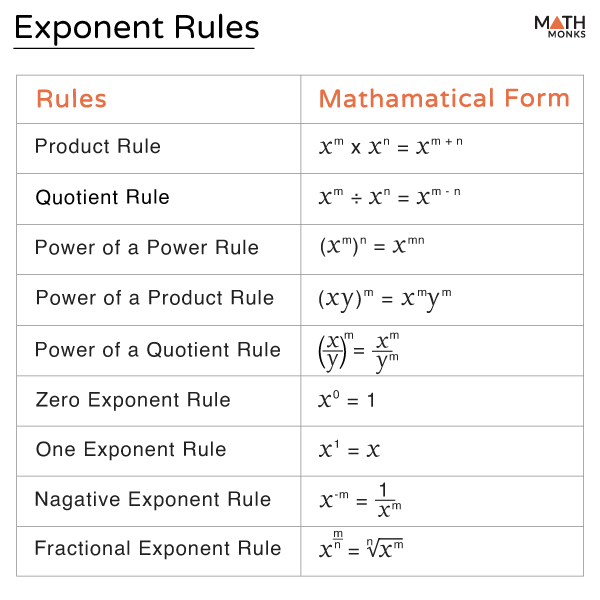
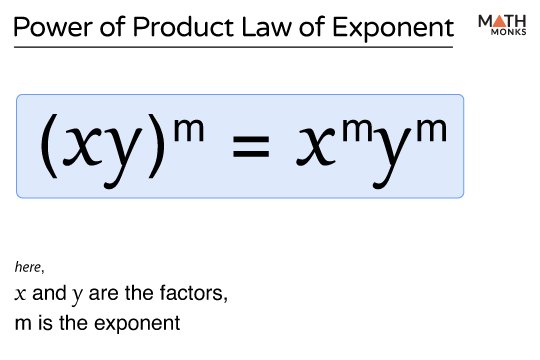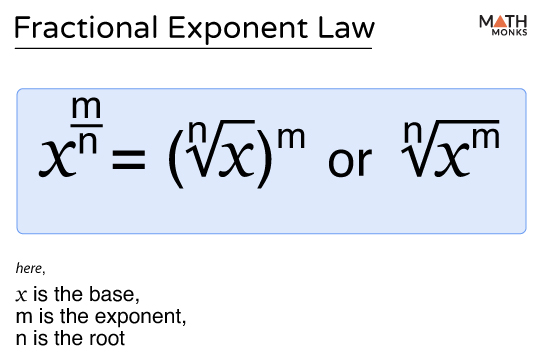Exponent Rules

Exponent rules, also known as ‘laws of exponents’ or ‘properties of exponents, ’ are certain rules that help us to simplify expressions involving exponents that can be decimal numbers, fractions, or irrational numbers.

Product Rule

It states that when we multiply two expressions with the same base, we add their exponents.

Mathematically, 

For example, if we multiply 8² and 8⁷ without using the product rule, we have a long calculation to do:

8² × 8⁷ = (8 × 8) × (8 × 8 × 8 × 8 × 8 × 8 × 8) = 8⁹

Instead, by using the product rule, we get

8² × 8⁷ = 8^{2 + 7} = 8⁹ 

This rule simplifies multiplying powers with the same base by adding the exponents into a single expression.

Quotient Rule

It states that when dividing two expressions with the same base, we subtract the exponent of the denominator from the exponent of the numerator.

Mathematically, 

For example,

${\dfrac{5^{6}}{5^{2}}=5^{6-2}}$ = ${5^{4}}$

This rule simplifies division by subtracting the exponents when the bases are the same. Without applying the rule, the calculation would be:

${\dfrac{5^{6}}{5^{2}}}$ = ${\dfrac{5\times 5\times 5\times 5\times 5\times 5}{5\times 5}}$ = ${5\times 5\times 5\times 5}$ = 5⁴ 

Power of a Power Rule

It states that when we raise an expression with an exponent to another exponent, we multiply the exponents together. 

Mathematically,

For example, if we multiply 8² and 8⁷ without using the law, the expression involves more calculations like this:

(7³)⁴ = (7 × 7 × 7) × (7 × 7 × 7) × (7 × 7 × 7) × (7 × 7 × 7) = 7¹²

Now, using the power rule, we get

(7³)⁴ = 7^{3 × 4} = 7¹² 

Power of a Product Rule

It states that when a product is raised to a power, the exponent is applied to each factor in the product. 

Mathematically,

This rule is useful when simplifying expressions with multiple terms inside parentheses raised to a power.

For example, simplifying (ab)⁴ using the rule, 

(ab)⁴ = a⁴b⁴

Now, without using the law, 

(ab)⁴ = (ab) × (ab) × (ab) × (ab) = (a × a × a × a) × (b × b × b × b) = a⁴b⁴, which involves more steps and calculations.

Power of a Quotient 

It states that when a quotient is raised to a power, the exponent can be applied to both the numerator and the denominator separately. 

Mathematically, 

This rule is used to simplify expressions with exponents when fractions are involved.

For example, 

${\dfrac{a^{2}}{b^{2}}=\left( \dfrac{a}{b}\right) ^{2}}$

However, without using the law, we get

${\dfrac{a^{2}}{b^{2}}}$ = ${\dfrac{a\times a}{b\times b}}$ = ${\left( \dfrac{a}{b}\right) \times \left( \dfrac{a}{b}\right)}$ = ${\left( \dfrac{a}{b}\right) ^{2}}$

Zero Exponent Rule

It states that any non-zero base raised to the power of 0 is equal to 1. 

Mathematically,

For example,

5⁰ = 1 or (-9)⁰ = 1, which shows that the rule holds for any non-zero base.

One Exponent Rule

It states that any non-zero number or variable raised to the power of 1 is equal to itself.

Mathematically, 

For example,

8¹ = 8 or b¹ = b, the value remains the same as the base.

Negative Exponent Rule

It states that a negative exponent represents the reciprocal of the base raised to the corresponding positive exponent. 

Mathematically,

For example,

${2^{-5}=\left( \dfrac{1}{2}\right) ^{5}}$

The negative exponent rule is used to simplify expressions with negative exponents by converting them into fractions.

Fractional Exponent Rule

It states that a base raised to a fractional exponent is equal to the square root of the base. Mathematically, 

For example,

${8^{\dfrac{2}{3}}}$ = ${\sqrt[3]{8^{2}}}$ = ${\sqrt[3]{64}}$ = 4

The fractional exponent rule is used to simplify expressions with fractional exponents by converting them into roots and powers. To better understand this, visit our Fractional Exponent article.

Solved Examples