Factorial Function

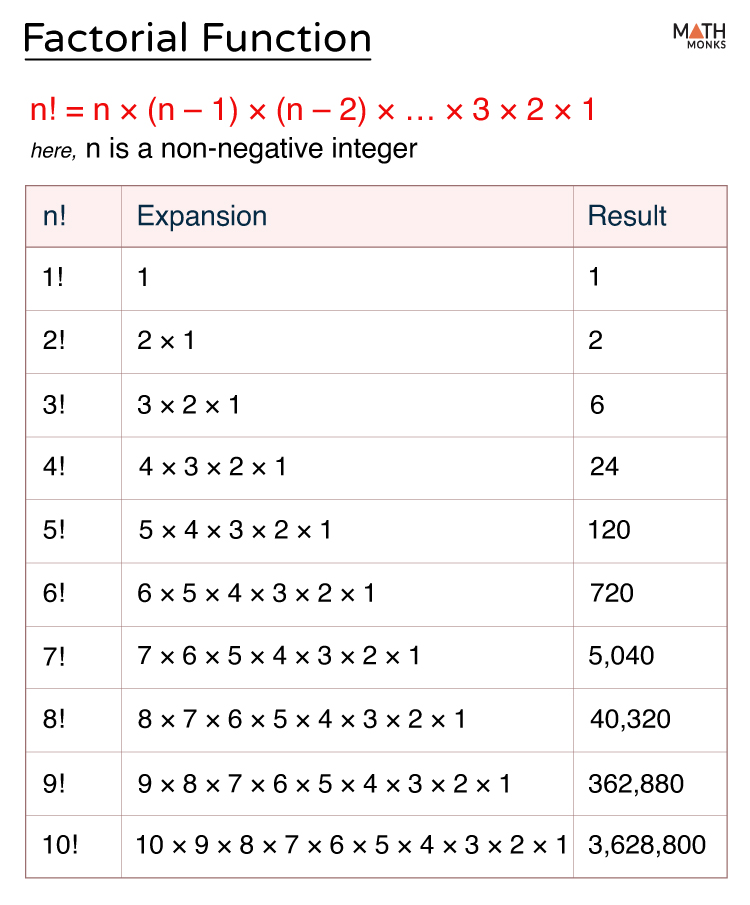
The factorial of a non-negative integer n, denoted by the symbol n! (read as ‘n factorial’), represents the product of all positive integers from 1 to n. 

n! = n × (n – 1) × (n – 2) × … × 3 × 2 × 1

Generally written as,

n! = n × (n – 1)!

Thus, the factorial value follows the recursive property, which means each factorial value builds upon the previous one. 

For example,

This pattern continues for larger values of n, and the factorial function grows faster than the exponential functions. 

Why is 0! = 1

At first, it may seem unusual that 0! = 1 since factorials involve multiplication. However, this can be explained using the backward pattern:

• 5! = 5 × 4 × 3 × 2 × 1 = 120
• 4! = 4 × 3 × 2 × 1 = 24
• 3! = 3 × 2 × 1 = 6
• 2! = 2 × 1 = 2
• 1! = 1

Thus, to maintain consistency, we define 0! = 1. 

Another explanation is obtained from combinatorics, where n! represents the number of ways to arrange n objects. When n = 0, there is exactly one way (doing nothing), so 0! = 1.

Extending Factorials to Decimals and Negative Numbers

Factorials are normally defined only for whole numbers, but they can be extended using the Gamma function.

Gamma Function (For Decimal Factorials)

For non-integer values, factorial is computed using the Gamma function (${\Gamma \left( n\right)}$):

${n!=\Gamma \left( n+1\right)}$

Here,

${\Gamma \left( n\right) =\int ^{\infty }_{0}x^{n-1}e^{-x}dx}$

For integer values, ${\Gamma \left( n+1\right) =n!}$. However, it also allows factorial-like computations for non-integer values.

For example, 

Let us find the factorial of 4.5

Here, by using the formula, we get

4.5! = ${\Gamma \left( 4.5+1\right)}$ = ${\Gamma \left( 5.5\right)}$ ≈ 52.34

For Negative Numbers

Factorials are not defined for negative integers because the Gamma function has singularities at negative integers.

For example, 

(-1)!, (-2)!, and (-5)! are all undefined.

Special Types

Half-Factorial (Semi-Factorial)

The half-factorial is the factorial of a half-integer (such as ${\dfrac{1}{2}}$, ${\dfrac{3}{2}}$, and ${\dfrac{5}{2}}$), and it is calculated using the Gamma function. These are used in probability and gamma distributions.

The formula for half factorial is:

${\left( \dfrac{1}{2}\right) !=\dfrac{1}{2}\sqrt{\pi }}$

The half-factorial follows the recursive property of factorials: (n + 1)! = (n + 1) × n!

For example,

${\left( \dfrac{3}{2}\right) !=\left( \dfrac{3}{2}\right) \times \left( \dfrac{1}{2}\right) !}$

Double Factorial (n!!)

The double factorial (n!!) is a variation of factorial where you multiply only every second number:

For even numbers: n!! = n × (n – 2) × (n – 4) × … × 2

For odd numbers: n!! = n × (n – 2) × (n – 4) × … × 1

For example,

6!! = 6 × 4 × 2 = 48

7!! = 7 × 5 × 3 × 1 = 105

Double factorials appear in combinatorics and physics calculations.

Subfactorial (!n)

The subfactorial (!n) represents the number of ways to rearrange n objects so that no object remains in its original place (called a ‘derangement’). These are used in probability and cryptography.

The formula of subfactorial is:

${!n=n!\sum ^{n}_{k=0}\dfrac{\left( -1\right) ^{k}}{k!}}$

A simpler approximation is: ${!n\approx \dfrac{n!}{e}}$

Factorial Arithmetic

Addition and Subtraction 

Factorials cannot be directly added or subtracted unless calculated separately.

For example,

5! + 3! = 120 + 6 = 126

6! – 4! = 720 – 24 = 696

Unlike regular numbers, factorials cannot be simplified algebraically in addition or subtraction.

Multiplication and Division 

Factorial properties allow simplifications in multiplication and division. These operations often involve simplifications using the factorial property n! = n × (n – 1)!

For example, 

3! × 4! = 6 × 24 = 144

${\dfrac{6!}{3!}}$ = ${\dfrac{720}{6}}$ = 120

Exponentiation

When raising factorials to a power, the exponent applies to the entire factorial. 

For example, (4!)² = (24)² = 576

Factorization

Sometimes, factorials appear in factorized forms in algebraic expressions. 

For example,

${\dfrac{\left( n+1\right) !}{n!}=\left( n+1\right)}$

Solved Examples