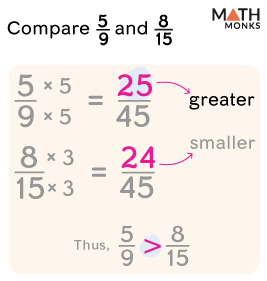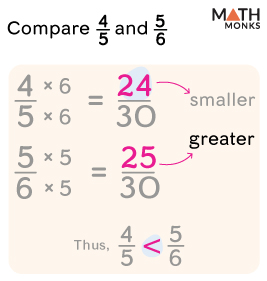We compare fractions to find which of the given fractions is greater, smaller, or equivalent.
With Same Denominators
When fractions have the same denominator, comparing them is easy. We just look at the numerator. The fraction with the larger numerator is the larger fraction.
Let us compare the fractions ${\dfrac{5}{7}}$ and ${\dfrac{2}{7}}$
Identifying the Denominators
Here, both denominators are 7
Comparing the Numerators
5 > 2
Thus, ${\dfrac{5}{7}}$ > ${\dfrac{2}{7}}$
With Different Denominators
When fractions have different denominators, we need to find a common denominator before comparing them. A common denominator is a shared multiple of the denominators of the given fractions.
Common Denominator Method
To compare the fractions with different denominators, we first convert them to like fractions by finding their LCM (Least Common Multiple).
Finding the LCD involves identifying the smallest number that both denominators share as a multiple. Next, we convert each fraction to an equivalent fraction with the LCD as the new denominator.
Let us compare the fractions ${\dfrac{1}{6}}$ and ${\dfrac{5}{9}}$
Finding the LCD
Here, the denominators are 6 and 9
The LCM of 6 and 9 is 18
Converting each Fraction to an Equivalent Fraction with LCD as the Denominator
${\dfrac{1}{6}}$ = ${\dfrac{1\times 3}{6\times 3}}$ = ${\dfrac{3}{18}}$
${\dfrac{5}{9}}$ = ${\dfrac{5\times 2}{9\times 2}}$ = ${\dfrac{10}{18}}$
Comparing the Numerators
10 > 3
Thus, ${\dfrac{10}{18}}$ > ${\dfrac{3}{18}}$
⇒ ${\dfrac{5}{9}}$ > ${\dfrac{1}{6}}$
![]() Compare ${\dfrac{4}{5}}$ and ${\dfrac{5}{6}}$
Compare ${\dfrac{4}{5}}$ and ${\dfrac{5}{6}}$
Solution:
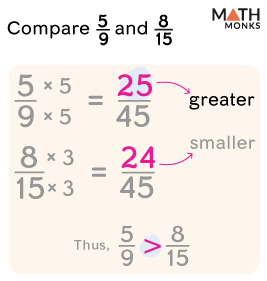
![]() Compare ${\dfrac{5}{9}}$ and ${\dfrac{8}{15}}$
Compare ${\dfrac{5}{9}}$ and ${\dfrac{8}{15}}$
Solution:
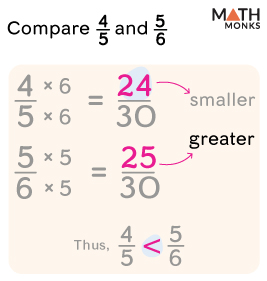
Using the Decimal Values
Here, we convert each fraction to its equivalent decimal values and then compare the decimal values.
Let us compare between ${\dfrac{2}{5}}$ and ${\dfrac{3}{8}}$
Dividing the Numerators by the Denominators
${\dfrac{2}{5}}$ = 0.4
${\dfrac{3}{8}}$ = 0.375
Comparing the Decimal Values
0.4 > 0.375
Thus, ${\dfrac{2}{5}}$ > ${\dfrac{3}{8}}$
Using Cross Multiplication
Another method to compare fractions with different denominators is cross-multiplication. This method eliminates the need to find a common denominator.
Here, we multiply the numerator of one fraction with the denominator of the other and vice versa. The fraction with the larger product is the larger fraction. It is also known as the butterfly method.
If we compare ${\dfrac{4}{9}}$ and ${\dfrac{2}{7}}$
Cross-Multiplying and Comparing the Product
Thus, ${\dfrac{4}{9}}$ > ${\dfrac{2}{7}}$
Visually
We use various graphical models to visualize fractions, which helps us to compare them.
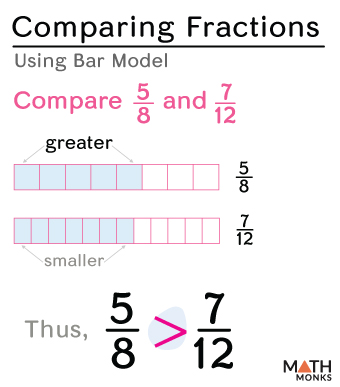
Using Bar-Model
Comparing both fractions ${\dfrac{5}{8}}$ and ${\dfrac{7}{12}}$ by their shaded region gives us the greater or smaller fraction.
${\dfrac{5}{8}}$ > ${\dfrac{7}{12}}$ as ${\dfrac{5}{8}}$ covers a larger shaded area of the same whole than ${\dfrac{7}{12}}$.
Using Number Line
We can also compare fractions on a number line. Here, we first convert them into like fractions and then plot them on the number line.
Let us compare between ${\dfrac{5}{8}}$ and ${\dfrac{7}{12}}$
Problem – Comparing Fractions Using BENCHMARKS
![]() Compare ${\dfrac{5}{6}}$ and ${\dfrac{1}{3}}$
Compare ${\dfrac{5}{6}}$ and ${\dfrac{1}{3}}$
Solution:
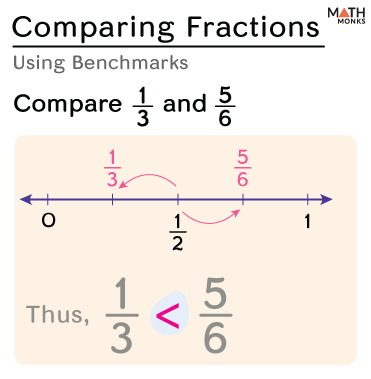
We can also compare fractions on a number line by using the benchmark fractions 0, ${\dfrac{1}{2}}$ and 1
Let us compare ${\dfrac{5}{6}}$ and ${\dfrac{1}{3}}$
On plotting them on a number line, we get
The fraction ${\dfrac{5}{6}}$ is more than ${\dfrac{1}{2}}$, while ${\dfrac{1}{3}}$ is less than ${\dfrac{1}{2}}$
Thus, ${\dfrac{1}{3}}$ < ${\dfrac{5}{6}}$
With Same Numerators
To compare fractions with the same numerators, we compare them by their denominators. The fraction with the greatest denominator is the smallest, and vice versa.
Let us compare ${\dfrac{3}{8}}$ and ${\dfrac{3}{14}}$
Identifying the Numerators
Here, both the numerators are 3
Comparing the Denominators
8 < 14
Thus, ${\dfrac{3}{14}}$ < ${\dfrac{3}{8}}$