Cross Multiplying with Fractions

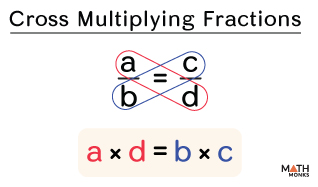
To cross-multiply fractions, we multiply the numerator of the first fraction by the denominator of the second fraction and vice versa.

In the algebraic equation ${\dfrac{a}{b}=\dfrac{c}{d}}$, the cross multiplication is given by the formula ${a\times d=b\times c}$

Cross multiplication is used to compare fractions, add or subtract unlike fractions, find an unknown value in an expression, and compare ratios.

For example,

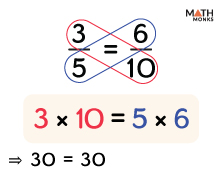
Thus, by cross-multiplying ${\dfrac{3}{5}=\dfrac{6}{10}}$, we get ${3\times 10=5\times 6}$ (which implies 30 = 30)

Cross-multiplication is also used to solve the value of the unknown variables in any equation. 

With One Variable

If we have one variable on each side, we solve the equation in the following way.

Let us solve ${\dfrac{6}{5}=\dfrac{x}{20}}$ for x

Cross-Multiplying

${6\times 20=5\times x}$

⇒ ${120=5x}$

Dividing both sides by 5

⇒ ${\dfrac{5x}{5}=\dfrac{120}{5}}$

⇒ ${x=24}$

Thus, the solution is x = 24

With Two Variables

If the same variable is present on both sides of the equation, then we cross-multiply to find the variable.

Let us solve ${\dfrac{x}{9}=\dfrac{4}{x}}$ for x

Cross-Multiplying

${x\times x=9\times 4}$

⇒ ${x^{2}=36}$

Finding Square Roots of Both Sides

⇒ ${x=\sqrt{36}}$

⇒ ${x=6}$

Thus, the solution is x = 6

Comparing

Unlike Fractions

To compare unlike fractions, we convert their denominators to a common value by multiplying the two original denominators together, ensuring both fractions have the same denominator.

For example, 

Let us compare ${\dfrac{3}{8}}$ and ${\dfrac{4}{5}}$ by cross multiplication.

Here, the denominators are 8 and 5

Thus, the denominators of both fractions become ${8\times 5=40}$

Now, cross -multiplying to get the numerators,

${3\times 5=15}$ and ${8\times 4=32}$

Thus, the fractions become ${\dfrac{15}{40}}$ and ${\dfrac{32}{40}}$

Now, comparing the fractions,

${\dfrac{15}{40}}$ < ${\dfrac{32}{40}}$

⇒ ${\dfrac{3}{8}}$ < ${\dfrac{4}{5}}$

When the resulting fractions are the same, they are equivalent fractions. 

Ratios

If two ratios are equal (where b, d ≠ 0), then the cross-multiplication product is also equal. 

On comparing the ratios: 

• ${\dfrac{a}{b}=\dfrac{c}{d}}$, if ${a\times d=b\times c}$
• ${\dfrac{a}{b}<\dfrac{c}{d}}$, if ${a\times d<b\times c}$
• ${\dfrac{a}{b}>\dfrac{c}{d}}$, if ${a\times d>b\times c}$

Now, let us compare 2:4 and 5:10

Here, the fractions are ${\dfrac{2}{4}}$ and ${\dfrac{5}{10}}$

${2\times 10=20}$ and ${4\times 5=20}$

Since ${2\times 4=5\times 10}$

Thus, the ratios 2:4 and 5:10 are equivalent.