‘Decomposing’ a fraction means breaking it into partial fractions. Adding all these smaller parts gives back the original fraction.
Decomposition allows us to visualize the fraction in different parts, which can be useful in various mathematical operations such as addition and subtraction. They also help in understanding mixed numbers.
How to Decompose
It is done in two ways: decomposing into unit fractions and non-unit fractions.
Into Unit Fractions
When we break a fraction into unit fractions, we split it into equal parts, and each part represents one part of the whole. It involves two steps: 1) identifying the fraction and 2) Breaking it down into unit fractions.
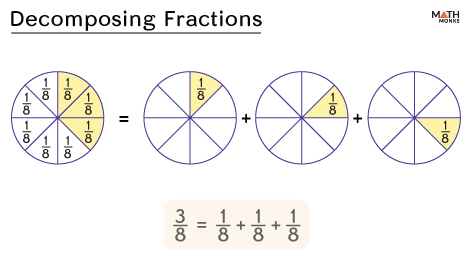
Let us decompose the fraction ${\dfrac{3}{8}}$. It represents 3 out of 8 equal parts.
The fraction ${\dfrac{3}{8}}$ is decomposed into three one-eighths. On adding these parts together, we get the fraction ${\dfrac{3}{8}}$, as shown.
${\dfrac{3}{8}}$ = ${\dfrac{1}{8}+\dfrac{1}{8}+\dfrac{1}{8}}$
This is the most common way of decomposing fractions.
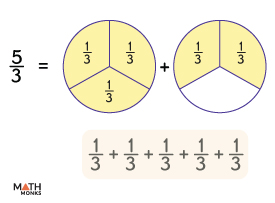
Let us now decompose ${\dfrac{5}{3}}$
${\dfrac{5}{3}}$ is the same as seven times the unit fraction ${\dfrac{1}{3}}$, so it is divided as follows:
${\dfrac{5}{3}}$ = ${\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}}$
Into Non-Unit Fractions
Unlike breaking into an equal number of units fractions, we can also decompose a fraction into non-equal parts. These parts are non-unit fractions.
Similar to adding unit fractions, if we add up the non-unit fractions, we will get back the same original fraction.
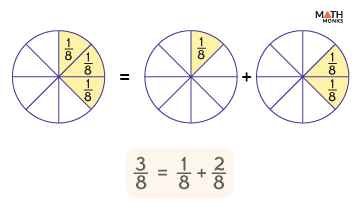
Let us decompose ${\dfrac{3}{8}}$ into non-unit fractions
Here, the circle, which is considered as a whole, is divided into two unequal parts.
${\dfrac{3}{8}}$ = ${\dfrac{1}{8}+\dfrac{2}{8}}$
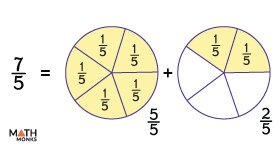
Now, let us now decompose ${\dfrac{7}{5}}$.
Here, the fraction is divided into two parts, as shown
${\dfrac{7}{5}}$ = ${\dfrac{5}{5}+\dfrac{2}{5}}$ = ${1+\dfrac{2}{5}}$
This gives the mixed number in the form of ${1\dfrac{2}{5}}$
For Mixed Numbers
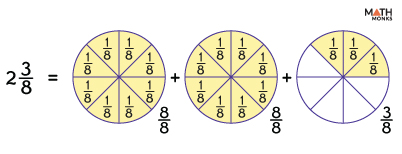
Let us decompose a mixed number ${2\dfrac{3}{8}}$ that is between the whole numbers 2 and 3.
As shown, the mixed number is divided into the following three non-unit fractions.
${2\dfrac{3}{8}}$ = ${\dfrac{8}{8}+\dfrac{8}{8}+\dfrac{3}{8}}$
Solved Examples
![]() Decompose ${\dfrac{5}{6}}$ into three fractions.
Decompose ${\dfrac{5}{6}}$ into three fractions.
Solution:
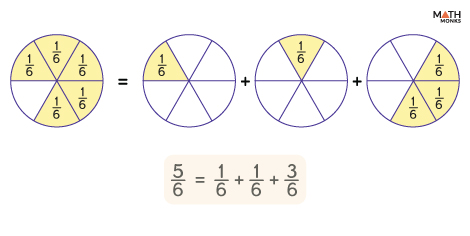
Given, ${\dfrac{5}{6}}$
This is the same as five times one-sixth
Decomposing the given fraction,
${\dfrac{5}{6}}$ = ${\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{3}{6}}$
![]() Decompose ${\dfrac{3}{4}}$ into a sum of unit fractions.
Decompose ${\dfrac{3}{4}}$ into a sum of unit fractions.
Solution:
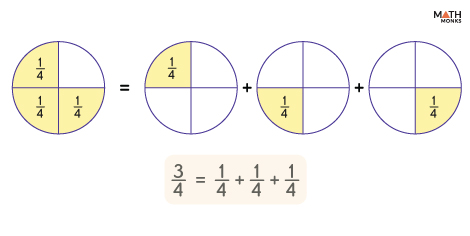
Given, ${\dfrac{3}{4}}$
This is the same as seven times one-eighths
Decomposing the given fraction
${\dfrac{3}{4}}$ = ${\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{4}}$