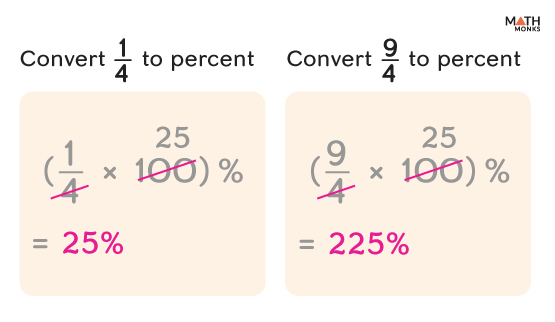Fraction to Percent

To convert a fraction to a percent, we first convert it to decimal, multiply it by 100 to get the percentage value, and finally add a ‘%’ sign.

It helps us to compare and order two quantities more easily. 

Let us convert ${\dfrac{1}{4}}$ to percent.

Dividing the Numerator by the Denominator of the Fraction 

${\dfrac{1}{4}}$ = 0.25

Multiplying the Result by 100 and Moving the Decimal Point to the Right 

0.25 × 100 = 25%

Here, the answer is less than 100% as  ${\dfrac{1}{4}}$ is a proper fraction.

Formula

Thus, the formula to convert fraction ${\dfrac{p}{q}}$ to percentage is:

${\dfrac{p}{q}}$ = ${\left( \dfrac{p}{q}\times 100\right)}$ %

Here, 

p = Numerator

q = Denominator

This is another way of converting a fraction to a percent where we multiply the fraction by 100, simplify it, and then add a ‘%’ sign. 

For example, 

${\dfrac{1}{4}}$ = ${\dfrac{1}{4}\times 100}$ = 25%

Alternative Method

In this method,  we find the equivalent fraction with a denominator of 100. Then, the numerator with the ‘%’ sign represents the percent.

Let us convert ${\dfrac{1}{4}}$ into percent.

Multiplying the Denominator by a Number to get 100 

Since 4 × 25 = 100

Thus, we multiply 25 by the denominator 4 to get 100

Multiplying the Numerator by the Same Number 

${\dfrac{1\times 25}{4\times 25}}$ = ${\dfrac{25}{100}}$

Writing the Numerator with the ‘%’ Sign 

Thus, the percentage is 25%

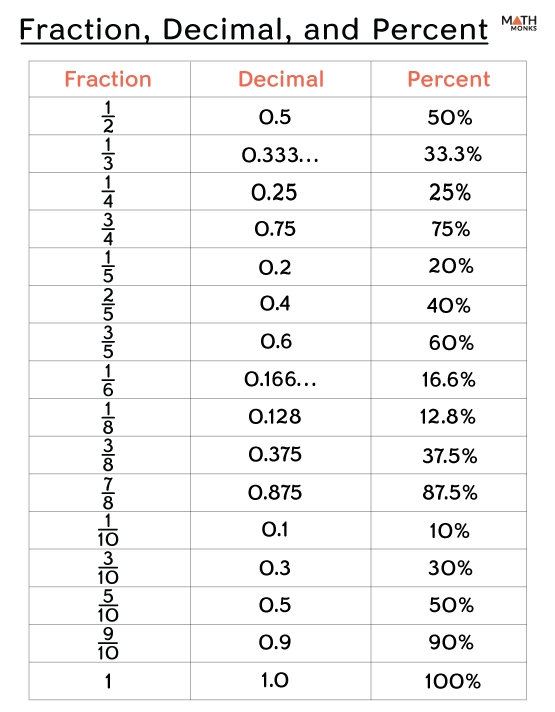
Fraction to Percent Table

Here is a fractions-to-percent conversion table for your use.

For Improper Fractions

While converting an improper fraction to a percent, we follow the same steps.

Let us convert ${\dfrac{9}{4}}$ to percent.

Converting to Decimal Number

${\dfrac{9}{4}}$ = 2.25

Multiplying the Decimal Number by 100 

2.25 × 100 = 225%

Here, we observe that the answer is above 100%, as ${\dfrac{9}{4}}$ is an improper fraction.

Solved Examples