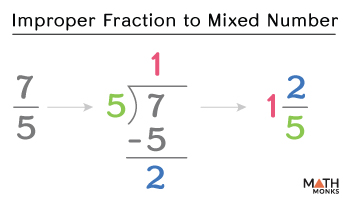Improper fractions are converted to mixed numbers to make them easier to understand and visualize. It also helps simplify comparisons and calculations and provides a clearer representation of the value.
It is important to note that an improper fraction and its corresponding mixed number have the same value. They are only represented differently.
How To Convert
To convert an improper fraction ${\dfrac{7}{5}}$ to a mixed number, we follow the following steps.
Step 1: Dividing the Numerator by the Denominator
7 ÷ 5
The quotient = 1 and the remainder = 2.
Step 2: Writing in the Form ${Quotient\dfrac{Remainder}{Divisor}}$
The mixed number obtained is ${1\dfrac{2}{5}}$
Let us consider another example.
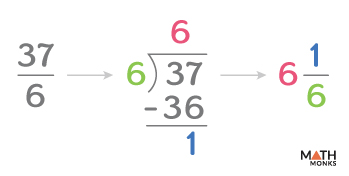
To convert ${\dfrac{37}{6}}$ into a mixed number, we divide 37 by 6
37 ÷ 6
The quotient = 6 and the remainder = 1
Thus, the improper fraction ${\dfrac{37}{6}}$ as a mixed number is ${6\dfrac{1}{6}}$
Adding Improper Fraction to Mixed Number
Let us add ${\dfrac{8}{3}}$ and ${1\dfrac{3}{4}}$
Converting the Mixed Number to an Improper Fraction
${1\dfrac{3}{4}}$ = ${\dfrac{\left( 1\times 4\right) +3}{4}}$ = ${\dfrac{7}{4}}$
Adding
Now, ${\dfrac{8}{3}+1\dfrac{3}{4}}$
= ${\dfrac{8}{3}+\dfrac{7}{4}}$
= ${\dfrac{8\times 4}{3\times 4}+\dfrac{7\times 3}{4\times 3}}$
= ${\dfrac{32}{12}+\dfrac{21}{12}}$
= ${\dfrac{32+21}{12}}$
= ${\dfrac{53}{12}}$
Converting the Result to a Mixed Number
= ${4\dfrac{5}{12}}$
Thus, the sum is ${4\dfrac{5}{12}}$
Solved Examples
![]() Convert the improper fraction ${\dfrac{8}{3}}$ to mixed number.
Convert the improper fraction ${\dfrac{8}{3}}$ to mixed number.
Solution:
![]()
Here,
The numerator = 8
The denominator = 3
8 ÷ 3
The quotient = 2 and the remainder = 2
Thus, the improper fraction ${\dfrac{8}{3}}$ as a mixed number is ${2\dfrac{2}{3}}$
![]() E.g.2. Change the improper fraction ${\dfrac{9}{4}}$ to mixed number.
E.g.2. Change the improper fraction ${\dfrac{9}{4}}$ to mixed number.
Solution:
![]()
Here,
The numerator = 9
The denominator = 4
9 ÷ 4
The quotient = 2 and the remainder = 1
Thus, the improper fraction ${\dfrac{9}{4}}$ as a mixed number is ${2\dfrac{1}{4}}$
![]() Turn the improper fraction ${\dfrac{62}{13}}$ into mixed number.
Turn the improper fraction ${\dfrac{62}{13}}$ into mixed number.
Solution:
![]()
Here,
The numerator = 62
The denominator = 13
62 ÷ 13
The quotient = 4 and the remainder = 10
Thus, the mixed number is ${4\dfrac{10}{13}}$
E.g.4.
![]() Write the improper fraction ${\dfrac{18}{7}}$ as mixed number.
Write the improper fraction ${\dfrac{18}{7}}$ as mixed number.
Solution:
![]()
Here,
The numerator = 18
The denominator = 7
18 ÷ 7
The quotient = 2 and the remainder = 4
Thus, the mixed number is ${2\dfrac{4}{7}}$
![]() Add the improper fraction and the mixed number:
Add the improper fraction and the mixed number:
${\dfrac{7}{5}}$ and ${1\dfrac{2}{3}}$
Solution:
![]()
Here,
${1\dfrac{2}{3}}$ = ${\dfrac{\left( 1\times 3\right) +2}{3}}$ = ${\dfrac{5}{3}}$
Now, ${\dfrac{7}{5}+1\dfrac{2}{3}}$
= ${\dfrac{7}{5}+\dfrac{5}{3}}$
= ${\dfrac{7\times 3}{5\times 3}+\dfrac{5\times 5}{3\times 5}}$
= ${\dfrac{21}{15}+\dfrac{25}{15}}$
= ${\dfrac{21+25}{15}}$
= ${\dfrac{46}{15}}$
= ${3\dfrac{1}{15}}$
Thus, the sum is ${3\dfrac{1}{15}}$