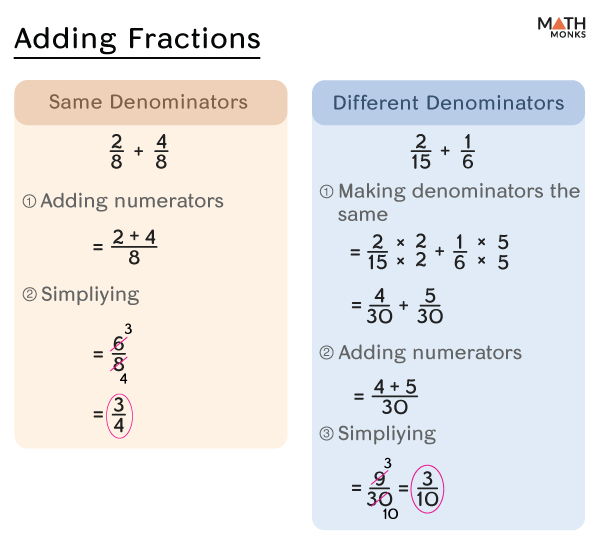
Adding fractions involves three basic steps:
- Identifying whether the denominators are the same. If they are the same, we move on to the next step. If they are different, we find their common denominators.
- Adding the numerators
- Simplifying the sum if needed.
With Like Denominators
To add fractions with like denominators, we just add the numerators and then write the sum over the common denominator.
Let us add the fractions ${\dfrac{2}{7}+\dfrac{4}{7}}$
Identifying the Denominators
Here, the denominators are 7
Adding the Numerators
${\dfrac{2+4}{7}}$
= ${\dfrac{6}{7}}$, which cannot be simplified or reduced further.
Thus, the sum is ${\dfrac{6}{7}}$
With Unlike Denominators
Let us add the unlike fractions ${\dfrac{2}{15}+\dfrac{1}{6}}$
Identifying the Denominators
Here, the denominators are 15 and 6, that are different.
Finding the LCM of the Denominators
The LCM of 15 and 6 is 30
Making the Denominators the Same
Converting ${\dfrac{2}{15}}$ and ${\dfrac{1}{6}}$ to their equivalent fractions with 30 as the denominator,
${\dfrac{2\times 2}{15\times 2}}$ = ${\dfrac{4}{30}}$
${\dfrac{1\times 5}{6\times 5}}$ = ${\dfrac{5}{30}}$
Now, we have ${\dfrac{4}{30}+\dfrac{5}{30}}$
Adding the Numerators
On adding the numerators,
${\dfrac{4+5}{30}}$
= ${\dfrac{9}{30}}$
Simplifying
${\dfrac{9\div 3}{30\div 3}}$
= ${\dfrac{3}{10}}$
Thus, the sum is ${\dfrac{3}{10}}$
![]() Add: ${\dfrac{7}{9}}$ and ${\dfrac{11}{3}}$
Add: ${\dfrac{7}{9}}$ and ${\dfrac{11}{3}}$
Solution:
![]()
Here, the denominators are 9 and 3
The LCM of 9 and 3 is 9
Now, ${\dfrac{7}{9}+\dfrac{11}{3}}$
= ${\dfrac{7}{9}+\dfrac{11\times 3}{3\times 3}}$
= ${\dfrac{7}{9}+\dfrac{33}{9}}$
= ${\dfrac{7+33}{9}}$
= ${\dfrac{40}{9}}$
= ${4\dfrac{4}{9}}$
Thus, the sum is ${4\dfrac{4}{9}}$
Problem: Adding a NEGATIVE FRACTION
![]() Add: ${\dfrac{5}{12}+\left( \dfrac{-1}{6}\right)}$
Add: ${\dfrac{5}{12}+\left( \dfrac{-1}{6}\right)}$
Solution:
![]()
Here, the denominators are 12 and 6
The LCM of 12 and 6 are 12
Now, ${\dfrac{5}{12}+\left( \dfrac{-1}{6}\right)}$
= ${\dfrac{5}{12}+\left( \dfrac{-1\times 2}{6\times 2}\right)}$
= ${\dfrac{5}{12}+\left( \dfrac{-2}{12}\right)}$
= ${\dfrac{5-2}{12}}$
= ${\dfrac{3}{12}}$
= ${\dfrac{1}{4}}$
Thus, the sum is ${\dfrac{1}{4}}$
With Co-Prime Denominators
Co-prime denominators are the denominators with no common factors between them other than 1.
Given, ${\dfrac{2}{7}+\dfrac{1}{5}}$
Identifying the Denominators
First, we identify the denominators and determine whether they are co-prime.
Here, the denominators are 7 and 5, that are co-prime.
Multiplying the First Fraction By the Denominator of the Second Fraction and Vice-Versa
${\dfrac{2\times 5}{7\times 5}+\dfrac{1\times 7}{5\times 7}}$
= ${\dfrac{10}{35}+\dfrac{7}{35}}$
Adding the Numerators
${\dfrac{10+7}{35}}$
= ${\dfrac{17}{35}}$
Thus, the sum is ${\dfrac{17}{35}}$
With Whole Numbers
Let us add: ${5+\dfrac{3}{8}}$
Converting the Whole Number to Fraction
${5}$ = ${\dfrac{5}{1}}$
Now, we have ${\dfrac{5}{1}+\dfrac{3}{8}}$
Identifying the Denominators
The denominators are 1 and 8, which are different.
Finding the LCM of the Denominators
The LCM of 1 and 8 is 8
Adding the Numerators
${\dfrac{5\times 8}{1\times 8}+\dfrac{3\times 1}{8\times 1}}$
= ${\dfrac{40}{8}+\dfrac{3}{8}}$
= ${\dfrac{40+3}{8}}$
= ${\dfrac{43}{8}}$
= ${5\dfrac{3}{8}}$
However, a simple way to add a whole number to a proper fraction is to combine and express them as a mixed number.
For example, ${5+\dfrac{3}{8}}$ is written as ${5\dfrac{3}{8}}$
With Mixed Numbers
To add fractions with mixed numbers, we convert the mixed numbers into improper fractions and then add them.
If ${\dfrac{5}{8}+1\dfrac{3}{10}}$
Converting to Improper Fraction
Converting ${1\dfrac{3}{10}}$ to improper fraction,
${1\dfrac{3}{10}}$ = ${\dfrac{\left( 1\times 10\right) +3}{10}}$ = ${\dfrac{13}{10}}$
Identifying the Denominators
Here, the denominators are 8 and 10
Finding the LCM of the Denominators
The LCM of 8 and 10 is 40
Making the Denominators the Same and Adding the Numerators
${\dfrac{5\times 5}{8\times 5}+\dfrac{13\times 4}{10\times 4}}$
= ${\dfrac{25}{40}+\dfrac{52}{40}}$
= ${\dfrac{25+52}{40}}$
= ${\dfrac{77}{40}}$
= ${1\dfrac{37}{40}}$
Thus, the sum is ${1\dfrac{37}{40}}$
![]() Find the sum of ${2\dfrac{1}{4}+\dfrac{1}{5}}$
Find the sum of ${2\dfrac{1}{4}+\dfrac{1}{5}}$
Solution:
![]()
Here, the denominators are 4 and 5
The LCM of 4 and 5 is 20
Also, ${2\dfrac{1}{4}}$ = ${\dfrac{\left( 2\times 4\right) +1}{4}}$ = ${\dfrac{9}{4}}$
Now, ${2\dfrac{1}{4}+\dfrac{1}{5}}$
= ${\dfrac{9}{4}+\dfrac{1}{5}}$
= ${\dfrac{9\times 5}{4\times 5}+\dfrac{1\times 4}{5\times 4}}$
= ${\dfrac{45}{20}+\dfrac{4}{20}}$
= ${\dfrac{45+4}{20}}$
= ${\dfrac{49}{20}}$
= ${2\dfrac{9}{20}}$
Thus, the sum is ${2\dfrac{9}{20}}$
With Variables
Now, let us add fractions, including variables.
If ${\dfrac{p}{2}+\dfrac{2p}{5}}$
Identifying the Denominators
The denominators are 2 and 5
Finding the LCM of the Denominators
The LCM of 2 and 5 is 10
Making the Denominators the Same and Adding the Numerators
${\dfrac{p\times 5}{2\times 5}+\dfrac{2p\times 2}{5\times 2}}$
= ${\dfrac{5p}{10}+\dfrac{4p}{10}}$
= ${\dfrac{5p+4p}{10}}$
= ${\dfrac{9p}{10}}$
Thus, the sum is ${\dfrac{9p}{10}}$