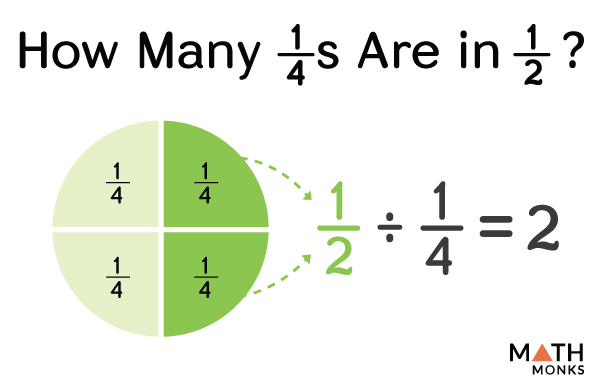Dividing Fractions

Like multiplication, division of fractions also involves four basic steps:

1. Finding the reciprocal or the multiplicative inverse of the second fraction (the divisor)
2. Changing the sign from division to multiplication
3. Multiplying the first fraction by the reciprocal fraction
4. Simplifying or reducing the quotient to its lowest terms if needed.

If a fraction ${\dfrac{a}{b}}$ is divided by another fraction ${\dfrac{x}{y}}$, then it is written as

${\dfrac{a}{b}\div \dfrac{x}{y}}$ = ${\dfrac{a}{b}\times \dfrac{y}{x}}$ 

This implies ${\dfrac{a\times y}{b\times x}}$ = ${\dfrac{ay}{bx}}$

Now, let us divide ${\dfrac{3}{5}}$ by ${\dfrac{3}{4}}$

${\dfrac{3}{5}\div \dfrac{3}{4}}$

Finding the Reciprocal

The second fraction is ${\dfrac{3}{4}}$

Turning ${\dfrac{3}{4}}$ upside down, we get the reciprocal

${\dfrac{3}{4}}$ becomes ${\dfrac{4}{3}}$

Changing the Sign

The sign is changed from division to multiplication

${\dfrac{3}{5}\times \dfrac{4}{3}}$

Multiplying the First Fraction by the Reciprocal

= ${\dfrac{3\times 4}{5\times 3}}$

= ${\dfrac{4}{5}}$

Simplifying 

Since ${\dfrac{4}{5}}$ is already in the simplified form.

Thus, the quotient is ${\dfrac{4}{5}}$

Visual Representation

Now, if we need to find 12 ÷ 4, it intends to find “How many 4s are there in 12?” 

Since 4 × 3 = 12, we find three 4s in 12. Thus, the answer is 3

Similarly, ${\dfrac{1}{2}\div \dfrac{1}{4}}$ means, “How many ${\dfrac{1}{4}}$s are in ${\dfrac{1}{2}}$?”

Let us use a circle to get the result.

With Whole Numbers

To divide a fraction by a whole number, we multiply the fraction by the reciprocal of the whole number and then simplify the quotient to its lowest terms if needed. 

Let us divide ${\dfrac{15}{4}}$ by ${5}$

${\dfrac{15}{4}\div 5}$

Finding the Reciprocal

The reciprocal of ${5}$ is ${\dfrac{1}{5}}$

Changing the Sign

= ${\dfrac{15}{4}\times \dfrac{1}{5}}$

Multiplying the First Fraction by the Reciprocal

= ${\dfrac{15\times 1}{4\times 5}}$

Simplifying 

= ${\dfrac{5\times 3\times 1}{4\times 5}}$

= ${\dfrac{3}{4}}$

Thus, the quotient is ${\dfrac{3}{4}}$

With Decimals

To divide a fraction by a decimal number, we first convert the given decimal to its equivalent fraction and then divide it by the given fraction.

Let us divide the fraction ${\dfrac{5}{6}}$ by the decimal number ${0\cdot 2}$

Converting the Decimal into Fraction

Converting ${0\cdot 2}$ into its equivalent fraction, we get

${0\cdot 2}$ = ${\dfrac{2}{10}}$ = ${\dfrac{1}{5}}$

Now, dividing ${\dfrac{5}{6}}$ by ${\dfrac{1}{5}}$, we have

${\dfrac{5}{6}\div \dfrac{1}{5}}$

Finding the Reciprocal

The reciprocal of ${\dfrac{1}{5}}$ is ${\dfrac{5}{1}}$

Changing the Sign

= ${\dfrac{5}{6}\times \dfrac{5}{1}}$

Multiplying the First Fraction by the Reciprocal

= ${\dfrac{5\times 5}{6\times 1}}$

= ${\dfrac{25}{6}}$, which is in the simplest form.

Thus, the quotient is ${\dfrac{25}{6}}$

With Mixed Numbers

To divide a fraction by a mixed number, we first convert the mixed number into an improper fraction and then follow the other steps.

If ${\dfrac{12}{7}\div 1\dfrac{2}{3}}$

Converting the Mixed Number into an Improper Fraction

Converting ${1\dfrac{2}{3}}$ into an improper fraction,

${1\dfrac{2}{3}}$ = ${\dfrac{\left( 1\times 3\right) +2}{3}}$ = ${\dfrac{5}{3}}$

Now, we have ${\dfrac{12}{7}\div \dfrac{5}{3}}$

Finding the Reciprocal

The reciprocal of ${\dfrac{5}{3}}$ is ${\dfrac{3}{5}}$

Changing the Sign

${\dfrac{12}{7}\times \dfrac{3}{5}}$

Multiplying the First Fraction by the Reciprocal

= ${\dfrac{12\times 3}{7\times 5}}$

= ${\dfrac{36}{35}}$, which is in the simplest form.

Thus, the quotient is ${\dfrac{36}{35}}$

Here is a summary of what we learned so far.

Solved Examples