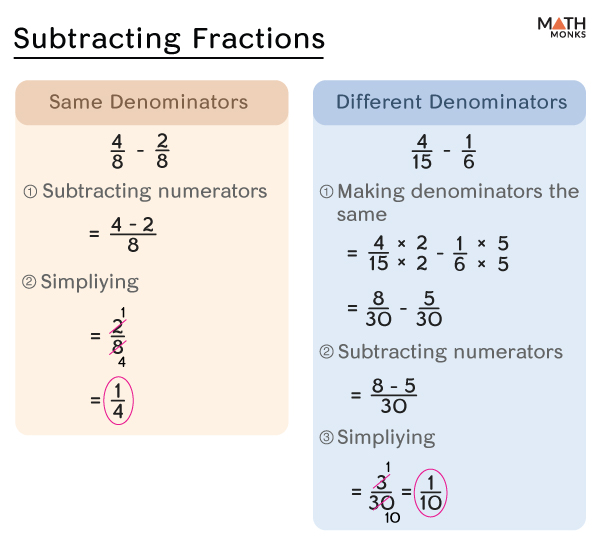
Subtracting fractions involves three basic steps:
- Identifying whether the denominators are the same. If they are the same, we move to step 2. If they are different, we find their common denominators.
- Subtracting the numerators
- Simplify the result if needed.
With Like Denominators
To subtract fractions with the same denominators, we subtract only the numerators and write the difference over the common denominator.
Let us subtract the fractions ${\dfrac{4}{7}-\dfrac{2}{7}}$
Identifying the Denominators
Here, the denominators are 7
Subtracting the Numerators
${\dfrac{4-2}{7}}$
= ${\dfrac{2}{7}}$, which can not be simplified or reduced further.
Thus, the difference is ${\dfrac{2}{7}}$
Problem – Subtracting from a NEGATIVE FRACTION
![]()
Subtract: ${-\dfrac{6}{11}-\dfrac{3}{11}}$
Solution:
![]()
Given, ${-\dfrac{6}{11}-\dfrac{3}{11}}$
= ${\dfrac{6-3}{11}}$
= ${\dfrac{3}{11}}$
Thus, the difference is ${\dfrac{3}{11}}$
With Unlike Denominators
Let us subtract the unlike fractions ${\dfrac{4}{15}-\dfrac{1}{6}}$
Identifying the Denominators
Here, the denominators are 15 and 6, that are different.
Finding the LCM of the Denominators
The LCM of 15 and 6 is 30
Making the Denominators the Same
Converting ${\dfrac{4}{15}}$ and ${\dfrac{1}{6}}$ to their equivalent fractions with 30 as the denominator,
${\dfrac{4\times 2}{15\times 2}}$ = ${\dfrac{8}{30}}$
${\dfrac{1\times 5}{6\times 5}}$ = ${\dfrac{5}{30}}$
Now, we have ${\dfrac{8}{30}-\dfrac{5}{30}}$
Subtracting the Numerators
${\dfrac{8-5}{30}}$
= ${\dfrac{3}{30}}$
Simplifying
${\dfrac{3\div 3}{30\div 3}}$
= ${\dfrac{1}{10}}$
Thus, the difference is ${\dfrac{1}{10}}$
![]()
Subtract: ${\dfrac{11}{3}}$ from ${\dfrac{9}{2}}$
Solution:
![]()
The denominators are 2 and 3
The LCM of 2 and 3 is 6
Here, ${\dfrac{9}{2}-\dfrac{11}{3}}$
= ${\dfrac{9\times 3}{2\times 3}-\dfrac{11\times 2}{3\times 2}}$
= ${\dfrac{27}{6}-\dfrac{22}{6}}$
= ${\dfrac{27-22}{6}}$
= ${\dfrac{5}{6}}$
Thus, the difference is ${\dfrac{5}{6}}$
Problem – Subtracting NEGATIVE FRACTIONS
![]()
Subtract: ${\dfrac{2}{5}-\left( -\dfrac{1}{2}\right)}$
Solution:
![]()
The denominators are 5 and 2
The LCM of 5 and 2 is 10
Given, ${\dfrac{2}{5}-\left( -\dfrac{1}{2}\right)}$
= ${\dfrac{2\times 2}{5\times 2}-\dfrac{1\times 5}{2\times 5}}$
= ${\dfrac{4}{10}-\dfrac{5}{10}}$
= ${\dfrac{4-5}{10}}$
= ${\dfrac{-1}{10}}$
Thus, the difference is ${\dfrac{-1}{10}}$
With Whole Numbers
To subtract a fraction from a whole number, we convert the whole number into the fraction form and then follow the steps of subtracting fractions with unlike denominators.
Given ${3-\dfrac{1}{2}}$
Converting the Whole Number to Fraction
${\dfrac{3}{1}-\dfrac{1}{2}}$
Identifying the Denominators
Here, the denominators are 1 and 2
Finding the LCM of the Denominators
The LCM of 1 and 2 is 2
Subtracting the Numerators
${\dfrac{3}{1}-\dfrac{1}{2}}$
= ${\dfrac{3\times 2}{1\times 2}-\dfrac{1\times 1}{2\times 1}}$
= ${\dfrac{6}{2}-\dfrac{1}{2}}$
= ${\dfrac{6-1}{2}}$
= ${\dfrac{5}{2}}$
= ${2\dfrac{1}{2}}$
Thus, the difference is ${2\dfrac{1}{2}}$
With Mixed Numbers
To subtract mixed numbers, we first convert them into improper fractions and then subtract.
Given ${\dfrac{7}{3}-1\dfrac{1}{4}}$
Converting to Improper Fraction
= ${\dfrac{7}{3}-\dfrac{\left( 1\times 4\right) +1}{4}}$
= ${\dfrac{7}{3}-\dfrac{5}{4}}$
Identifying the Denominators
Here, the denominators are 3 and 4
Finding the LCM of the Denominators
The LCM of 3 and 4 is 12
Making the Denominators the Same and Subtracting the Numerators
${\dfrac{7\times 4}{3\times 4}-\dfrac{5\times 3}{4\times 3}}$
= ${\dfrac{28}{12}-\dfrac{15}{12}}$
= ${\dfrac{28-15}{12}}$
= ${\dfrac{13}{12}}$
= ${1\dfrac{1}{12}}$
Thus, the difference is ${1\dfrac{1}{12}}$
![]()
Subtract the following fractions: ${7\dfrac{1}{3}-2\dfrac{3}{4}}$
Solution:
![]()
Here, ${7\dfrac{1}{3}-2\dfrac{3}{4}}$
= ${\dfrac{\left( 7\times 3\right) +1}{3}-\dfrac{\left( 2\times 4\right) +3}{4}}$
= ${\dfrac{22}{3}-\dfrac{11}{4}}$
The denominators are 3 and 4
The LCM of 3 and 4 is 12
Now, we have
${\dfrac{22}{3}-\dfrac{11}{4}}$
= ${\dfrac{22\times 4}{3\times 4}-\dfrac{11\times 3}{4\times 3}}$
= ${\dfrac{88}{12}-\dfrac{33}{12}}$
= ${\dfrac{88-33}{12}}$
= ${\dfrac{55}{12}}$
= ${4\dfrac{7}{12}}$
Thus, the difference is ${4\dfrac{7}{12}}$
