Reciprocal of a Fraction

The reciprocal of a fraction, also known as the multiplicative inverse, is obtained by swapping or interchanging the numerator and the denominator. Multiplying the reciprocal with the original fraction gives 1.

Thus, the reciprocal of a fraction ${\dfrac{p}{q}}$ is ${\dfrac{q}{p}}$, where p and q are non-zero integers.

Examples

The reciprocal of ${\dfrac{2}{3}}$ is ${\dfrac{3}{2}}$ and ${\dfrac{1}{2}}$ is ${\dfrac{2}{1}}$ or ${2}$

Visual Representation

Now, if we need to find the reciprocal of ${\dfrac{1}{4}}$, it intends to find ‘The number of quarters that are there in a whole.’

Since 4 quarters make a whole, thus, four ${\dfrac{1}{4}}$ parts are in a whole.

Thus, the reciprocal of ${\dfrac{1}{4}}$ is ${\dfrac{4}{1}}$ or or ${4}$

When we multiply ${\dfrac{1}{4}}$ by its reciprocal ${4}$, we get

${\dfrac{1}{4}\times 4}$ = 1

For example, 

The reciprocal of ${\dfrac{2}{3}}$ is ${\dfrac{3}{2}}$ since ${\dfrac{2}{3}\times \dfrac{3}{2}}$ = 1

For Zero (0)

There is no value or number that, when multiplied by 0, results in 1. Thus, the reciprocal of 0 is always undefined, indicating that the value does not exist.

Thus ${\dfrac{1}{0}}$, ${\dfrac{22}{0}}$, or ${\dfrac{100}{0}}$ are undefined.

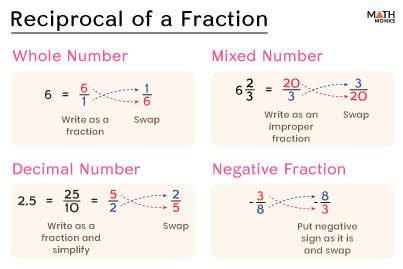
For Whole Number

To find the reciprocal of any non-zero number, we divide 1 by that number.

Let us find the reciprocal of ${5}$

Writing the Whole Number as a Fraction

${5}$ is written as a fraction: ${\dfrac{5}{1}}$

Interchanging the Numerator and Denominator

 ${5}$ on interchanging gives ${\dfrac{1}{5}}$

For Mixed Number

To find the reciprocal of a mixed number, we first convert the mixed number to an improper fraction and then find its reciprocal by interchanging the numerator and denominator.

Let us find the reciprocal of ${2\dfrac{1}{7}}$

Converting into Improper Fraction

${2\dfrac{1}{7}}$ = ${\dfrac{\left( 2\times 7\right) +1}{7}}$ = ${\dfrac{15}{7}}$

Interchanging the Numerator and Denominator

${\dfrac{15}{7}}$ on interchanging gives ${\dfrac{7}{15}}$

For Decimal Number

To find the reciprocal of a decimal number, we rewrite the decimal in the fraction form and then find its reciprocal.

Let us find the reciprocal of 0.5

Writing the Decimal as a Fraction

0.5 = ${\dfrac{5}{10}}$ = ${\dfrac{1}{2}}$

Interchanging the Numerator and Denominator

${\dfrac{2}{1}}$

Thus, the reciprocal of 0.5 is ${\dfrac{2}{1}}$ or ${2}$

For Negative Fraction

To find the reciprocal of a negative fraction, we simply calculate the reciprocal of the positive fraction and put the negative sign to it. 

If the negative fraction is ${\dfrac{-3}{5}}$

By interchanging the numerator and denominator

Here, the positive fraction is ${\dfrac{3}{5}}$

The reciprocal of ${\dfrac{3}{5}}$ is ${\dfrac{5}{3}}$

Keeping the negative sign

Thus, the reciprocal of the given fraction ${\dfrac{-3}{5}}$ is ${\dfrac{-5}{3}}$

With Exponents

To find the reciprocal of fractions with exponents, we first use the exponential laws to simplify the numerator and denominator and then calculate the reciprocal. 

In general, if the fractions with exponents are expressed as ${\left( \dfrac{a}{b}\right) ^{m}}$ which is equal to ${\dfrac{a^{m}}{b^{m}}}$

Then the reciprocal of ${\dfrac{a^{m}}{b^{m}}}$ is obtained just by swapping the numerator and denominator as ${\dfrac{b^{m}}{a^{m}}}$

Here, 

m is any rational number

a and b are any whole numbers

Here is the summary of what we learned so far.