Simplifying Fractions

Simplifying a fraction means reducing a fraction to its lowest form. A fraction is said to be in its simplest form if 1 is the only common factor of its numerator and denominator. For example,

${\dfrac{3}{5}}$ is in its simplest or lowest form since 1 is the only common factor of 3 and 5.

Equivalent Fractions Method

In this method, we first find the common factors of the numerator and denominator. Then, we divide both parts by their common factors until they have no common factor except 1.

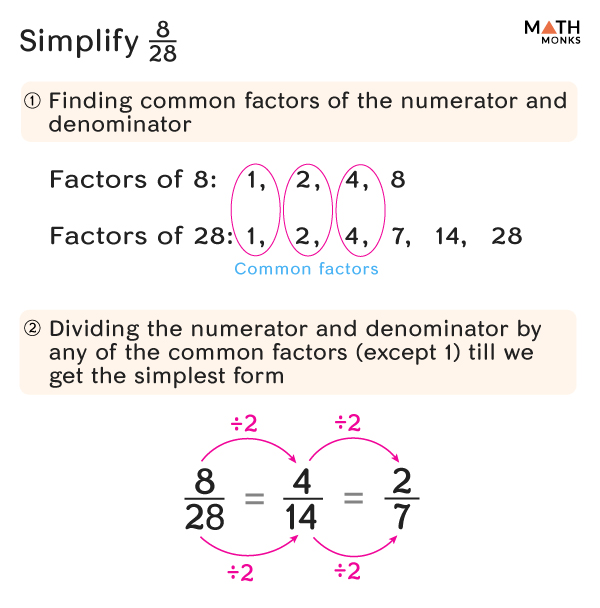
Let us simplify ${\dfrac{8}{28}}$

Finding the Factors of the Numerator and Denominator 

The factors of 8 are 1, 2, 4, 8

The factors of 28 are 1, 2, 4, 7, 14, 28

Determining the Common Factors of the Numerator and Denominator 

The common factors of 8 and 28 are 1, 2, and 4

Dividing the numerator and denominator by the common factors 

On dividing the numerator and denominator by 2, we get

${\dfrac{8\div 2}{28\div 2}=\dfrac{4}{14}}$

Again, by dividing the numerator and denominator by 2, we get

${\dfrac{4\div 2}{14\div 2}=\dfrac{2}{7}}$, which is in its simplest form.

Thus, ${\dfrac{8}{28}}$is simplified to ${\dfrac{2}{7}}$

Greatest Common Factor (GCF) Method

To simplify proper fractions, we first find the GCF (greatest common factor) of the numerator and denominator and then divide both by their GCF. 

Let us simplify the fraction ${\dfrac{18}{30}}$ 

Finding the GCF of the Numerator and Denominator 

The factors of 18 are 1, 2, 3, 6, 9, 18

The factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30

The GCF of 18 and 30 is 6

Dividing Both Numerator and Denominator by GCF

On dividing the numerator and denominator by 6, we get

${\dfrac{18\div 6}{30\div 6}=\dfrac{3}{5}}$

Here, 1 is the only common factor of 3 and 5

Thus, ${\dfrac{3}{5}}$ is in its simplest form.

Prime Factorization Method

In this method, we find prime factors of the numerator and denominator and cancel out the common factors from both parts.

Let us simplify the fraction ${\dfrac{42}{54}}$

Prime Factorizing the Numerator and Denominator 

${\dfrac{42}{54}}$ = ${\dfrac{2\times 3\times 7}{2\times 3\times 3\times 3}}$

Cancelling the Common Factors 

= ${\dfrac{7}{3\times 3}}$

= ${\dfrac{7}{9}}$, which is in its simplest form.

Thus, ${\dfrac{42}{54}}$ = ${\dfrac{7}{9}}$

For Improper Fractions

To simplify improper fractions, we divide the numerator and denominator by their GCF and then convert them to mixed numbers.

Let us simplify a fraction ${\dfrac{36}{24}}$

Finding the GCF of the Numerator and Denominator 

The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36

The factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24

The GCF of 36 and 24 is 12

Dividing Both Numerator and Denominator by GCF

On dividing the numerator and denominator by 12, we get

${\dfrac{36\div 12}{24\div 12}=\dfrac{3}{2}}$

Here, 1 is the only common factor of 3 and 2

Converting to Mixed Number

${\dfrac{3}{2}}$ = ${1\dfrac{1}{2}}$

Thus, ${1\dfrac{1}{2}}$ is in its simplest form.

For Mixed Numbers

To simplify the mixed numbers, we first divide the numerator and denominator of the fractional parts by finding their GCF and then write the whole and the simplified fraction together.

Let us simplify ${1\dfrac{8}{12}}$

Finding the GCF of the Numerator and Denominator 

The factors of 8 are 1, 2, 4, 8

The factors of 12 are 1, 2, 3, 4, 6, 12

The HCF of 8 and 12 is 4

Dividing Both Numerator and Denominator by GCF

On dividing the numerator and denominator by 4, we get

${\dfrac{8\div 4}{12\div 8}=\dfrac{2}{3}}$

Here, 1 is the only common factor of 2 and 3

Writing the Whole and the Simplified Fraction

Thus, the simplified number is ${1\dfrac{2}{3}}$

With Variables

We can also simplify fractions containing variables. To do so, we use the expanded form of each term in the numerator and denominator and then divide both parts by the common variables.

Let us simplify the fraction ${\dfrac{x^{4}y}{x^{2}y^{3}}}$

Expanding Both Numerators and Denominators 

${\dfrac{x^{4}y}{x^{2}y^{3}}}$ = ${\dfrac{x\times x\times x\times x\times y}{x\times x\times y\times y\times y}}$

Cancelling the Common Variables 

${\dfrac{x\times x\times x\times x\times y}{x\times x\times y\times y\times y}}$ = ${\dfrac{x\times x}{y\times y}}$ = ${\dfrac{x^{2}}{y^{2}}}$

Thus, ${\dfrac{x^{2}}{y^{2}}}$ is the simplified fraction.

With Exponents

To simplify the fraction containing exponents, we use the expanded form of exponents and then cancel the common factors.

Let us simplify the fraction ${\dfrac{2^{4}}{2^{2}}}$

Expanding Both Numerators and Denominators 

${\dfrac{2^{4}}{2^{2}}}$ = ${\dfrac{2\times 2\times 2\times 2}{2\times 2}}$

Cancelling the Common Factors 

${\dfrac{2\times 2\times 2\times 2}{2\times 2}}$ = ${2\times 2}$ = ${4}$ = ${\dfrac{4}{1}}$

Thus, ${4}$ or ${\dfrac{4}{1}}$ is in its simplest form.

Solved Examples