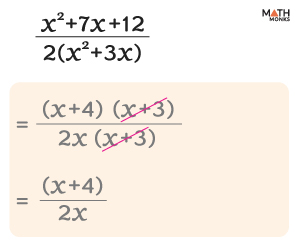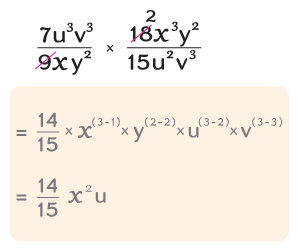An algebraic fraction is a type of fraction where the numerator, the denominator, or both contain at least one variable.
${\dfrac{x}{5}}$, ${\dfrac{3}{x}}$, ${\dfrac{x-7}{5}}$, and ${\dfrac{2}{x-11}}$ are a few examples of algebraic fractions.
Now, we will learn how to solve algebraic fractions with various operations here.
Reducing
Like reducing numeric fractions, to reduce algebraic fractions to their lowest term, we will eliminate the common factor of the numerator and denominator.
Let us reduce ${\dfrac{4x^{8}}{20x}}$ to its simplest form
${\dfrac{4x^{8}}{20x}}$
= ${\dfrac{4}{20}\times \dfrac{x^{8}}{x}}$
= ${\dfrac{1}{5}x^{7}}$ or ${\dfrac{x^{7}}{5}}$
We can also simplify complex algebraic fractions through the basic mathematical operations: addition, subtraction, multiplication, and division.
Adding
To add algebraic fractions, we need to have a common denominator. Once we have the same denominator, we can add the numerators.
Let us add the algebraic fractions ${\dfrac{3}{6x+18}}$ and ${\dfrac{10}{x+3}}$
${\dfrac{3}{6x+18}+\dfrac{10}{x+3}}$
Finding the Common Denominator
First, we will find the common denominator for (6x + 18) and (x + 3)
On multiplying each fraction by the denominator of the other fraction,
${\dfrac{3}{6x+18}+\dfrac{10}{x+3}}$
= ${\dfrac{3\left( x+3\right) }{6x+18}+\dfrac{10\left( 6x+18\right) }{x+3}}$
Adding the Numerators
= ${\dfrac{3\left( x+3\right) +10\left( 6x+18\right) }{\left( 6x+18\right) \left( x+3\right) }}$
Taking Out the Common Factors (If Needed)
Now, we will take out the common factors from the numerator and denominator
= ${\dfrac{3\left( x+3\right) +10\times 6\left( x+3\right) }{6\left( x+3\right) \left( x+3\right) }}$
= ${\dfrac{\left( x+3\right) \left( 3+60\right) }{6\left( x+3\right) \left( x+3\right) }}$
= ${\dfrac{63}{6\left( x+3\right) }}$
= ${\dfrac{21}{2\left( x+3\right) }}$
Thus, the sum is ${\dfrac{21}{2\left( x+3\right) }}$
Subtracting
Similar to adding, here we will follow the following steps:
${\dfrac{3}{6x+18}-\dfrac{10}{x+3}}$
Finding the Common Denominator
Multiplying each fraction by the denominator of the other fraction,
= ${\dfrac{3\left( x+3\right) }{6x+18}-\dfrac{10\left( 6x+18\right) }{x+3}}$
Subtracting the Numerators
= ${\dfrac{3\left( x+3\right) -10\left( 6x+18\right) }{\left( 6x+18\right) \left( x+3\right) }}$
Taking Out the Common Factors (If Needed)
= ${\dfrac{3\left( x+3\right) -10\times 6\left( x+3\right) }{6\left( x+3\right) \left( x+3\right) }}$
= ${\dfrac{\left( x+3\right) \left( 3-60\right) }{6\left( x+3\right) \left( x+3\right) }}$
= ${\dfrac{-57}{6\left( x+3\right) }}$
= ${\dfrac{-19}{2\left( x+3\right) }}$
Thus, the difference is ${\dfrac{-19}{2\left( x+3\right) }}$
Multiplying
Multiplying algebraic fractions follows the same rules as multiplying numerical fractions.
Let us multiply ${\dfrac{5x+20}{4}}$ and ${\dfrac{16}{\left( x+4\right) \left( x+2\right) }}$
${\dfrac{5x+20}{4}\times \dfrac{16}{\left( x+4\right) \left( x+2\right) }}$
Factoring the Numerator and Denominator
= ${\dfrac{5\left( x+4\right) }{4}\times \dfrac{16}{\left( x+4\right) \left( x+2\right) }}$
Taking Out the Common Factors
= ${5\times \dfrac{4}{\left( x+2\right) }}$
Multiplying the Numerators and Denominators
= ${\dfrac{20}{\left( x+2\right) }}$
Thus, the product is ${\dfrac{20}{\left( x+2\right) }}$
Dividing
It is similar to dividing numerical fractions.
Dividing ${\dfrac{8x^{12}}{3}}$ by ${\dfrac{2}{7}x^{8}}$
${\dfrac{8x^{12}}{3}\div \dfrac{2}{7}x^{8}}$
Multiplying the First Fraction by the Reciprocal of the Second Fraction
= ${\dfrac{8x^{12}}{3}\times \dfrac{7}{2x^{8}}}$
Factoring the Numerator and Denominator
= ${\dfrac{4\times 2\times x^{12}}{3}\times \dfrac{7}{2\times x^{8}}}$
Taking Out the Common Factors
= ${\dfrac{\left( 4\times 7\right) x^{\left( 12-8\right) }}{3}}$
Multiplying the Numerators and Denominators
= ${\dfrac{28x^{4}}{3}}$
Thus, the quotient is ${\dfrac{28x^{4}}{3}}$
Solved Examples
![]() Simplify: ${\dfrac{x^{2}+7x+12}{2\left( x^{2}+3x\right) }}$
Simplify: ${\dfrac{x^{2}+7x+12}{2\left( x^{2}+3x\right) }}$
Solution:
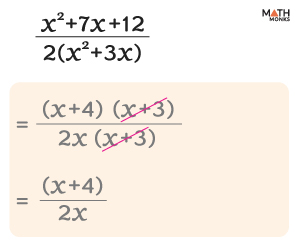
Thus, the algebraic fraction ${\dfrac{x^{2}+7x+12}{2\left( x^{2}+3x\right) }}$ is simplified to ${\dfrac{x+4}{2x}}$
![]() Multiply:
Multiply:
${\dfrac{7u^{3}v^{3}}{9xy^{2}}\times \dfrac{18x^{3}y^{2}}{15u^{2}v^{3}}}$
Solution:
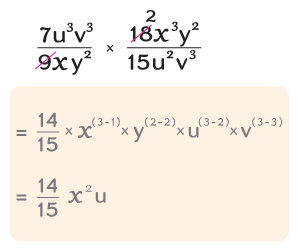
Thus, the product is ${\dfrac{14}{15}x^{2}u}$