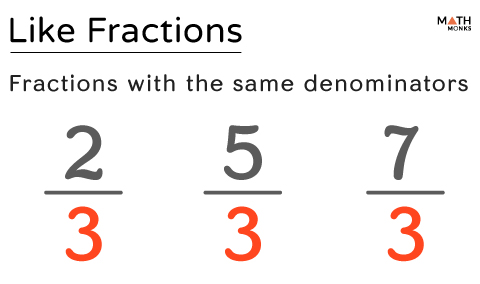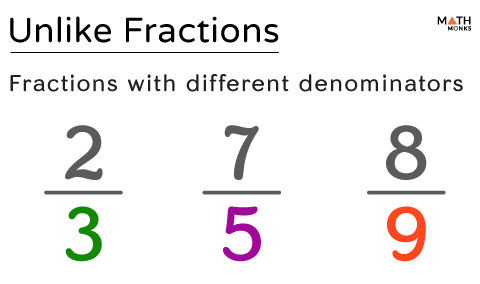Table of Contents
Last modified on June 21st, 2024
Fractions are classified into different types based on their numerators and denominators.
A fraction in which the numerator is less than its denominator is called a proper fraction. Its value is always less than 1.
${\dfrac{2}{3}}$, ${\dfrac{4}{5}}$, and ${\dfrac{2}{7}}$ are a few examples of proper fractions.
An improper fraction is a fraction in which the numerator is greater than or equal to its denominator. The value of a proper fraction is always greater than or equal to 1.
${\dfrac{3}{2}}$, ${\dfrac{5}{4}}$, ${\dfrac{7}{2}}$, and ${\dfrac{9}{9}}$ are a few examples of improper fractions.
A mixed fraction consists of a whole number and a proper fraction. Thus, they are always greater than 1.
${1\dfrac{2}{3}}$ and ${2\dfrac{3}{5}}$ are some examples of mixed fractions.
Fractions with the same denominators are called like fractions.
${\dfrac{2}{3}}$, ${\dfrac{5}{3}}$, ${\dfrac{7}{3}}$, and ${\dfrac{8}{3}}$ are a few like fractions.
Simplifying such fractions is easy, as the denominators of all the fractions are the same.
For example,
${\dfrac{2}{3}+\dfrac{5}{3}-\dfrac{7}{3}+\dfrac{8}{3}}$
= ${\dfrac{2+5-7+8}{3}}$
= ${\dfrac{8}{3}}$
Fractions with different denominators are known as unlike fractions.
${\dfrac{2}{3}}$, ${\dfrac{7}{5}}$, and ${\dfrac{7}{9}}$ are a few unlike fractions.
Simplifying such fractions involves factorizing the denominators before carrying out addition and subtraction.
For example,
${\dfrac{2}{3}+\dfrac{7}{5}}$
= ${\dfrac{2\times 5+7\times 3}{3\times 5}}$
= ${\dfrac{31}{15}}$
While multiplying, we first multiply the numerators and then the denominators.
For example,
${\dfrac{2}{3}\times \dfrac{7}{5}}$
= ${\dfrac{2\times 7}{3\times 5}}$
= ${\dfrac{14}{15}}$
In division, we multiply the dividend by the reciprocal of the divisor.
${\dfrac{2}{3}\div \dfrac{7}{5}}$
= ${\dfrac{2}{3}\times \dfrac{5}{7}}$
= ${\dfrac{2\times 5}{3\times 7}}$
= ${\dfrac{10}{21}}$
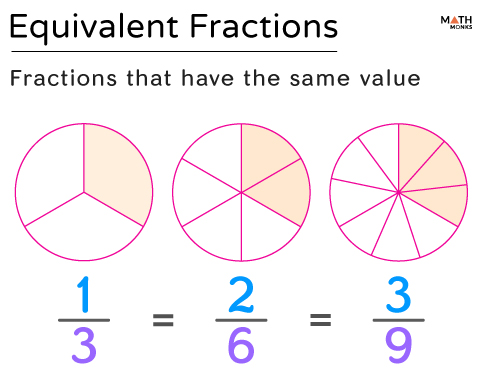
Equivalent fractions represent the same value after being simplified or reduced. To get equivalent fractions, we can multiply or divide the numerator and denominator of the given fraction by the same number.
For example,
${\dfrac{2}{3}}$ and ${\dfrac{6}{9}}$ are equivalent fractions.
Unit fractions are the fractions whose numerators are 1.
For example,
${\dfrac{1}{3}}$ and ${\dfrac{1}{9}}$ are unit fractions.
Here, we summarize the different types of fractions.
From the following fractions, identify the types of fractions as proper, improper, or mixed:
${\dfrac{1}{15}}$, ${1\dfrac{3}{8}}$, ${\dfrac{9}{3}}$, ${\dfrac{1}{7}}$, ${\dfrac{5}{5}}$, ${\dfrac{7}{3}}$
Here,
Proper fractions: ${\dfrac{1}{15}}$, ${\dfrac{1}{7}}$
Improper fractions: ${\dfrac{9}{3}}$, ${\dfrac{5}{5}}$, ${\dfrac{7}{3}}$
Mixed fraction: ${1\dfrac{3}{8}}$
Identify the like fractions:
${\dfrac{1}{5}}$, ${1\dfrac{3}{5}}$, ${\dfrac{9}{2}}$, ${\dfrac{2}{7}}$, ${\dfrac{3}{2}}$, ${\dfrac{10}{7}}$, ${\dfrac{10}{5}}$
Here,
${\dfrac{1}{5}}$, ${1\dfrac{3}{5}}$, and ${\dfrac{10}{5}}$ are like fractions.
${\dfrac{9}{2}}$ and ${\dfrac{3}{2}}$ are like fractions.
${\dfrac{2}{7}}$ and ${\dfrac{10}{7}}$ are like fractions.
Write two equivalent fractions of ${\dfrac{12}{15}}$
Here, ${\dfrac{12\div 3}{15\div 3}=\dfrac{4}{5}}$
${\dfrac{12\times 2}{15\times 2}=\dfrac{24}{30}}$
Thus, ${\dfrac{4}{5}}$ and ${\dfrac{24}{30}}$ are two equivalent fractions of ${\dfrac{12}{15}}$
Last modified on June 21st, 2024