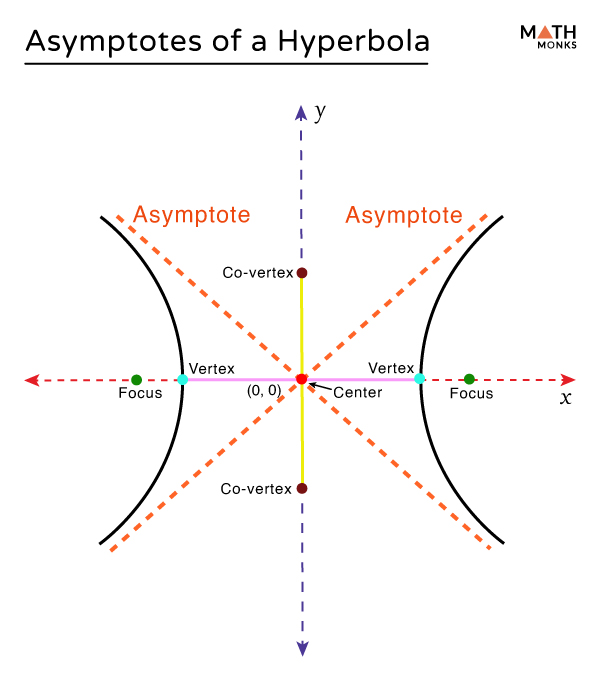
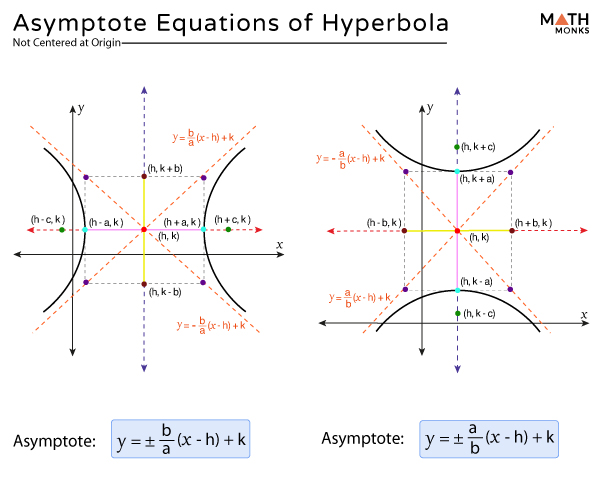
Asymptotes are straight lines that act as a boundary that the hyperbola approaches as it extends further from the center. Though the hyperbola gets closer and closer to the asymptotes as we move away from the center, it never intersects these lines.
Every hyperbola has two asymptotes, as shown.
Equations
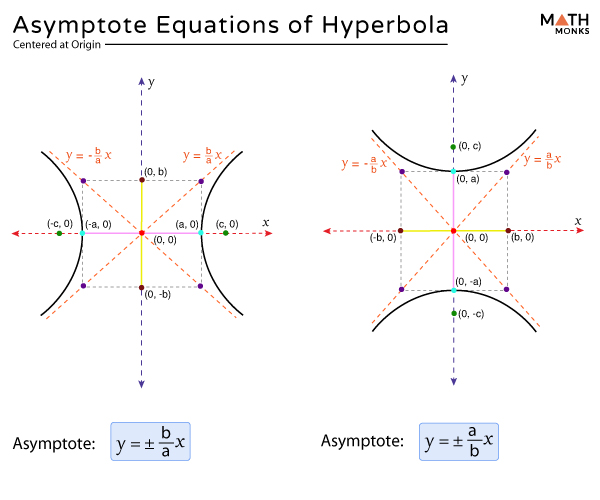
The equation of the asymptotes for a hyperbola depends on the form of the hyperbola’s equation. A hyperbola in standard form can be either horizontal or vertical, which determines the orientation of its asymptotes.
Standard Form – Centered at (0, 0)
Horizontal
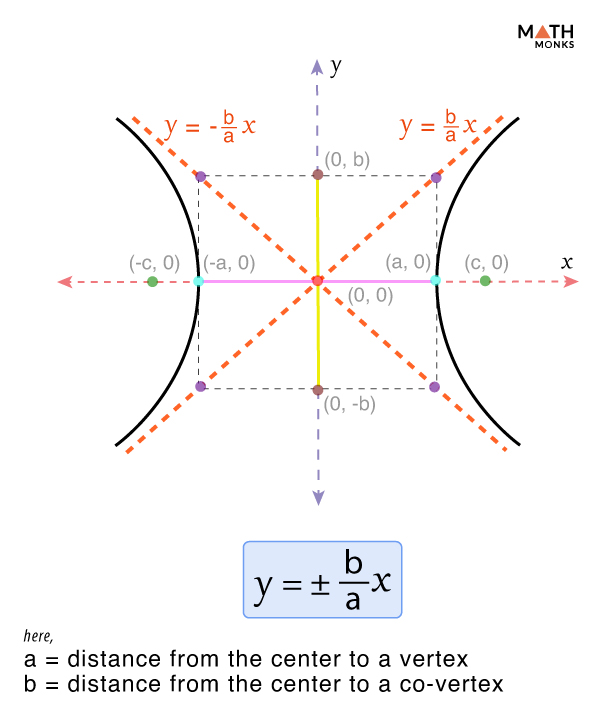
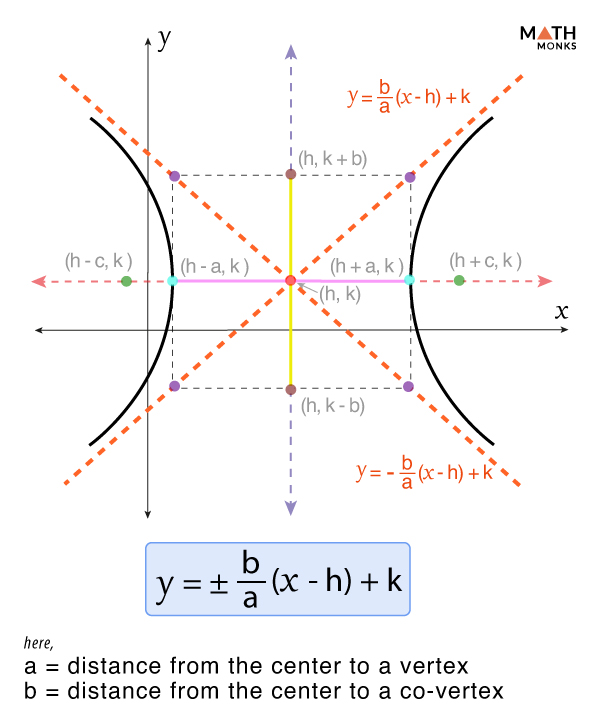
For a hyperbola of the form ${\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1}$ centered at (0, 0), its asymptotes are: ${y=\pm \dfrac{b}{a}x}$
Vertical
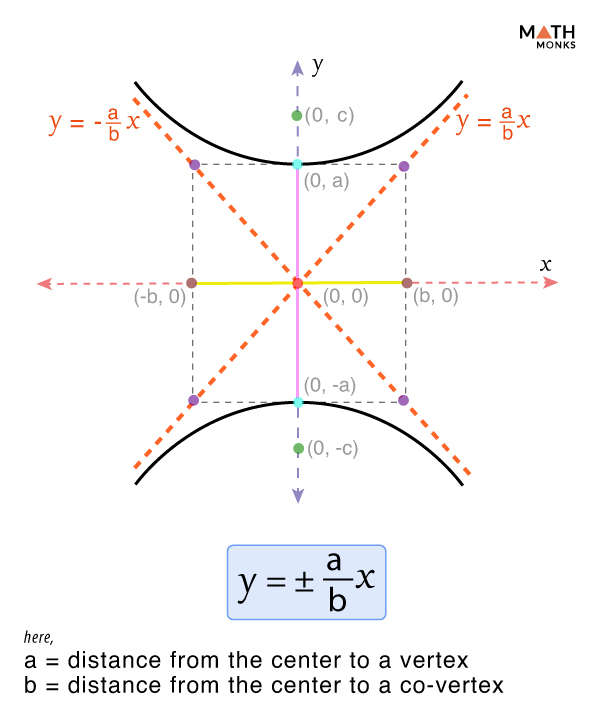
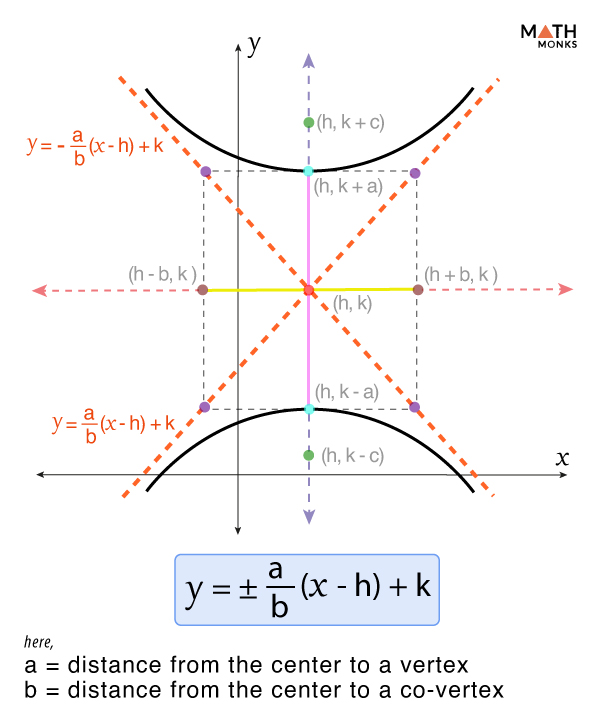
For a hyperbola of the form ${\dfrac{y^{2}}{a^{2}}-\dfrac{x^{2}}{b^{2}}=1}$ centered at (0, 0), its asymptotes are: ${y=\pm \dfrac{a}{b}x}$
Standard Form – Centered at (h, k)
Horizontal
For a hyperbola of the form ${\dfrac{\left( x-h\right) ^{2}}{a^{2}}-\dfrac{\left( y-k\right) ^{2}}{b^{2}}=1}$ centered at (h, k), its asymptotes are: ${y=\pm \dfrac{b}{a}\left( x-h\right) +k}$
Vertical
For a hyperbola of the form ${\dfrac{\left( y-k\right) ^{2}}{a^{2}}-\dfrac{\left( x-h\right) ^{2}}{b^{2}}=1}$ centered at (h, k), its asymptotes are: ${y=\pm \dfrac{a}{b}\left( x-h\right) +k}$
Here,
- a = the distance from the center to a vertex
- b = the distance from the center to the co-vertex
How To Find
By Factoring
Let us find the asymptote for the hyperbola ${\dfrac{x^{2}}{36}-\dfrac{y^{2}}{64}=1}$
Writing the Equation in the Standard Form
The equation ${\dfrac{x^{2}}{36}-\dfrac{y^{2}}{64}=1}$ is in its standard form. When an equation is not in the standard form, we convert the equation to standard form by completing the square.
Making the Equation Equal to 0 Instead of 1
${\dfrac{x^{2}}{36}-\dfrac{y^{2}}{64}=0}$
This equation represents both asymptotes.
Factoring the New Equation
${\left( \dfrac{x}{6}\right) ^{2}-\left( \dfrac{y}{8}\right) ^{2}=0}$
⇒ ${\left( \dfrac{x}{6}+\dfrac{y}{8}\right) \left( \dfrac{x}{6}-\dfrac{y}{8}\right) =0}$
Taking Each Factor and Solving for y
Now, ${\left( \dfrac{x}{6}+\dfrac{y}{8}\right) =0}$
⇒ ${\dfrac{8x+6y}{48}=0}$
⇒ ${8x+6y=0}$
⇒ ${y=-\dfrac{8}{6}x}$
⇒ ${y=-\dfrac{4}{3}x}$
Also, ${\left( \dfrac{x}{6}-\dfrac{y}{8}\right) =0}$
⇒ ${\dfrac{x}{6}=\dfrac{y}{8}}$
⇒ ${y=\dfrac{8}{6}x}$
⇒ ${y=\dfrac{4}{3}x}$
Thus, the asymptotes of the given hyperbola are ${y=-\dfrac{4}{3}x}$ and ${y=\dfrac{4}{3}x}$
![]() Find the asymptotes of the hyperbola 9y2 – 16x2 – 54y – 32x – 79 = 0
Find the asymptotes of the hyperbola 9y2 – 16x2 – 54y – 32x – 79 = 0
Solution:
![]()
Given, 9y2 – 16x2 – 54y – 32x – 79 = 0
⇒ (3y)2 – 2 ⋅ 3y ⋅ 9 + (9)2 – {(4x)2 + 2 ⋅ 4x ⋅ 4 + (4)2} – 144 = 0
⇒ (3y – 9)2 – (4x + 4)2 = 144
⇒ 9(y – 3)2 – 16(x + 1)2 = 144
⇒ ${\dfrac{9\left( y-3\right) ^{2}}{144}-\dfrac{16\left( x+1\right) ^{2}}{144}=1}$
⇒ ${\dfrac{\left( y-3\right) ^{2}}{16}-\dfrac{\left( x+1\right) ^{2}}{9}=1}$, which is in the standard form.
Now, by making the equation equal to 0 instead of 1, we get
${\dfrac{\left( y-3\right) ^{2}}{16}-\dfrac{\left( x+1\right) ^{2}}{9}=0}$
⇒ ${\left( \dfrac{y-3}{4}\right) ^{2}-\left( \dfrac{x+1}{3}\right) ^{2}=0}$
⇒ ${\left( \dfrac{y-3}{4}+\dfrac{x+1}{3}\right) \left( \dfrac{y-3}{4}-\dfrac{x+1}{3}\right) =0}$
Now, ${\left( \dfrac{y-3}{4}+\dfrac{x+1}{3}\right) =0}$
⇒ ${\dfrac{y-3}{4}=-\dfrac{x+1}{3}}$
⇒ ${y=-\dfrac{4}{3}\left( x+1\right) +3}$
Also, ${\left( \dfrac{y-3}{4}-\dfrac{x+1}{3}\right) =0}$
⇒ ${\dfrac{y-3}{4}=\dfrac{x+1}{3}}$
⇒ ${y=\dfrac{4}{3}\left( x+1\right) +3}$
Thus, the asymptotes of the given hyperbola are ${y=-\dfrac{4}{3}\left( x+1\right) +3}$ and ${y=\dfrac{4}{3}\left( x+1\right) +3}$
By Solving for y
Now, we will find the asymptote of the hyperbola ${\dfrac{\left( x-3\right) ^{2}}{4}-\dfrac{\left( y-1\right) ^{2}}{25}=1}$ by a different method.
Here, we will rewrite the equation in terms of y and then solve to get the asymptotes.
Writing the Equation With the y2 Term on the Left Side
${\left( y-1\right) ^{2}=25\left[ \dfrac{\left( x-3\right) ^{2}}{4}-1\right]}$
⇒ ${\left( y-1\right) ^{2}=\dfrac{25\left( x-3\right) ^{2}}{4}-25}$
⇒ ${\left( y-1\right) ^{2}=\left[ \dfrac{5\left( x-3\right) }{2}\right] ^{2}-25}$
Taking the Square Root of Each Side
⇒ ${\sqrt{\left( y-1\right) ^{2}}=\sqrt{\left[ \dfrac{5\left( x-3\right) }{2}\right] ^{2}-25}}$
⇒ ${\left( y-1\right) =\pm \sqrt{\left[ \dfrac{5\left( x-3\right) }{2}\right] ^{2}-25}}$
Adjusting the Equation for Large Values of x
To find the asymptote equation, we focus only on x (since, for very large values, x approaches infinity). This allows us to ignore certain constants, as they have little impact compared to the x term.
⇒ ${\left( y-1\right) =\pm \sqrt{\left[ \dfrac{5\left( x-3\right) }{2}\right] ^{2}}}$
⇒ ${\left( y-1\right) =\pm \dfrac{5\left( x-3\right) }{2}}$
Solving for y
⇒ ${y=\pm \dfrac{5}{2}\left( x-3\right) +1}$
Thus, the asymptotes of the given hyperbola are ${y=\dfrac{5}{2}\left( x-3\right) +1}$ and ${y=-\dfrac{5}{2}\left( x-3\right) +1}$
![]() Find the asymptotes of ${\dfrac{y^{2}}{64}-\dfrac{x^{2}}{121}=1}$
Find the asymptotes of ${\dfrac{y^{2}}{64}-\dfrac{x^{2}}{121}=1}$
Solution:
![]()
Given, ${\dfrac{y^{2}}{64}-\dfrac{x^{2}}{121}=1}$, which is in its standard form.
Now, ${\dfrac{y^{2}}{64}-\dfrac{x^{2}}{121}=1}$
⇒ ${y^{2}=64\left( \dfrac{x^{2}}{121}+1\right)}$
⇒ ${\sqrt{y^{2}}=\sqrt{\dfrac{64}{121}x^{2}+64}}$
⇒ ${y=\pm \sqrt{\dfrac{64}{121}x^{2}+64}}$
If x → ∞, then 64 → 0
⇒ ${y=\pm \sqrt{\dfrac{64}{121}x^{2}}}$ (ignoring the constant term)
⇒ ${y=\pm \dfrac{8}{11}x}$
Thus, the asymptotes of the given hyperbola are ${y=\dfrac{8}{11}x}$ and ${y=-\dfrac{8}{11}x}$
Angle between Asymptotes
The asymptotes form an angle between them, known as the asymptotic angle.
For a hyperbola in standard form ${\dfrac{y^{2}}{a^{2}}-\dfrac{x^{2}}{b^{2}}=1}$, the asymptotic angle can be found using the formula:
${\theta =\tan ^{-1}\left( \dfrac{2ab}{a^{2}-b^{2}}\right)}$
Here,
a = the distance from the center to a vertex
b = the distance from the center to the co-vertex
Proof
As we know,
The equations of the asymptotes of the hyperbola are ${y=\dfrac{b}{a}x}$ and ${y=-\dfrac{b}{a}x}$
Now, the slopes of the asymptotes are ${m_{1}=\dfrac{b}{a}}$ and ${m_{2}=-\dfrac{b}{a}}$
The angle between the asymptotes is given by
${\tan \theta =\dfrac{m_{1}-m_{2}}{1+m_{1}m_{2}}}$
⇒ ${\tan \theta =\dfrac{\dfrac{b}{a}-\left( -\dfrac{b}{a}\right) }{1+\dfrac{b}{a}\left( -\dfrac{b}{a}\right) }}$
⇒ ${\tan \theta =\dfrac{\dfrac{2b}{a}}{1-\dfrac{b^{2}}{a^{2}}}}$
⇒ ${\tan \theta =\dfrac{2ab}{a^{2}-b^{2}}}$
⇒ ${\theta =\tan ^{-1}\left( \dfrac{2ab}{a^{2}-b^{2}}\right)}$
Which is the formula used to calculate the asymptote of a hyperbola.
![]() Find the angle between the asymptotes of the hyperbola ${\dfrac{x^{2}}{64}-\dfrac{y^{2}}{36}=1}$
Find the angle between the asymptotes of the hyperbola ${\dfrac{x^{2}}{64}-\dfrac{y^{2}}{36}=1}$
Solution:
![]()
Given, ${\dfrac{x^{2}}{64}-\dfrac{y^{2}}{36}=1}$
As we know, the standard equation of the hyperbola is
${\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1}$
On comparing both equations, we get
a = 8 and b = 6
Now, ${\theta =\tan ^{-1}\left( \dfrac{2ab}{a^{2}-b^{2}}\right)}$
⇒ ${\theta =\tan ^{-1}\left( \dfrac{2\times 8\times 6}{8^{2}-6^{2}}\right)}$
⇒ ${\theta =\tan ^{-1}\left( \dfrac{2\times 8\times 6}{28}\right)}$
⇒ ${\theta =\tan ^{-1}\left( \dfrac{24}{7}\right)}$
Thus, the angle between the asymptotes of the hyperbola is ${\theta =\tan ^{-1}\left( \dfrac{24}{7}\right)}$