Eccentricity of Hyperbola

The eccentricity of a hyperbola is defined as the ratio of the distance from any point on the hyperbola to its focus and the perpendicular distance from the same point to the nearest directrix.

Formula

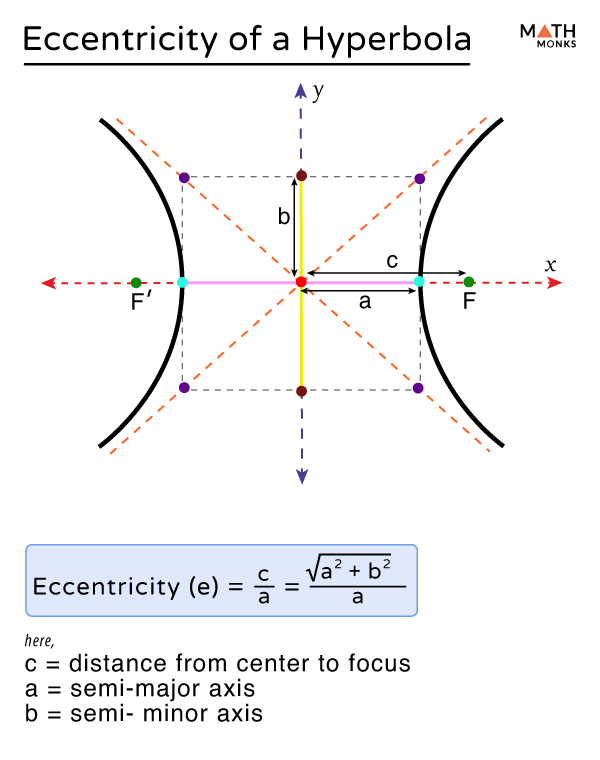
Mathematically, the eccentricity, denoted by e, in general form, is written as:

${e=\dfrac{c}{a}}$

Here, 

• c = distance from the center to the focus
• a = distance from the center to the vertex

The eccentricity of the hyperbola centered at the origin ${\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1}$, is given by:

${e=\dfrac{\sqrt{a^{2}+b^{2}}}{a}}$

Here, 

• a = distance from the center of the hyperbola to a vertex along the transverse axis
• b = distance from the center to a point on the conjugate axis

The eccentricity of the hyperbola is always greater than 1 (e > 1), which indicates that the distance from any point on the hyperbola to its focus is always greater than the distance from that point to the corresponding directrix.

Derivation

Let us consider a point P on the hyperbola with coordinates (x, y)

From the definition of hyperbola, we know the difference in the distances between a set of points present in a plane and two foci is always constant.

If the foci of the hyperbola are F (c, 0) and F’ (-c, 0), the difference in the distance from P to the foci F and F’ is 2a

PF’ – PF = 2a …..(i)

PF’ = ${\sqrt{\left( x+c\right) ^{2}+y^{2}}}$ and PF = ${\sqrt{\left( x-c\right) ^{2}+y^{2}}}$ …..(ii)

Now, substituting the values of (ii) in the equation (i), we get

${\sqrt{\left( x+c\right) ^{2}+y^{2}}-\sqrt{\left( x-c\right) ^{2}+y^{2}}=2a}$

⇒ ${\sqrt{\left( x+c\right) ^{2}+y^{2}}=2a+\sqrt{\left( x-c\right) ^{2}+y^{2}}}$

Squaring on both sides,

⇒ ${\left( x+c\right) ^{2}+y^{2}=4a^{2}+\left( x-c\right) ^{2}+y^{2}+4a\sqrt{\left( x-c\right) ^{2}+y^{2}}}$

⇒ ${x^{2}+c^{2}+2cx+y^{2}=4a^{2}+x^{2}+c^{2}-2cx+y^{2}+4a\sqrt{\left( x-c\right) ^{2}+y^{2}}}$

 Simplifying,

⇒ ${2cx=4a^{2}-2cx+4a\sqrt{\left( x-c\right) ^{2}+y^{2}}}$

⇒ ${4cx-4a^{2}=4a\sqrt{\left( x-c\right) ^{2}+y^{2}}}$

⇒ ${cx-a^{2}=a\sqrt{\left( x-c\right) ^{2}+y^{2}}}$

Again, on squaring both sides,

⇒ ${\left( cx-a^{2}\right) ^{2}=a^{2}\left\{ \left( x-c\right) ^{2}+y^{2}\right\}}$

⇒ c²x² + a⁴ – 2a²cx = a²(x² + c² – 2cx + y²)

Simplifying further, 

⇒ c²x² + a⁴ – 2a²cx = a²x² + a²c² – 2a²cx + a²y² 

⇒ c²x² + a⁴ = a²x² + a²c² + a²y² 

⇒ c²x² – a²x² – a²y² = a²c² – a⁴ 

⇒ x²(c² – a²) – a²y² = a²(c² – a²)

Dividing both sides by a²(c² – a²), 

⇒ ${\dfrac{x^{2}\left( c^{2}-a^{2}\right) }{a^{2}\left( c^{2}-a^{2}\right) }-\dfrac{a^{2}y^{2}}{a^{2}\left( c^{2}-a^{2}\right) }=\dfrac{a^{2}\left( c^{2}-a^{2}\right) }{a^{2}\left( c^{2}-a^{2}\right) }}$

⇒ ${\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{c^{2}-a^{2}}=1}$ …..(ii)

Since we know the standard equation of the hyperbola is ${\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1}$ …..(iii)

Now, on comparing the equations (ii) and (iii),

c² – a² = b²

⇒ c² = a² + b² 

⇒ c = ${\sqrt{a^{2}+b^{2}}}$ …..(iv)

Now, from the definition of the eccentricity, we get ${e=\dfrac{c}{a}}$ …..(v)

Now, substituting the value of c from (iv) in the equation (iii), we get

${e=\dfrac{\sqrt{a^{2}+b^{2}}}{a}}$, which is the formula to calculate eccentricity in terms of lengths of its major axis and minor axis.

Solved Examples