The equation of a hyperbola depends on its orientation and center. When classified by the orientation of the transverse axis, the hyperbola can be either horizontal or vertical. Additionally, each form varies depending on whether the center is at the origin or elsewhere. Thus, there are four possible cases to consider when graphing a hyperbola.
However, to graph any hyperbola, the following steps are followed:
- Writing the Equation in Standard Form (If Not Given)
- Identifying the Center
- Determining the Transverse Axis (Horizontal or Vertical)
- Finding the Vertices and Co-vertices
- Finding the Foci
- Finding the Asymptotes
- Sketching the Hyperbola
Horizontal Hyperbola – Centered at (0, 0)
The standard form of the equation for a horizontal hyperbola centered at (0, 0) is
${\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1}$
Here, the transverse axis is aligned along the x-axis, and the conjugate axis along the y-axis.
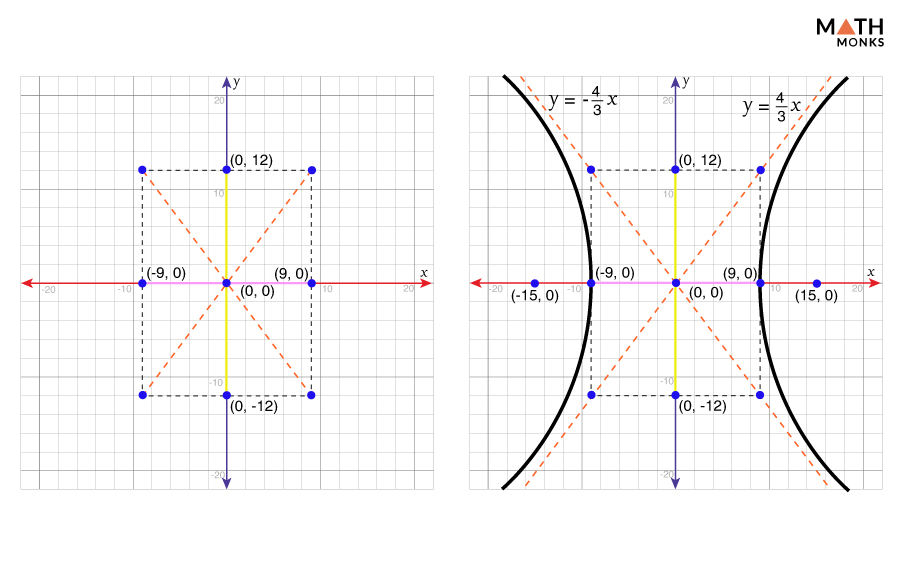
Let us graph the hyperbola ${\dfrac{x^{2}}{81}-\dfrac{y^{2}}{144}=1}$
Writing the Equation in Standard Form
In this case, the hyperbola is already in its standard form.
Identifying the Center
The center is at (0, 0)
Determining the Transverse Axis
Its transverse axis is aligned along the x-axis, and thus, it is a horizontal hyperbola.
Finding the Vertices and Co-vertices
The coordinates of the vertices are (±a, 0) = (-9, 0) and (9, 0)
The coordinates of the co-vertices are (0, ±b) = (0, 12) and (0, -12)
Finding the Foci
Since c = ${\sqrt{a^{2}+b^{2}}}$
⇒ c = ${\sqrt{9^{2}+12^{2}}}$ = ${\sqrt{225}}$ = ${15}$
The coordinates of the foci are (±c, 0) = (-15, 0) and (15, 0)
Finding the Asymptotes
The equations of the asymptotes are
y = ${\pm \dfrac{b}{a}x}$ = ${\pm \dfrac{12}{9}x}$ ⇒ y = ${\pm \dfrac{4}{3}x}$
Sketching the Hyperbola
We will now plot the vertices and co-vertices, then draw a central rectangle with sides parallel to the axes, passing through these points. The diagonals are extended, forming the asymptotes. This central rectangle and the asymptotes help shape the hyperbola graph accurately. Finally, the foci and asymptotes are marked, and a smooth curve is traced, as shown.
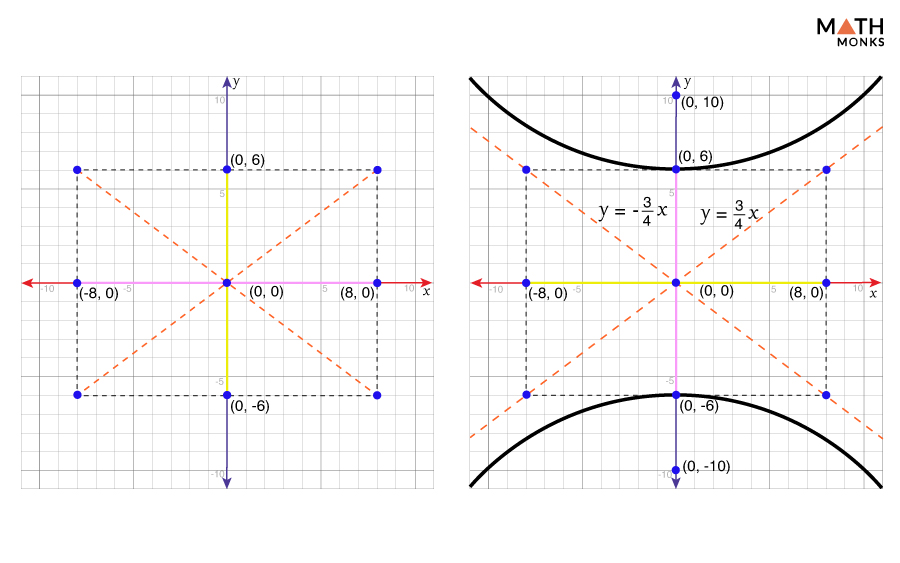
Vertical Hyperbola – Centered at (0, 0)
The standard form of the equation for a vertical hyperbola centered at (0, 0) is ${\dfrac{y^{2}}{a^{2}}-\dfrac{x^{2}}{b^{2}}=1}$
Here, the transverse axis is aligned along the y-axis, and the conjugate axis along the x-axis.
Let us graph the hyperbola ${\dfrac{x^{2}}{81}-\dfrac{y^{2}}{144}=1}$
Writing the Equation in Standard Form
In this case, the hyperbola is already in its standard form.
Identifying the Center
The center is at (0, 0)
Determining the Transverse Axis
Its transverse axis is aligned along the y-axis, and thus, it is a vertical hyperbola.
Finding the Vertices and Co-vertices
The coordinates of the vertices are (0, ±a) = (0, 6) and (0, -6)
The coordinates of the co-vertices are (±b, 0) = (-8, 0) and (8, 0)
Finding the Foci
Since c = ${\sqrt{a^{2}+b^{2}}}$
⇒ c = ${\sqrt{6^{2}+8^{2}}}$ = ${\sqrt{100}}$ = ${10}$
The coordinates of the foci are (0, ±c) = (0, 10) and (0, -10)
Finding the Asymptotes
The equations of the asymptotes are
y = ${\pm \dfrac{a}{b}x}$ = ${\pm \dfrac{6}{8}x}$ ⇒ y = ${\pm \dfrac{3}{4}x}$
Sketching the Hyperbola
Now, plotting the vertices, co-vertices, and asymptotes and then drawing the central rectangle, we get:
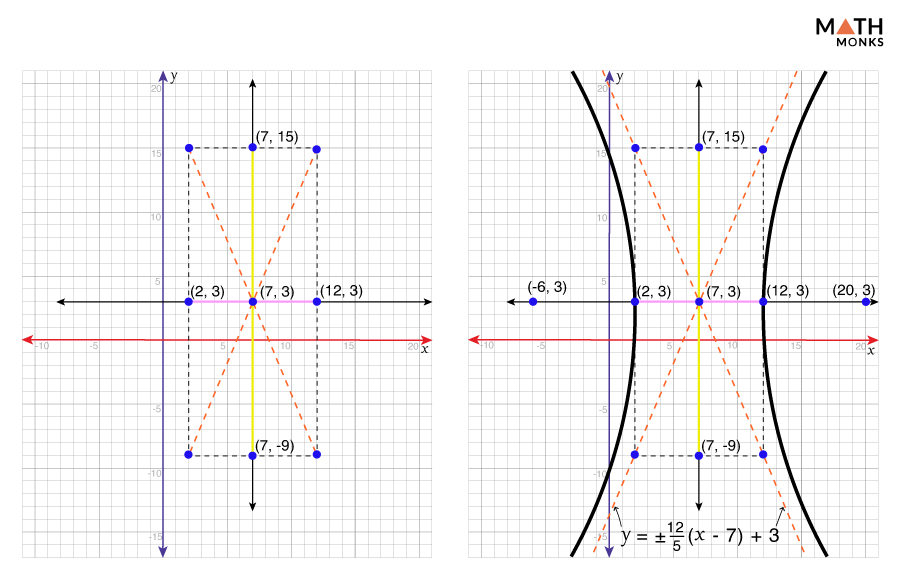
Horizontal Hyperbola – Centered at (h, k)
The standard form of the equation for a horizontal hyperbola centered at (h, k) is ${\dfrac{\left( x-h\right) ^{2}}{a^{2}}-\dfrac{\left( y-k\right) ^{2}}{b^{2}}=1}$
Here, the transverse axis is parallel to the x-axis.
Let us graph the hyperbola ${\dfrac{\left( x-7\right) ^{2}}{25}-\dfrac{\left( y-3\right) ^{2}}{144}=1}$
Writing the Equation in Standard Form
Here, the hyperbola is already in its standard form.
Identifying the Center
The center is at (h, k) = (7, 3)
Determining the Transverse Axis
Its transverse axis is parallel to the x-axis, and thus, it is a horizontal hyperbola.
Finding the Vertices and Co-vertices
The coordinates of the vertices are (h ± a, k) = (7 ± 5, 3) = (2, 3) and (12, 3)
The coordinates of the co-vertices are (h, k ± b) = (7, 3 ± 12) = (7, -9) and (7, 15)
Finding the Foci
Since c = ${\sqrt{a^{2}+b^{2}}}$
⇒ c = ${\sqrt{5^{2}+12^{2}}}$ = ${\sqrt{169}}$ = ${13}$
The coordinates of the foci are (h ± c, k) = (7 ± 13, 3) = (-6, 3) and (20, 3)
Finding the Asymptotes
The equations of the asymptotes are
y = ${\pm \dfrac{b}{a}\left( x-h\right) +k}$ = ${\pm \dfrac{12}{5}\left( x-7\right) +3}$
Sketching the Hyperbola
Now, plotting the vertices, co-vertices, and asymptotes and then drawing the central rectangle, we get
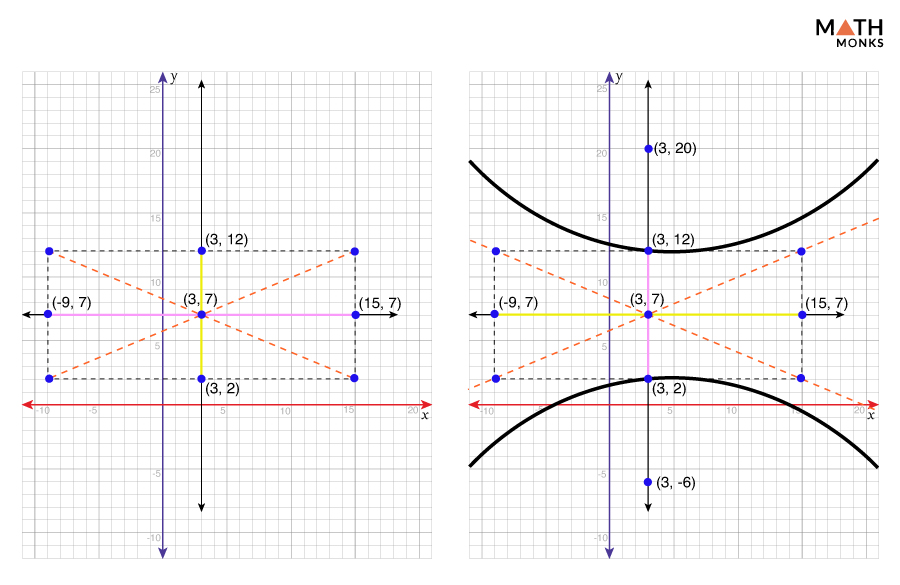
Vertical Hyperbola – Centered at (h, k)
The standard form of the equation for a horizontal hyperbola centered at (h, k) is ${\dfrac{\left( y-k\right) ^{2}}{a^{2}}-\dfrac{\left( x-h\right) ^{2}}{b^{2}}=1}$
Here, the transverse axis is parallel to the y-axis.
Let us graph the hyperbola ${\dfrac{\left( y-7\right) ^{2}}{25}-\dfrac{\left( x-3\right) ^{2}}{144}=1}$
Writing the Equation in Standard Form
Here, the hyperbola is already in its standard form.
Identifying the Center
The center is at (h, k) = (3, 7)
Determining the Transverse Axis
Its transverse axis is parallel to the y-axis, and thus, it is a vertical hyperbola.
Finding the Vertices and Co-vertices
The coordinates of the vertices are (h, k ± a) = (3, 7 ± 5) = (3, 2) and (3, 12)
The coordinates of the co-vertices are (h ± b, k) = (3 ± 12, 7) = (-9, 7) and (15, 7)
Finding the Foci
Since c = ${\sqrt{a^{2}+b^{2}}}$
⇒ c = ${\sqrt{5^{2}+12^{2}}}$ = ${\sqrt{169}}$ = ${13}$
The coordinates of the foci are (h, k ± c) = (3, 7 ± 13) = (3, -6) and (3, 20)
Finding the Asymptotes
The equations of the asymptotes are
y = ${\pm \dfrac{a}{b}\left( x-h\right) +k}$ = ${\pm \dfrac{5}{12}\left( x-3\right) +7}$
Sketching the Hyperbola
Now, plotting the vertices, co-vertices, and asymptotes and then drawing the central rectangle, we get
![]() Graph the hyperbola ${\dfrac{x^{2}}{49}-\dfrac{y^{2}}{9}=1}$
Graph the hyperbola ${\dfrac{x^{2}}{49}-\dfrac{y^{2}}{9}=1}$
Solution:
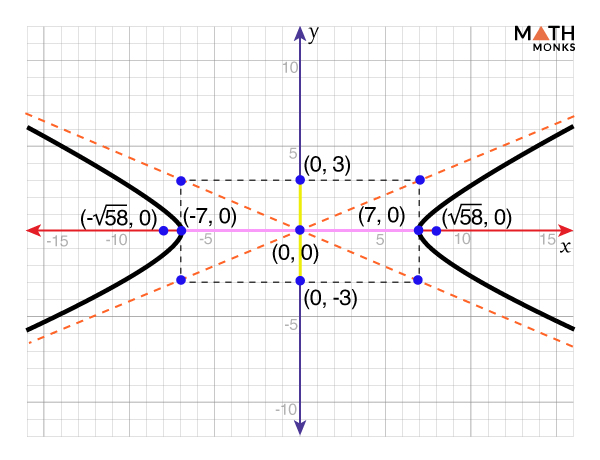
Given, ${\dfrac{x^{2}}{49}-\dfrac{y^{2}}{9}=1}$
Here,
a = 7, b = 3, and the transverse axis is along the x-axis.
As we know, the standard equation of a hyperbola with the center (0, 0) is
${\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1}$
Here,
The coordinates of the vertices are (±a, 0) = (±7, 0)
The coordinates of the co-vertices are (0, ±b) = (0, ±3)
Since c2 = a2 + b2
⇒ c = ${\sqrt{a^{2}+b^{2}}}$
⇒ c = ${\sqrt{7^{2}+3^{2}}}$ = ${\sqrt{49+9}}$ = ${\sqrt{58}}$
The coordinates of the foci are (±c, 0) = (${\pm \sqrt{58}}$, 0)
The equations of the asymptotes are y = ${\pm \dfrac{b}{a}x}$ = ${\pm \dfrac{3}{7}x}$
By plotting the vertices, co-vertices, foci, and asymptotes on the curves, we get the hyperbola alongside.
Problem – Graphing the hyperbola given by an equation NOT in STANDARD FORM.
![]() Graph the hyperbola 16x2 – 9y2 – 32x + 72y – 272 = 0. Find its center, vertices, co-vertices, foci, and asymptotes.
Graph the hyperbola 16x2 – 9y2 – 32x + 72y – 272 = 0. Find its center, vertices, co-vertices, foci, and asymptotes.
Solution:
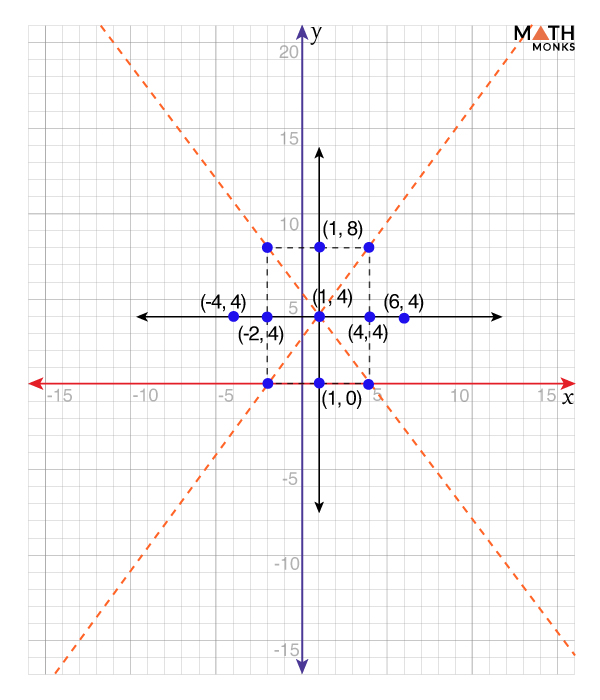
Given, 16x2 – 9y2 – 32x + 72y – 272 = 0
Converting the equation in the standard form,
16x2 – 32x – 9y2 + 72y – 272 = 0
⇒ (4x)2 – 2 ⋅ 4x ⋅ 4 + (4)2 – {(3y)2 – 2 ⋅ 3y ⋅ 12 + (12)2} -144 = 0
⇒ (4x – 4)2 – (3y – 12)2 = 144
⇒ 16(x – 1)2 – 9(y – 4)2 = 144
⇒ ${\dfrac{16\left( x-1\right) ^{2}}{144}-\dfrac{9\left( y-4\right) ^{2}}{144}=\dfrac{144}{144}}$
⇒ ${\dfrac{\left( x-1\right) ^{2}}{9}-\dfrac{\left( y-4\right) ^{2}}{16}=1}$, which is the standard equation of a hyperbola in the form of ${\dfrac{\left( x-h\right) ^{2}}{a^{2}}-\dfrac{\left( y-k\right) ^{2}}{b^{2}}=1}$
Here, a = 3, b = 4, and the transverse axis is parallel to the x-axis.
Now,
The center is (h, k) = (1, 4)
The coordinates of the vertices are (h ± a, k) = (1 ± 3, 4) = (-2, 4) or (4, 4)
The coordinates of the co-vertices are (h, k ± b) = (1, 4 ± 4) = (1, 0) or (1, 8)
Since c2 = a2 + b2 ⇒ c = ${\sqrt{a^{2}+b^{2}}}$ = ${\sqrt{3^{2}+4^{2}}}$ = ${\sqrt{25}}$ = 5
The coordinates of the foci are (h ± c, k)= (1 ± 5, 4) = (-4, 4) or (6, 4)
The equations of the asymptotes are y = ${\pm \dfrac{b}{a}\left( x-h\right) +k}$ = ${\pm \dfrac{4}{3}\left( x-1\right) +4}$
By plotting the center, vertices, co-vertices, foci, and asymptotes on the curves, we get the hyperbola alongside.
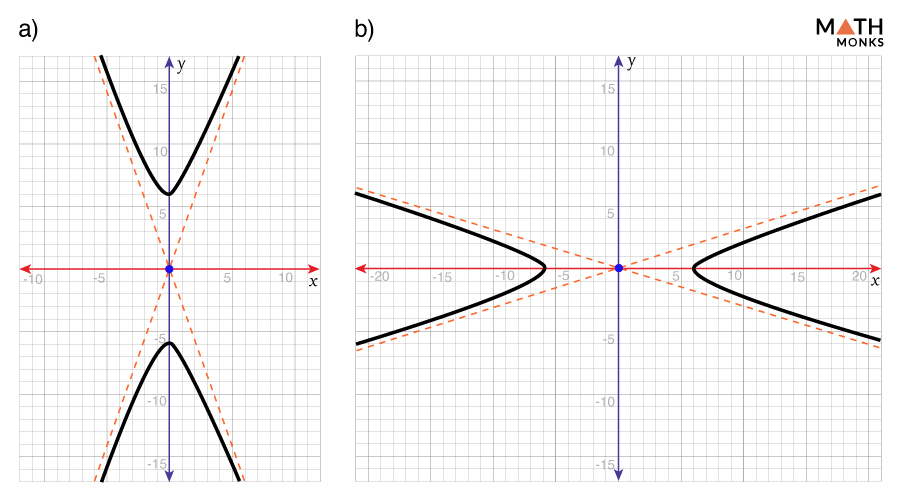 Which graph represents the hyperbola ${\dfrac{y^{2}}{36}-\dfrac{x^{2}}{4}=1}$?
Which graph represents the hyperbola ${\dfrac{y^{2}}{36}-\dfrac{x^{2}}{4}=1}$?
Solution:
![]()
Given, ${\dfrac{y^{2}}{36}-\dfrac{x^{2}}{4}=1}$
Here, its transverse axis is aligned along the y-axis.
Thus, option a) represents the given graph.



 Which graph represents the hyperbola ${\dfrac{y^{2}}{36}-\dfrac{x^{2}}{4}=1}$?
Which graph represents the hyperbola ${\dfrac{y^{2}}{36}-\dfrac{x^{2}}{4}=1}$?