Bernoulli Inequality

Bernoulli’s inequality (named after Jacob Bernoulli) approximates exponentiations of (1 + x) or more simply gives the approximation of (1 + x)ⁿ. 

Mathematically, the inequality is written as:

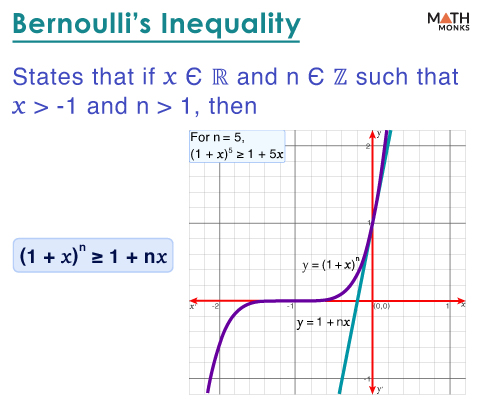
(1 + x)ⁿ ≥ 1 + nx, here ‘x’ is any real number greater than -1, and ‘n’ is any integer greater than 1

It is used to prove the convergence of sequences and series, providing an upper bound to show that the sequence converges to a particular limit and solves the critical limit problems easily.

Proof

Let us prove Bernoulli’s inequality using the process of mathematical induction.

Base Step

For n = 0, (1 + x)⁰ = 1 ≥ 1 + 0 ⋅ x, true

Inductive Step

Let us consider (1 + x)^k ≥ 1 + kx, for any integer n = k (> -1)

Now, assuming n = k + 1, we get

(1 + x)^{k + 1} = (1 + x)^k ⋅ (1 + x) ≥ (1 + kx) ⋅ (1 + x)

⇒ (1 + x)^{k + 1} ≥ (1 + kx) ⋅ (1 + x)

⇒ (1 + x)^{k + 1} ≥ 1 + kx + x + kx² 

⇒ (1 + x)^{k + 1} ≥ 1 + (k + 1)x + kx² ≥ 1 + (k + 1)x

⇒ (1 + x)^{k + 1} ≥ 1 + (k + 1)x

Thus, (1 + x)ⁿ ≥ 1 + nx, for any integer greater than -1

Hence, Bernoulli’s inequality is proved.

Alternate Proof

We can also prove Bernoulli’s inequality using the binomial theorem.

Case 1:

For x > 0, ${\left( 1+x\right) ^{n}=1+nx+\begin{pmatrix} n \\ 2 \end{pmatrix}x^{2}+\begin{pmatrix} n \\ 3 \end{pmatrix}x^{3}+\ldots +\begin{pmatrix} n \\ n \end{pmatrix}x^{n}\geq 1+nx}$ …..(i)

Case 2:

For x = 0, (1 + x)ⁿ ≥ 1 + nx, which is trivially true.

Case 3:

For -1 < x < 0, we consider y  = -x, then 0 < y < 1, and we have

${\left( 1-y\right) ^{n}=1-ny+\begin{pmatrix} n \\ 2 \end{pmatrix}y^{2}-\begin{pmatrix} n \\ 3 \end{pmatrix}y^{3}+\ldots +\left( -1\right) ^{n}\begin{pmatrix} n \\ n \end{pmatrix}y^{n}}$ …..(ii)

Putting y = 0, we get

${0=\left( 1-1\right) ^{n}=1-n+\begin{pmatrix} n \\ 2 \end{pmatrix}-\begin{pmatrix} n \\ 3 \end{pmatrix}+\ldots +\left( -1\right) ^{n}\begin{pmatrix} n \\ n \end{pmatrix}}$

⇒ ${\begin{pmatrix} n \\ 2 \end{pmatrix}-\begin{pmatrix} n \\ 3 \end{pmatrix}+\ldots +\left( -1\right) ^{n}\begin{pmatrix} n \\ n \end{pmatrix}=n-1 >0}$ …..(iii)

Since 0 < y < 1, y² > y³ > … > yⁿ 

Now, multiplying each term of (ii) by a factor that is smaller than its previous term, we get

${\begin{pmatrix} n \\ 2 \end{pmatrix}y^{2}-\begin{pmatrix} n \\ 3 \end{pmatrix}y^{3}+\ldots +\left( -1\right) ^{n}\begin{pmatrix} n \\ n \end{pmatrix}y^{n}\geq 0}$ …..(iv)

From (ii), (1 – y)ⁿ ≥ 1 – ny, for 0 < y < 1

⇒ (1 + x)ⁿ ≥ 1 + nx, for -1 < x < 0

Thus, Bernoulli’s inequality is proved.

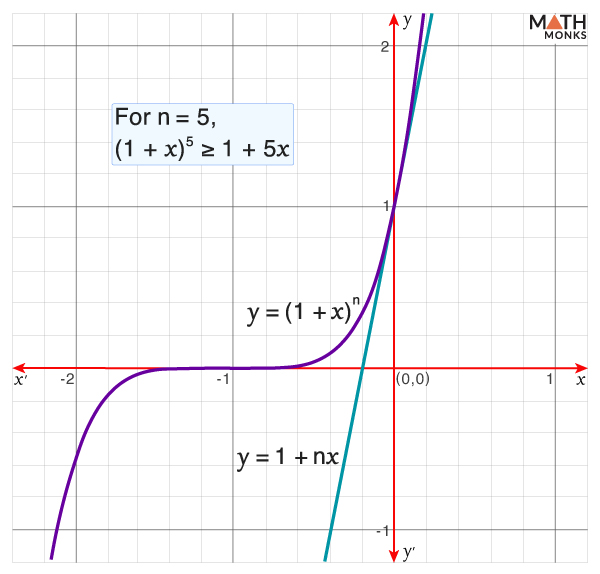
Graphical Representation

To verify Bernoulli’s inequality, here, we will plot the graphs of y = (1 + x)ⁿ and y = 1 + nx, for n = 5.

Solved Example