A rational inequality is a rational expression with an inequality sign and a fraction in either the numerator, denominator, or both.
${\dfrac{12}{x}\leq -4}$, ${\dfrac{2+x}{-7+x} >0}$, and ${\dfrac{3}{2-5x}\geq 8}$ are some examples of rational inequalities.
General Forms
If f(x) is a rational function, the four general forms of rational inequalities are:
- f(x) > 0
- f(x) < 0
- f(x) ≥ 0
- f(x) ≤ 0
Solving
While solving rational inequalities, we follow most of the steps we use in linear inequalities. We first write them in the general form and then find the critical values (or the zeros of both the numerator and the denominator). The solution is then plotted on the number line to verify the interval that satisfies the given inequality.
Additionally, we must remember that when multiplying and dividing by a negative number, the inequality sign reverses. Also, we must find the value(s), which might make the expression undefined.
Let us solve the rational inequality ${\dfrac{12}{x}\leq -4}$
Step 1: Converting into the General form
${\dfrac{12}{x}+4\leq 0}$
⇒ ${\dfrac{12+4x}{x}\leq 0}$ …..(i)
Step 2: Finding the Zeros of the Numerator and Denominator
Separating each factor equals to zero, we get
For the numerator,
12 + 4x = 0
⇒ 4x = -12
⇒ x = -3
For the denominator,
x = 0
Step 3: Dividing the Intervals and Verifying
This step involves choosing a number from each interval and substituting it with the original rational inequality to check its validity. If the result is true, the interval is part of the solution set. Otherwise, it is not.
Here, we picked up the numbers within the interval to check whether they satisfy the given inequality.
On verifying,
At x = -3, ${\dfrac{12+4\left( -3\right) }{-3}=\dfrac{12-12}{-3}=0}$, holds true.
At x = 0, ${\dfrac{12+4\left( 0\right) }{0}}$, which is undefined.
Step 4: Determining the Solution
Thus, the solution is -3 ≤ x < 0 or x Є [-3, 0) (in the interval notation)
Solved Examples
![]()
Solve the rational inequality: ${\dfrac{2+x}{x-7} >0}$
Solution:
Step 1: Converting into the General form
Here, the rational inequality ${\dfrac{2+x}{-7+x} >0}$ is already in its general form.
Step 2: Finding the Zeros of the Numerator and Denominator
For the numerator and denominator, we get
x + 2 = 0 and x – 7 = 0
⇒ x = -2 and x = 7
Step 3: Dividing the Intervals and Verifying
Now, verifying the intervals between the above critical points on the number line, we get
On verifying the given inequality at the critical points, we get
At x = -2, ${\dfrac{-2+2}{-2-7}=0}$, which means the result does not follow the inequality.
At x = 7, ${\dfrac{7+2}{7-7}}$, undefined.
Step 4: Determining the Solution
Thus, the solution is x Є (-∞, -2) ⋃ (7, ∞) (also written as x < -2 or x > 7)
![]()
Find the solution of the rational inequality ${\dfrac{x^{2}+2x-15}{\left( x+1\right) }\leq 0}$
Solution:
Here, ${\dfrac{x^{2}+2x-15}{\left( x+1\right) }\leq 0}$
Step 1: Converting into the General form
The given rational inequality is already in its general form.
Further simplifying the given inequality, we get
${\dfrac{x^{2}+5x-3x-15}{\left( x+1\right) }\leq 0}$
⇒ ${\dfrac{\left( x+5\right) \left( x-3\right) }{\left( x+1\right) }\leq 0}$
Step 2: Finding the Zeros of the Numerator and Denominator
For the numerator and denominator, we get
x + 5 = 0, x – 3 = 0, and x + 1 = 0
⇒ x = -5, x = 3, and x = -1
Step 3: Dividing the Intervals and Verifying
Now, verifying the intervals between the above critical points on the number line, we get
On verifying the general form of the given inequality at the critical points, we get
At x = -5, ${\dfrac{\left( -5+5\right) \left( -5-3\right) }{\left( -5+1\right) }=0}$, holds true
At x = -1, ${\dfrac{\left( -1+5\right) \left( -1-3\right) }{\left( -1+1\right) }}$, undefined
At x = 3, ${\dfrac{\left( 3+5\right) \left( 3-3\right) }{\left( 3+1\right) }=0}$, holds true
Step 4: Determining the Solution
Thus, the solution is either x ≤ -5 or -1 < x ≤ 3
![]()
Solve the rational inequality ${\dfrac{x^{2}-3x-4}{x^{2}-16}\geq 0}$
Solution:
Here, ${\dfrac{x^{2}-3x-4}{x^{2}-16}\geq 0}$
Step 1: Converting into the General form
The given rational inequality is already in its general form.
Further simplifying the given inequality, we get
${\dfrac{\left( x+1\right) \left( x-4\right) }{\left( x+4\right) \left( x-4\right) }\geq 0}$
Step 2: Finding the Zeros of the Numerator and Denominator
For the numerator, we get
x + 1 = 0 and x – 4 = 0
⇒ x = -1 and 4
For the denominator, we get
x + 4 = 0 and x – 4 = 0
⇒ x = -4 and 4
Step 3: Dividing the Intervals and Verifying
Now, verifying the intervals between the above critical points on the number line, we get
On verifying the general form of the given inequality at the critical points, we get
At x = -4, ${\dfrac{\left( -4+1\right) \left( -4-4\right) }{\left( -4+4\right) \left( -4-4\right) }}$, undefined.
At x = -1, ${\dfrac{\left( -1+1\right) \left( -1-4\right) }{\left( -1+4\right) \left( -1-4\right) }=0}$, holds true.
At x = 4, ${\dfrac{\left( 4+1\right) \left( 4-4\right) }{\left( 4+4\right) \left( 4-4\right) }}$, undefined.
Step 4: Determining the Solution
Thus, the solution is either x < -4 or -1 ≤ x < 4 or x > 4, which implies (-∞, -4) ⋃ [-1, 4) ⋃ (4, ∞)
![]()
Solve: ${\dfrac{8x+14}{x} <-x-1}$
Solution:
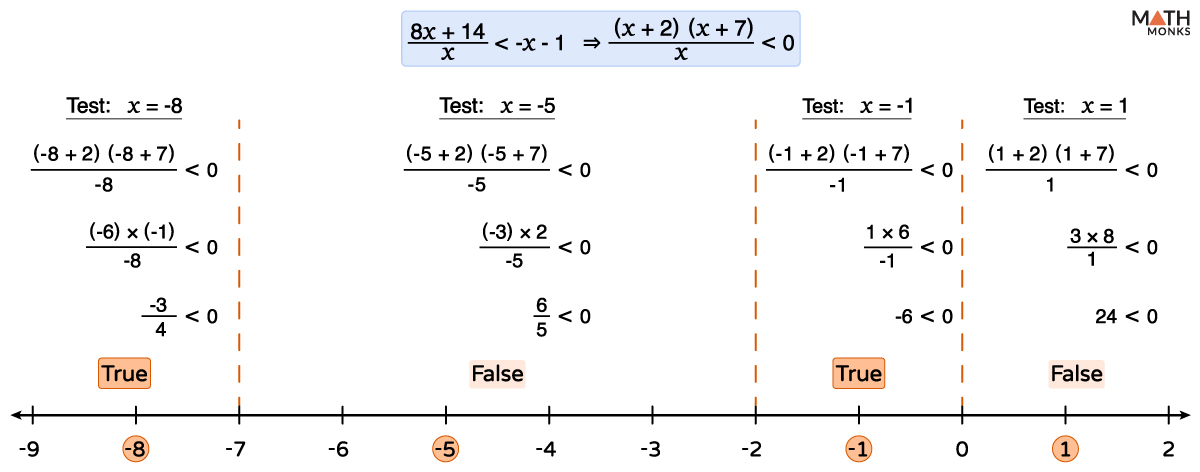
Here, ${\dfrac{8x+14}{x} <-x-1}$
Step 1: Converting into the General form
On adding ‘x’ and 1 to both sides of the inequality, we get
${\dfrac{8x+14}{x}+x+1 <-x-1+x+1}$
⇒ ${\dfrac{8x+14+x^{2}+x}{x} <0}$
Further simplifying, we get
${\dfrac{x^{2}+9x+14}{x} <0}$
⇒ ${\dfrac{\left( x+2\right) \left( x+7\right) }{x} <0}$
Step 2: Finding the Zeros of the Numerator and Denominator
For the numerator and denominator, we get
x + 2 = 0, x + 7 = 0, and x = 0
⇒ x = -2, -7, and 0
Step 3: Dividing the Intervals and Verifying
Now, verifying the intervals between the above critical points on the number line, we get
On verifying the general form of the given inequality at the critical points, we get
At x = -7, ${\dfrac{\left( -7+2\right) \left( -7+7\right) }{-7}=0}$, holds true.
At x = -2, ${\dfrac{\left( -2+2\right) \left( -2+7\right) }{-2}=0}$, holds true.
At x = 0, ${\dfrac{\left( 0+2\right) \left( 0+7\right) }{0}}$, undefined.
Step 4: Determining the Solution
Thus, the solution is either x ≤ -7 or -2 ≤ x < 0
