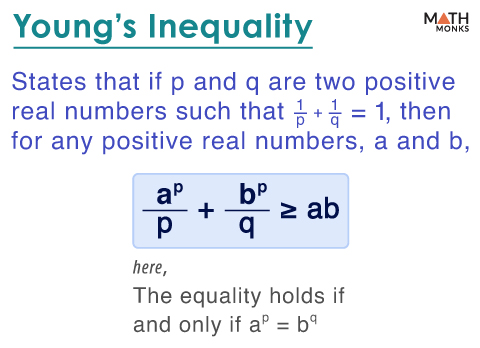Young’s Inequality

Young’s inequality states that if ‘p’ and ‘q’ are positive real numbers satisfying ${\dfrac{1}{p}+\dfrac{1}{q}=1}$, then for another set of positive real numbers, ‘a’ and ‘b,’

${ab\leq \dfrac{a^{p}}{p}+\dfrac{b^{q}}{q}}$, here the equality holds if and only if a^p = b^q

This is the generalized form of Young’s inequality.

Proof

Using Weighted AM-GM Inequality

Let ${w_{1}=\dfrac{1}{p}}$ and ${w_{2}=\dfrac{1}{q}}$

Now, the weighted AM-GM inequality is written as,

${\dfrac{w_{1}a^{p}+w_{2}b^{q}}{w_{1}+w_{2}}\geq \left( \left( a^{p}\right) ^{w_{1}}\left( b^{q}\right) ^{w_{2}}\right) ^{\dfrac{1}{w_{1}+w_{2}}}}$ …..(i)

Since ${\dfrac{1}{p}+\dfrac{1}{q}=1}$ ⇒ w₁ + w₂ = 1

Thus, from (i), ${\dfrac{a^{p}}{p}+\dfrac{b^{q}}{q}\geq \left( a^{p}\right) ^{\dfrac{1}{p}}\left( b^{q}\right) ^{\dfrac{1}{q}}}$

⇒ ${\dfrac{a^{p}}{p}+\dfrac{b^{q}}{q}\geq ab}$ with the equality if and only if a^p = b^q, which proves Young’s inequality.

Using Logarithms

Let us consider the function f(x) = ln(x) and a, b > 0

Now, for all positive x, y, and t Є (0, 1),

ln(tx + (1 – t)y) ≥ t ln(x) + (1 – t) ln(y) with the equality if and only if x = y

By considering x = a^p, y = b^q, t = ${\dfrac{1}{p}}$, and (1 – t) = ${1-\dfrac{1}{p}=\dfrac{1}{q}}$, we get

${\ln \left( \dfrac{a^{p}}{p}+\dfrac{b^{q}}{q}\right) \geq \dfrac{1}{p}\ln \left( a^{p}\right) +\dfrac{1}{q}\ln \left( b^{q}\right)}$

⇒ ${\ln \left( \dfrac{a^{p}}{p}+\dfrac{b^{q}}{q}\right) \geq \dfrac{p}{p}\ln \left( a\right) +\dfrac{q}{q}\ln \left( b\right)}$

⇒ ${\ln \left( \dfrac{a^{p}}{p}+\dfrac{b^{q}}{q}\right) \geq \ln \left( a\right) +\ln \left( b\right)}$

⇒ ${\ln \left( \dfrac{a^{p}}{p}+\dfrac{b^{a}}{q}\right) \geq \ln \left( ab\right)}$

Now, exponentiating both sides, we get

${\dfrac{a^{p}}{p}+\dfrac{b^{q}}{q}\geq ab}$ with the equality if and only if a^p = b^q, which again proves Young’s inequality. 

For Products

Young’s inequality for increasing functions (a special case of Young’s inequality for products) states that if f(x) is a continuous and increasing function defined for positive real numbers x, with f(0) = 0, and the positive real numbers ‘a’ is the domain and ‘b’ is the image of ‘f,’ then 

${ab\leq \int ^{a}_{0}f\left( x\right) dx+\int ^{b}_{0}f^{-1}\left( x\right) dx}$, with the equality if and only if the function f(a) = b

Proof

Let us consider the function g(a) with the expression 

${g\left( a\right) =ab-\int ^{a}_{0}f\left( x\right) dx}$, where the parameter b > 0 …..(i)

Since g’(a) = b – f(a) and the function ‘f’ is increasing, then

g’(a) > 0, for 0 < a < f^-1(b)

g’(a) = 0, for a = f^-1(b)

g’(a) < 0, for a > f^-1(b)

From the above, g(a) is the maximum value of the function ‘g’ attained at a = f^-1(b)

Thus, g(a) ≤ max g(x) = g(f^-1(b)) …..(ii)

Integrating R.H.S. of (ii) partially, we get

${g\left( f^{-1}\left( b\right) \right) =bf^{-1}\left( b\right) -\int ^{f^{-1}\left( b\right) }_{0}f\left( x\right) dx}$

⇒ ${g\left( f^{-1}\left( b\right) \right) =\int ^{f^{-1}\left( b\right) }_{0}xf’\left( x\right) dx}$

Now, considering y = f(x), we get

${g\left( f^{-1}\left( b\right) \right) =\int ^{b}_{0}f^{-1}\left( y\right) dy}$ …..(iii)

Combining (i), (ii), and (iii), we get

${ab-\int ^{a}_{0}f\left( x\right) dx\leq \int ^{b}_{0}f^{-1}\left( y\right) dy}$

⇒ ${\int ^{a}_{0}f\left( x\right) dx+\int ^{b}_{0}f^{-1}\left( y\right) dy\geq ab}$ …..(iv)

From (iv), we get

${\int ^{a}_{0}f\left( x\right) dx+\int ^{b}_{0}f^{-1}\left( x\right) dx\geq ab}$

Thus, Young’s inequality is proved.

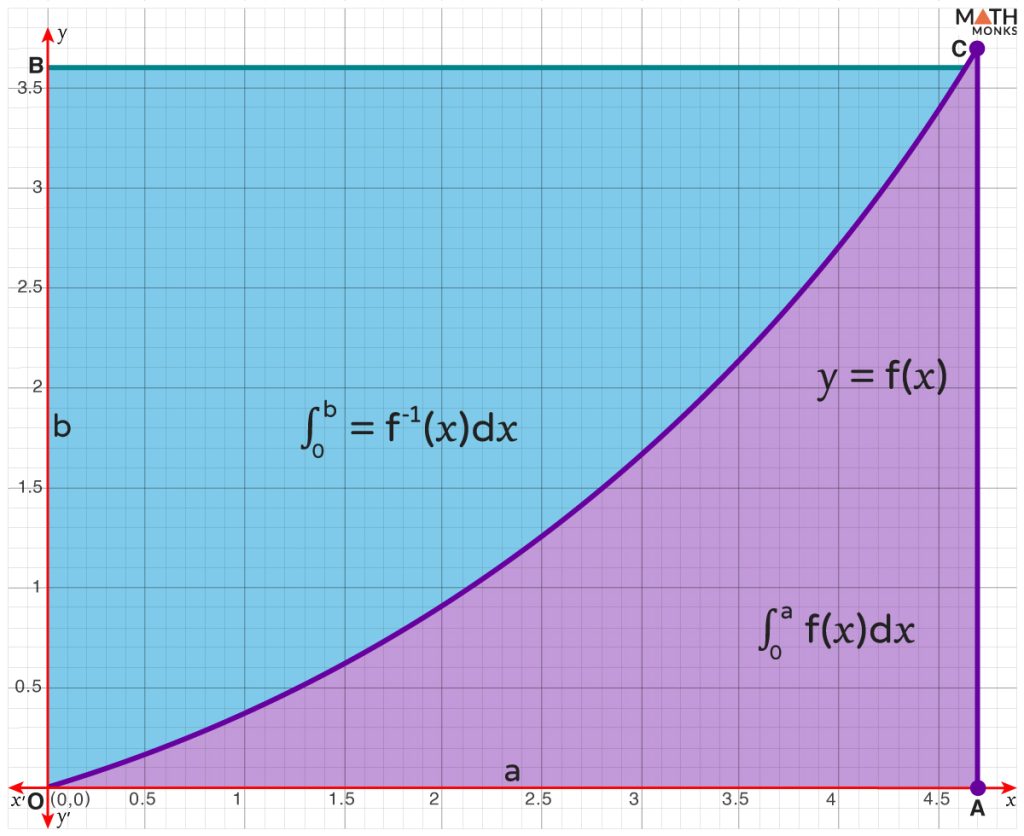
Geometric Interpretation

On representing geometrically,

Here, the area of the curved triangle OAC is ${\int ^{a}_{0}f\left( x\right) dx}$ and the area of the curved triangle OBC is ${\int ^{b}_{0}f^{-1}\left( x\right) dx}$. The shaded region expresses the inequality, and the equality holds if there is no extra area (when b = a).