The standard form, also known as the general form of a linear equation, is one of the three ways in which we can express linear equations. The other two are the slope-intercept form and the point-slope form.
The standard form of linear equation in one variable is given by:
Ax + B = 0
The standard form of linear equation in two variables is given by:
Ax + By = C
Here,
- A, B, and C are the integers, where A is a positive integer
- x and y are variables
Here is an example of a linear equation in the standard form:
7x – 3y = 16
Here, A = 7, B = -3, and C = 16 (all are integers), and A > 0.
The standard form of a linear equation is used in solving systems of equations, where the equations are arranged one above the other for further simplification. It clearly shows the relationship between the variables.
These equations are also used for graphing by first converting to the slope-intercept form.
Converting to Standard Form
The slope-intercept form is expressed as y = mx + b, and the point-slope form is expressed as (y – y1) = m(x – x1).
From Slope-Intercept Form
Let us convert the equation ${y=\dfrac{2}{3}x-4}$ to its standard form.
Step 1: Simplifying
Multiplying both sides by 3 to eliminate the fraction,
⇒ 3y = 2x – 12
Step 2: Moving the Variable Terms to One Side
If the linear equation is already in simplified form, we rewrite the terms to match the standard form of the linear equation.
⇒ 3y – 2x = -12
⇒ -2x + 3y = -12
Step 3: Rearranging the Terms
Since A is negative, we multiply the equation by -1 to make it positive.
⇒ 2x – 3y = 12
This is the standard form of the given equation.
From Point-Slope Form
Let us convert the equation ${y-4=\dfrac{1}{2}\left( x-6\right)}$ to its corresponding standard form.
Step 1: Simplifying
Multiplying both sides by 2 to eliminate the fraction,
⇒ 2(y – 4) = x – 6
⇒ 2y – 8 = x – 6
Step 2: Moving the Variable Terms to One Side
Now, by making the left-hand side of the equation the same as the standard form,
⇒ 2y – x = -6 + 8
⇒ -x + 2y = 2
Step 3: Rearranging the Terms
Since A is negative, we multiply the equation by -1 to make it positive.
⇒ x – 2y = -2
This is the standard form of the given equation.
Graphing
To graph an equation from its standard form, we first need to find its x- and y-intercepts. These points show where the line crosses the x-axis and y-axis, respectively.
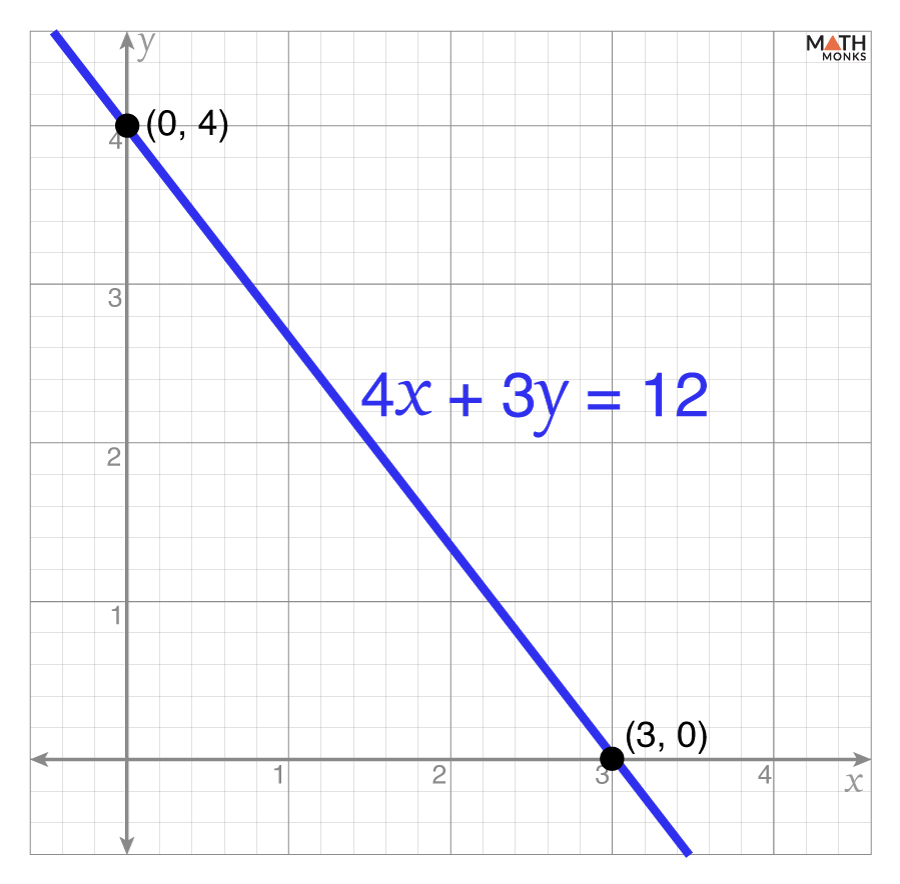
Let us graph the equation: 4x + 3y = 12
Step 1: Finding the X-Intercept
Since at the x-intercept, y = 0
Now, substituting y = 0 into the equation, we get
4x + 3y = 12
⇒ 4x + 3(0) = 12
⇒ 4x = 12
Solving for x, we get
⇒ x = 3
Thus, the x-intercept is (3, 0)
Step 2: Finding the Y-Intercept
Since at the y-intercept, x = 0
Now, substituting x = 0 into the equation, we get
4x + 3y = 12
⇒ 4(0) + 3y = 12
⇒ 3y = 12
Solving for y, we get
⇒ y = 4
Thus, the y-intercept is (0, 4)
Step 3: Plotting the Intercepts and Drawing the line
When plotting the points (3, 0) and (0, 4) on the graph, we get
Here, the line represents the equation 4x + 3y = 12, and every point on it is a solution to the equation.
Solved Examples
![]() Convert the equation ${y=\dfrac{5}{2}x-\dfrac{7}{3}}$ into standard form.
Convert the equation ${y=\dfrac{5}{2}x-\dfrac{7}{3}}$ into standard form.
Solution:
![]()
Given, ${y=\dfrac{5}{2}x-\dfrac{7}{3}}$
Step 1: Simplifying
Adding the fractions on the right-hand side, we get
⇒ ${y=\dfrac{15x-14}{6}}$
Cross-multiplying,
⇒ 6y = 15x – 14
Step 2: Moving the Variable Terms to One Side
⇒ 6y – 15x = -14
⇒ -15x + 6y = -14
Step 3: Rearranging the Terms
⇒ 15x – 6y = 14
Thus, the linear equation in the standard form is: 15x – 6y = 14
![]() Find the x- and y-intercepts of the equation 5x – 2y = 10
Find the x- and y-intercepts of the equation 5x – 2y = 10
Solution:
![]()
Given, 5x – 2y = 10 …..(i)
Substituting y = 0 in equation (i),
⇒ 5x – 2(0) = 10
⇒ 5x = 10
⇒ x = 2
Thus, the x-intercept is (2, 0)
Substituting x = 0 in equation (i),
⇒ 5(0) – 2y = 10
⇒ -2y = 10
⇒ -y = 5
⇒ y = -5
Thus, the y-intercept is (0, -5)
![]() Graph the equation 2x + 3y = 6 using x- and y-intercepts.
Graph the equation 2x + 3y = 6 using x- and y-intercepts.
Solution:
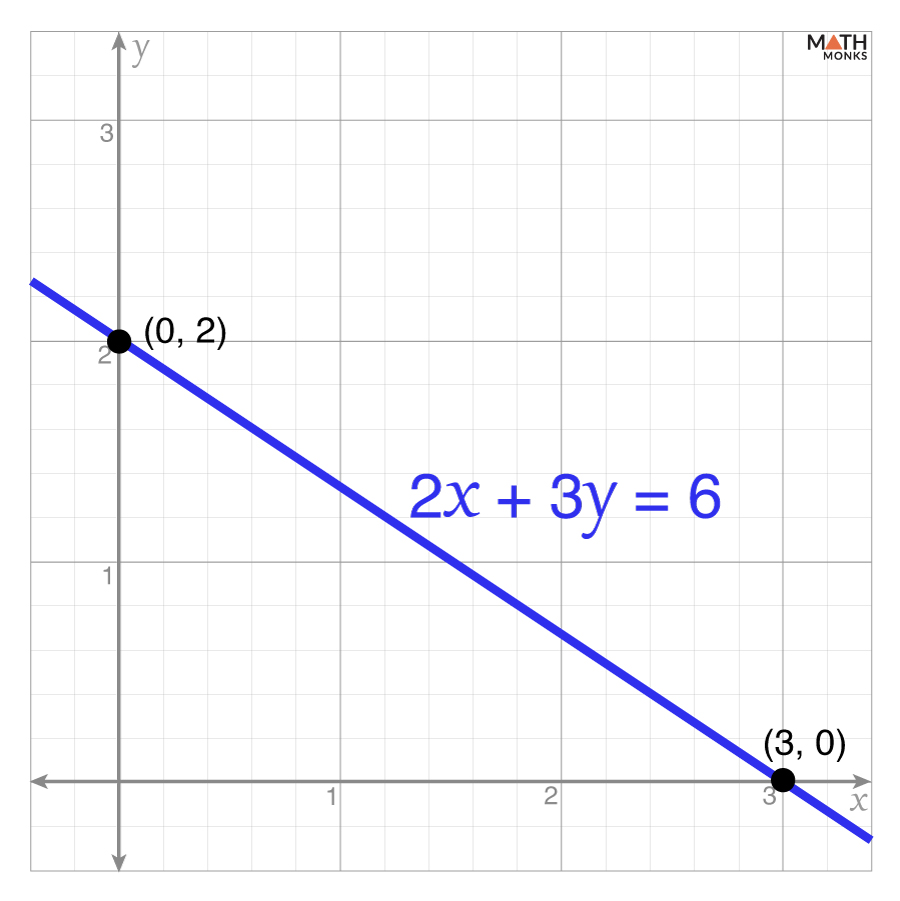
Given, 2x + 3y = 6
Substituting y = 0,
2x + 3(0) = 6
⇒ 2x = 6
⇒ x = 3
Thus, the x-intercept is (3, 0)
Substituting x = 0,
2(0) + 3y = 6
⇒ 3y = 6
⇒ y = 2
Thus, the y-intercept is (0, 2)
When plotting these points, we get the required graph.
![]() Find the standard form equation of a line with a slope of ${\dfrac{3}{4}}$ and a y-intercept of -2.
Find the standard form equation of a line with a slope of ${\dfrac{3}{4}}$ and a y-intercept of -2.
Solution:
![]()
As we know, the equation of a line in the slope-intercept form is given by:
y = mx + c
Here,
m = slope = ${\dfrac{3}{4}}$
c = y-intercept = -2
Thus, the linear equation is: y = ${\dfrac{3}{4}x-2}$
Now, simplifying further, we get
y = ${\dfrac{3x-8}{4}}$
⇒ 4y = 3x – 8
⇒ -3x + 4y = -8
⇒ 3x – 4y = 8
Thus, the standard form of the line is: 3x – 4y = 8