Antilogarithms

Antilogarithm (in short, antilog) is the inverse operation of the logarithm. The logarithm takes a number and returns the exponent to which the base is raised to obtain that number, while the antilogarithm takes an exponent and raises the base to it. 

Mathematically, if log_bx = y, then b^y = x and antilog_b(y) = x

For example, as the logarithm (base 10) of 100 is 2, the antilogarithm of 2 is antilog(2) = 100.

While computing the natural log’s antilogarithm, we raise ‘e’ to that power. For example, if ln1 = 0, then e⁰ = 1, and thus, the antilogarithm (base e) of 0 is antilog_e(0) = 1.

Finding

Using the Antilogarithm Table

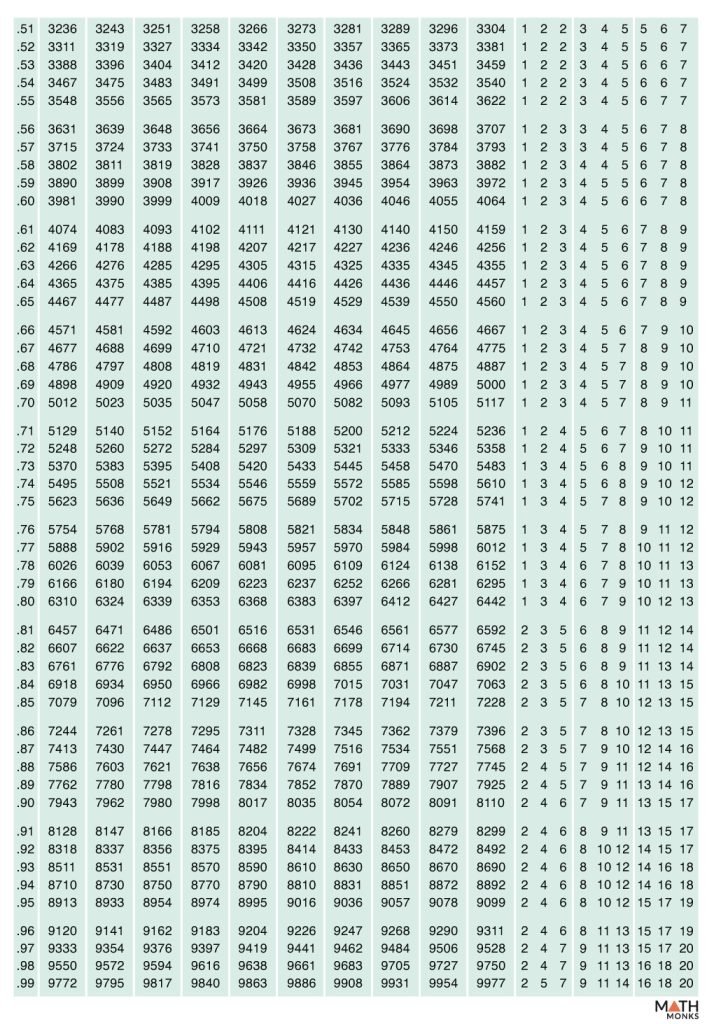
We can use the antilog of a number easily using a scientific calculator. However, if we are not provided a calculator, we can find the antilogarithm values of a positive or a negative number using the antilog table given below. 

The antilog table is divided into three blocks:

1. The first block is the main column (the first column) with numbers from 0.00 to 0.99
2. The second block (the differences columns) with digits 0 to 9
3. The third block (the mean differences columns) with digits 1 to 9

Now, using the antilog table, let us find the antilogarithm value (base 10) of the number 2.3924.

Step 1: Separating the characteristic part (the integer part) and the mantissa part (the decimal part), we get:

Characteristic part = 2 and mantissa part = 0.3924

Step 2: Now, let us find the corresponding value of the mantissa part 0.3924 from the antilog table.

The corresponding difference value in row number 2, which starts with 0.39, is 2466.

Step 3: The corresponding mean difference value in row number 4, starting with 0.39,  is 2.

Step 4: Adding the obtained values, we get 2466 + 2 = 2468

Step 5: The decimal point is placed in the position obtained by adding 1 to the characteristic part. Here, on adding 1 to the characteristic part 2, we get 1 + 2 = 3

Thus, by adding the decimal point after 3 digits from the left, we get 246.8

Thus, the antilog of 2.3924 is 246.8

Without Using the Antilogarithm Table

Now, let us find the antilog of 2.3924

Here, the characteristic part = 2, and the mantissa part = 0.3924

Thus, antilog(2.3924) = 10² × 10^0.3924

Since, 10^0.3924 ≈ 2.468

⇒ antilog(2.3924) = 100 × 2.468

⇒ antilog(2.3924) = 246.8

Solved Examples