Derivatives of Logarithmic Functions

Finding the derivative of any logarithmic function is called logarithmic differentiation.  

The derivative of the natural logarithmic function (with the base ‘e’), lnx, with respect to ‘x,’ is ${\dfrac{1}{x}}$ and is given by 

${\dfrac{d}{dx}\left( \ln x\right) =\left( \ln x\right)’=\dfrac{1}{x}}$, where x > 0

Similarly, the derivative of the logarithmic functions to the base ‘b,’ log_bx, with respect to ‘x,’ called the common logarithm ${\dfrac{1}{x\ln b}}$ is represented by

${\dfrac{d}{dx}\left( \log _{b}x\right) =\left( \log _{b}x\right)’=\dfrac{1}{x\ln b}}$, where x > 0 and ‘b’ is any positive real number except 1 (b Є ℝ⁺ and b ≠ 1)

Proof of the Natural Logarithmic Function

To prove the derivative of the natural logarithmic function, we use the implicit differentiation of its inverse, also known as the exponential form.

Let us assume y = lnx = log_ex.

Converting it into its exponential form, we get

e^y = x

Now, by differentiating both sides with respect to x, we get

${\dfrac{d}{dx}\left( e^{y}\right) =\dfrac{d}{dx}\left( x\right)}$

⇒ ${\dfrac{d}{dx}\left( e^{y}\right) =1}$

⇒ ${e^{y}\ln e\dfrac{dy}{dx}=1}$

Since e^y = x, we have

${x\ln e\dfrac{dy}{dx}=1}$

⇒ ${\dfrac{dy}{dx}=\dfrac{1}{x\ln e}}$

Since lne = 1, ${\dfrac{dy}{dx}=\dfrac{1}{x}}$

Mathematically, if h(x) = ln(f(x)), then for all values of x, f(x) > 0, and 

${h’\left( x\right) =\dfrac{f’\left( x\right) }{f\left( x\right)}}$

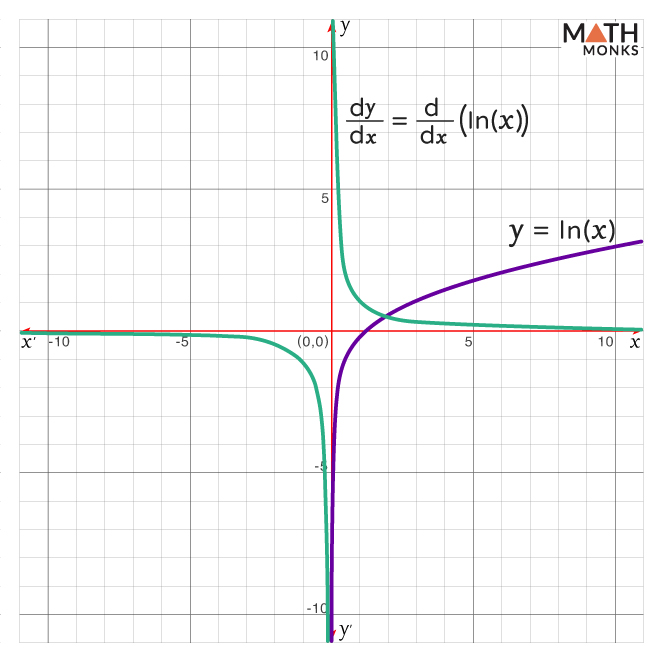
Representing Graphically

The graph of y = log_ex = lnx and its derivative ${\dfrac{dy}{dx}=\dfrac{1}{x}}$ are shown below.

Proof of the Common Logarithmic Function

To prove the common logarithmic function’s derivative, we use implicit differentiation similar to that used to prove the natural logarithmic function’s derivative.

Let us assume a logarithmic function y = log_bx

Converting it into its exponential form, we get

b^y = x

Now, by differentiating both sides with respect to x, we get

${\dfrac{d}{dx}\left( b^{y}\right) =\dfrac{d}{dx}\left( x\right)}$

⇒ ${\dfrac{d}{dx}\left( b^{y}\right) =1}$

⇒ ${b^{y}\ln b\dfrac{dy}{dx}=1}$

Since b^y = x, we have

${x\ln b\dfrac{dy}{dx}=1}$

⇒ ${\dfrac{dy}{dx}=\dfrac{1}{x\ln b}}$

Mathematically, if h(x) = log_b(f(x)), then for all values of x, f(x) > 0, and 

${h’\left( x\right) =\dfrac{f’\left( x\right) }{f\left( x\right) \ln b}}$

Alternative Method

We can also obtain the derivative formula of the common logarithmic function by using ${\dfrac{d}{dx}\left( \ln x\right) =\dfrac{1}{x}}$

Let us verify this by considering the function f(x) = log_bx.

Now, by changing the base rule, we get

${\log _{b}x=\dfrac{\log _{e}x}{\log _{e}b}}$

Since logₑ = ln, f(x) = ${\dfrac{\ln x}{\ln b}}$

Differentiating both sides with respect to x, we get

${f’\left( x\right) =\dfrac{d}{dx}\left( \dfrac{\ln x}{\ln b}\right)}$

⇒ ${f’\left( x\right) =\left( \dfrac{1}{\ln b}\right) \dfrac{d}{dx}\left( \ln x\right)}$

⇒ ${f’\left( x\right) =\left( \dfrac{1}{\ln b}\right) \left( \dfrac{1}{x}\right)}$

⇒ ${\dfrac{d}{dx}\left( \log _{b}x\right) =\dfrac{1}{x\ln b}}$

Thus, the derivative of log_bx with respect to x is ${\dfrac{1}{x\ln b}}$, proved.

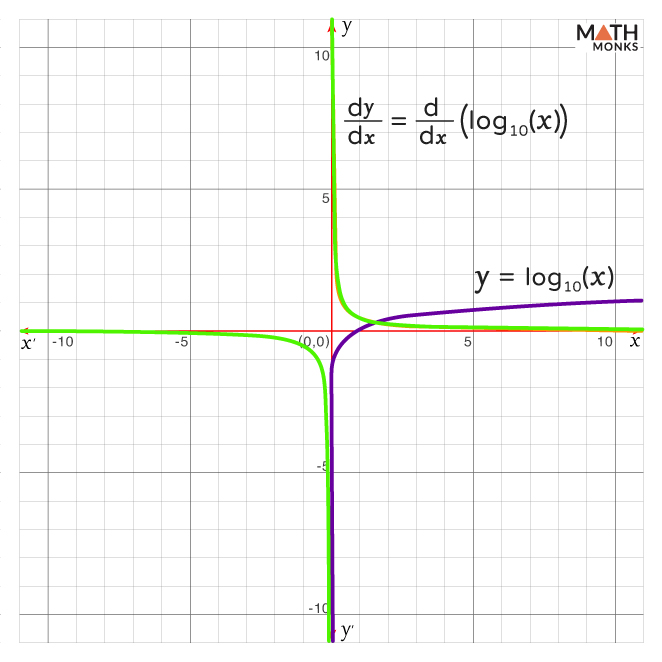
Representing Graphically

The graph of y = log₁₀x = logx and its derivative ${\dfrac{dy}{dx}=\dfrac{1}{x\ln 10}}$ are shown below.