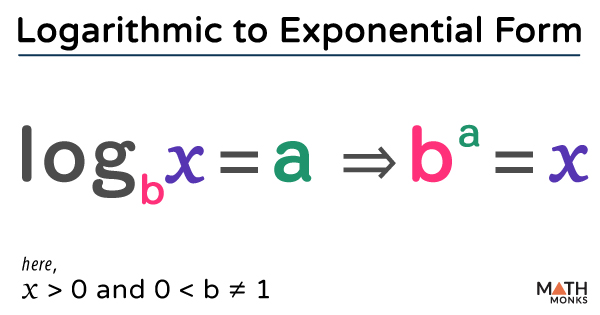Logarithm is the exact opposite of exponentiation. A number written in the exponent form is much easier to interpret than when it is expressed in the logarithmic form.
In mathematical calculations, we frequently convert a given logarithmic equation to its corresponding exponential form.
For example, 33 = 27 is much easier to understand compared to the form log3(27) = 3
Formula
The relationship between logarithmic and exponential forms can be represented by the formula:
If logbx = a, then ba = x, for all x > 0 and 0 < b ≠ 1
Here, b = base, a = exponent, and x is the result.
Steps
Let us convert the logarithmic representation of log8(512) = 3 in its exponential form.
Step 1: Identifying the Base, Exponent, and Argument
Here,
Base = 8
Exponent = 3
Argument = 12
Step 2: Using the Formula
83 = 512
Thus, log8(512) = 3 in its exponential form is 83 = 512
Converting Natural Logarithms
The natural logarithm y = ln(x) or y = loge(x) can also be converted to its exponential form as:
If y = ln(x) or y = loge(x), then ey = x for all x > 0.
For example, the exponential form of the natural logarithm y = ln(4.5) ≈ 1.504 is e1.504 ≈ 4.5
Solved Examples
![]()
Find the value of log225 and convert it into its exponential form (Given: log5 = 0.699 and log3 = 0.477)
Solution:
![]()
As we know, log5 = 0.699 and log3 = 0.477
Here, log225
= log(52 ⋅ 32)
= log(52) + log(32) (by the product rule of logarithm)
= 2 log5 + 2 log 3 (by the power rule of the logarithm)
= 2 × 0.699 + 2 × 0.477
= 1.398 + 0.954
= 2.352
Thus, log225 = 2.352
⇒ 102.352 = 224.905, the required exponential form.
![]()
Convert log7(2401) = 4 into its exponential form.
Solution:
![]()
As we know, If logbx = a, then ba = x
Here, log7(2401) = 4
⇒ 74 = 2401Thus, the exponential form is 74 = 2401
