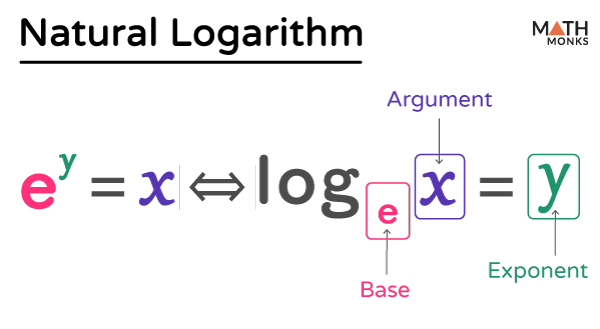
The natural logarithm (base-e-logarithm) of a positive real number x, represented by lnx or logex, is the exponent to which the base ‘e’ (≈ 2.718…, Euler’s number) is raised to obtain ‘x.’
Mathematically, ln(x) = loge(x) = y if and only if ey = x
It is also written as:
${\ln x=\int ^{x}_{1}\dfrac{1}{t}dt}$
The number 2.718… is used naturally in math and science calculations, like pie (π) in geometry.
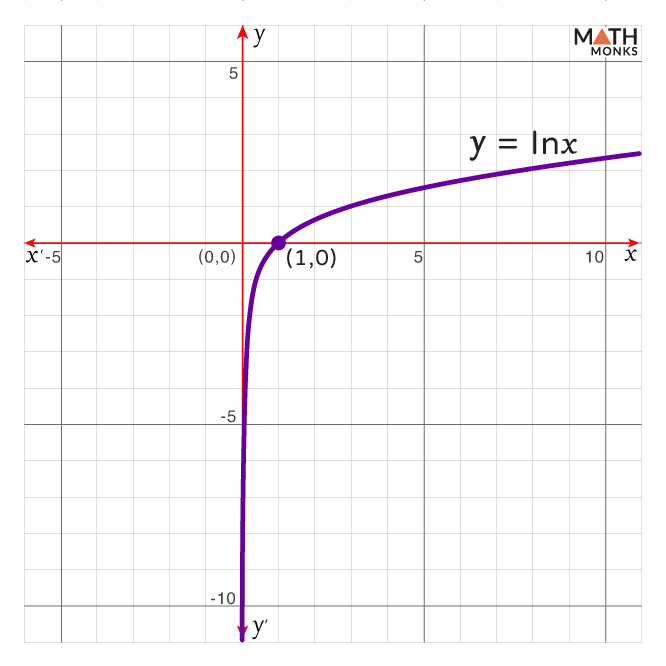
Graphing
The geometric interpretation of the natural logarithmic function y = lnx is shown below.
Here, the natural logarithmic function has an asymptote at x = 0 and an x-intercept at (1, 0).
Proof
Now, let us verify the natural logarithm formula ${\ln x=\int ^{x}_{1}\dfrac{1}{t}dt}$
According to the fundamental theorem of calculus, if F(x) is an antiderivative of f(x) for the interval [a, b], then ${\int ^{b}_{a}f\left( x\right) dx=f\left( b\right) -f\left( a\right)}$
Now, let us find an antiderivative of ${f\left( t\right) =\dfrac{1}{t}}$
${\int \dfrac{1}{t}dt=\ln \left| t\right| +C}$, here c is the integrating constant.
Applying the fundamental theorem of calculus, we get
${\int ^{x}_{1}\dfrac{1}{t}dt=\ln \left| x\right| -\ln \left| 1\right|}$
= ${\ln \left| x\right| -0}$
= ${\ln \left| x\right|}$
Thus, ${\int ^{x}_{1}\dfrac{1}{t}dt=\ln \left| x\right|}$, is proved.
Rules
The natural logarithm follows all the properties of the logarithm.
Product Rule
ln(xy) = lnx + lny
Example: ln(10) = ln(5) + ln(2)
Quotient Rule
${\ln \left( \dfrac{x}{y}\right) =\ln x-\ln y}$
Example: ${\ln \left( \dfrac{42}{5}\right) =\ln 42-\ln 5}$
Power Rule
ln(xn) = n lnx
Example: ln((5z)7) = 7 ln(5z)
Change of Base Rule
${\ln x=\log _{e}x=\dfrac{\log _{b}x}{\log _{b}e}}$
Or, lnx ⋅ logbe = logbx
Example: ${\ln \left( 2p^{2}\right) =\log _{e}\left( 2p^{2}\right) =\dfrac{\log _{b}\left( 2p^{2}\right) }{\log _{b}e}}$, for any base b
Identity Rule
ln(e) = 1
Zero Rule
ln(1) = 0
Infinity Rule
ln(∞) = ∞, which means while the argument ‘x’ approaches to infinity, the limit of ln(x) is:
lim ln(x) = ∞, when x → ∞
Derivative Rule
${\dfrac{d}{dx}\left( \ln \left( x\right) \right) =\dfrac{1}{x}}$
Integration Rule
${\int \ln \left( x\right) dx=x\left( \ln \left( x\right) -1\right) +c}$
Others
- ln of Negative Numbers: ln of any negative number is undefined.
- ln of ‘0’ and the Limit: ln(0) is undefined, which means while the argument ‘x’ approaches zero, the limit of ln(0) is minus infinity. That is, lim ln(0) = -∞, when x → 0+
- ln of ‘e’ raised to the power ‘x’: ln(ex) = x
- ‘e’ raised to the ln power: eln(x) = x
Solved Example
![]() Simplify: ln(e4x) + 4ln(x) – 2ln(2x)
Simplify: ln(e4x) + 4ln(x) – 2ln(2x)
Solution:
![]()
Here, ln(e4x) + 4ln(x) – 2ln(2x)
= 4x ln(e) + ln(x4) – ln((2x)2) (by the power rule of logarithm)
= 4x + ln(x4) – ln(4x2) (since ln(e) = 1)
= ${4x+\ln \left( \dfrac{x^{4}}{4x^{2}}\right)}$ (by the quotient rule of logarithm)
= ${4x+\ln \left( \dfrac{x^{2}}{4}\right)}$
= ${4x+\ln \left( \left( \dfrac{x}{2}\right) ^{2}\right)}$
= ${4x+2\ln \left( \dfrac{x}{2}\right)}$ (by the power rule of logarithm)
Thus, ln(e4x) + 4ln(x) – 2ln(2x) = ${4x+2\ln \left( \dfrac{x}{2}\right)}$
![]() Convert the natural logarithmic equation ln(15) = 2.708 (corrected to 3 decimal places) into its exponential form.
Convert the natural logarithmic equation ln(15) = 2.708 (corrected to 3 decimal places) into its exponential form.
Solution:
![]()
As we know, ln(x) = y ⇔ ey = x
Here, ln(15) = 2.708Thus, e2.708 = 15